9.8 批量归一化

批量归一化（Batch Normalization）是一种在深度学习里常用的技术，它可以让深度神经网络的训练更稳定，收敛更快。

9.8.1 批量归一化的动机

之前我们讲过对输入数据做归一化的好处，它可以让训练更加稳定，收敛更快。我们对输入的数据进行了归一化，它让不同的特征取值范围都是相似的，但是随着网络的前向传播，网络深处层的输入取值范围又会被逐渐拉大。这让更新这些层的参数变得不稳定。

那我们是否可以对神经网络的每一层的输出（下一层的输入）进行归一化呢？这就是批量归一化的动机。

9.8.2 具体实现

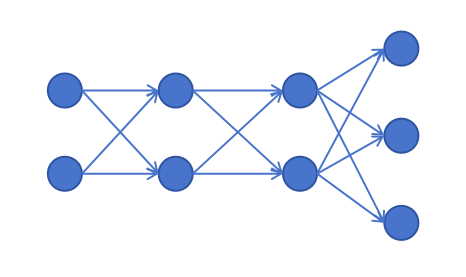对于上边的网络结构，输入层有2个feature，第一个层有2个神经元。对于第一层的这两个神经元，在经过激活前，有两个z值， $z_1^1,z_2^1$ ，经过激活后，也有两个a值 $a_1^1,a_2^1$ 。批量归一化可以对激活前的z值进行归一化，也可以对激活后的a值进行归一化。一般情况下我们是对激活前的z值进行归一化。

另外我们训练时是按照mini-batch进行训练的，每次得到的z值也是一个batch的。比如batch size为512，对于第一层的 $z_1^1,z_2^1$ 。这两个z值分别在每个batch的512个数据上计算均值 $\mu$ 和标准差 $\sigma$ ，然后进行标准化。

以 $z_1^1$ 为例，具体计算公式如下，其中 $i$ 表示第 $i$ 个样本 $z_1^1$ 的值， $\epsilon$ 是为了防止除0，加的一个很小的数。

$(z_1^1)_{norm}^i=\frac{(z_1^1)^i-\mu_1^1}{\sigma_1^1+\epsilon}$

接下来，还需要对 ${(z_1^1)}_{norm}$ 进行一个线性变化，才得到最终的Batch Norm后的结果。

${(z_1^1)}_{BN}=\gamma_1^1 {(z_1^1)}_{norm}+\beta_1^1$

其中的 $\gamma,\beta$ 都和权重一样是可以学习的参数。会在模型训练中进行更新。

对于 ${(z_1^1)}$ 而言，如果：

$\gamma_1^1=\sigma_1^1+\epsilon$

$\beta_1^1=\mu_1^1$

那么 $(z_1^1)_{BN}=z_1^1$ 可以看到如果模型是有可能通过学习调整 $\gamma,\beta$ 的值，让批量归一化后的值等于原始值的。但是，初始化时，一般设置 $\gamma=1,\beta=0$ 大多数情况下它都限制了输出的均值在零，标准差在1附近。保证了输出分布的稳定性。

因为每个神经元的z值，在进行批量归一化时都要减去这个batch z值的均值，所以就没有必要在计算z值的线性变化里加上偏置项b了，因为不论学到的b是多少，在减去均值后，结果都是一样的。所以如果你对一个线性层后边要加批量归一化，那么这一层就可以不设置偏置项。另外输出层一般不加批量归一化层。

9.8.3 直观理解

我们知道在深度神经网络里，网络浅层学习到的是基本特征，网络深层基于浅层基本特征学到抽象特征，如果没有批量归一化，每一层的输出在训练过程中都一直在变化，这让网络深层刚学到的模式，因为输入的大幅变化又失效了，需要重新学习。而批量归一化可以保证每一层的输出的分布保持稳定的均值和方差，深层网络可以在这个稳固的基础上进行抽象特征的学习。

9.8.4 批量归一化的副作用

虽然批量归一化提出的动机并不是为了正则化，但是在实践中，人们发现批量归一化还有防止模型过拟合的作用。这可能是在批量归一化过程中每次计算的均值和标准差都不一样，数据经过变换后，相当于引入了噪声。这样就让训练的模型更鲁棒，不会过度拟合训练数据。

9.8.5 推理时的批量归一化

在推理时你可以能只有一条数据，那此时该如何获得均值和方差呢？答案是，在训练时，BatchNorm会使用当前batch的z值的均值和标准差进行归一化，并用指数加权平均的办法，更新和维护z值的均值和标准差。在推理时，就用这个指数加权平均得到的均值和标准差来归一化推理时的z值。

9.8.6 PyTorch里添加批量归一化

PyTorch里有定义好的BatchNorm的层，我们需要把它添加在线性变化和激活函数之间就可以了。它需要传入线性变化输出的神经元的个数。具体代码如下：

import torch.nn as nn

class NeuralNetwork(nn.Module):
    def __init__(self):
        super().__init__()
        self.model = nn.Sequential(
            nn.Linear(28 * 28, 128, bias=False),
            nn.BatchNorm1d(128),
            nn.ReLU(),

            nn.Linear(128, 128, bias=False),
            nn.BatchNorm1d(128),
            nn.ReLU(),

            nn.Linear(128, 128, bias=False),
            nn.BatchNorm1d(128),
            nn.ReLU(),

            nn.Linear(128, 64, bias=False),
            nn.BatchNorm1d(64),
            nn.ReLU(),

            nn.Linear(64, 10)
        )

    def forward(self, x):
        return self.model(x)

训练时和推理时的Batch Normalization的操作是不一样的。所以也要记得调用model.train()和model.eval()来切换模型的状态。

model.train()
## 在这里训练你的模型。
model.eval()
## 在这里利用模型进行预测。

批量归一化