15.2 注意力机制

Transformer的论文题目就是《Attention is all you need》，由此可见注意力机制在Transformer里的重要性。

15.2.1 一个比喻

假如你去自助餐厅，拿起一个盘子，准备拿取第一轮的美食。这其中有3个因素，决定了你最终盘子里装了什么。

个人喜好

你是喜欢吃甜食，素食，肉食等等，这是个人喜好，每个人是不一样的。我们是带着个人喜好去寻找食物的，这个我们可以称为“Query”因素。也就是你个人的查找条件。

食物表现

每个食物都有自身的属性，甜食，素食，肉食，色泽，气味等，这些属性用来匹配你的“查找条件”，我们叫做“Key”因素，表示每个食物表现出来的特性。

食物本身

每个食物本身，我们称之为“Value”。

那么人的注意力机制是如何利用Q（Query）、K（Key）、V（Value）来拿取一盘食物呢？你用你的喜好Q，去匹配食物的属性K，计算一个注意力匹配值。根据这个匹配值的大小决定你拿取食物的多少。比如你想吃肉食（Q），这里刚好有个烤羊腿（K），Q和K匹配率很高，也就是说最能吸引你的注意力，那你就回多拿一些羊腿。如果这里有香肠，它虽然也算肉食，但是匹配度不高，吸引你注意力低一些，你就少拿一些。旁边还有一些蔬菜，它和你想吃肉食的Q没有一点匹配，完全吸引不了你的注意力，你就一点蔬菜也不会拿。

这就是注意力机制的核心，它有3个重要的值决定：一个是Q，代表查询变量。一个是K，代表应答变量。一个是V，代表值。Q和K之间计算注意力系数，决定最终取用值的多少。

15.2.2 注意力的计算

我们之前在RNN里讲过注意力机制，那里的注意力机制中的Q就是Decoder当前时间步输入的隐状态。K就是Encoder每个时间步输出的隐状态。V和K一样，都是Encoder每个时间步输出的隐状态。最终计算就是Q和K计算出注意力权值，经过softmax归一化后，按注意力权值对V进行加权求和，就得到了注意力上下文向量了。因为Decoder每个时间步的输入隐状态Q不同，所以最终的注意力上下文也不同。

在之前讲的RNN里计算Q和K的注意力值，是通过将Q向量和K向量进行拼接，然后经过一个神经网络，输出一个值。一个Q和一组K分别计算，得到一组logits值，这一组logits值再经过softmax，就得到这一个Q对这一组K的注意力权重。

在Transformer里，计算Q和K的注意力值用的是一个更简单的办法，就是直接计算Q和K的点乘。当然，计算点乘的前提是Q和K的维度是一致的。一个Q和一组K分别计算点乘，得到一组logits值，再通过softmax，就到的注意力权重。

15.2.3 Transformer里的注意力机制

Transformer原作者是用来解决序列到序列问题的，具体来说，就是解决翻译问题的。

我们之前介绍过对token进行Embedding得到的向量能更好的表示一个token的语义信息，但是同一个token，在不同的上下文语境中它的意思是不同的。 比如下边两句话：

“我爱吃苹果”

“我喜欢苹果手机”

比如上图中，对于“苹果”这个token，我们希望它的Embedding向量值能有所不同，表达出各自不同的含义。

15.2.3.1 自注意力机制

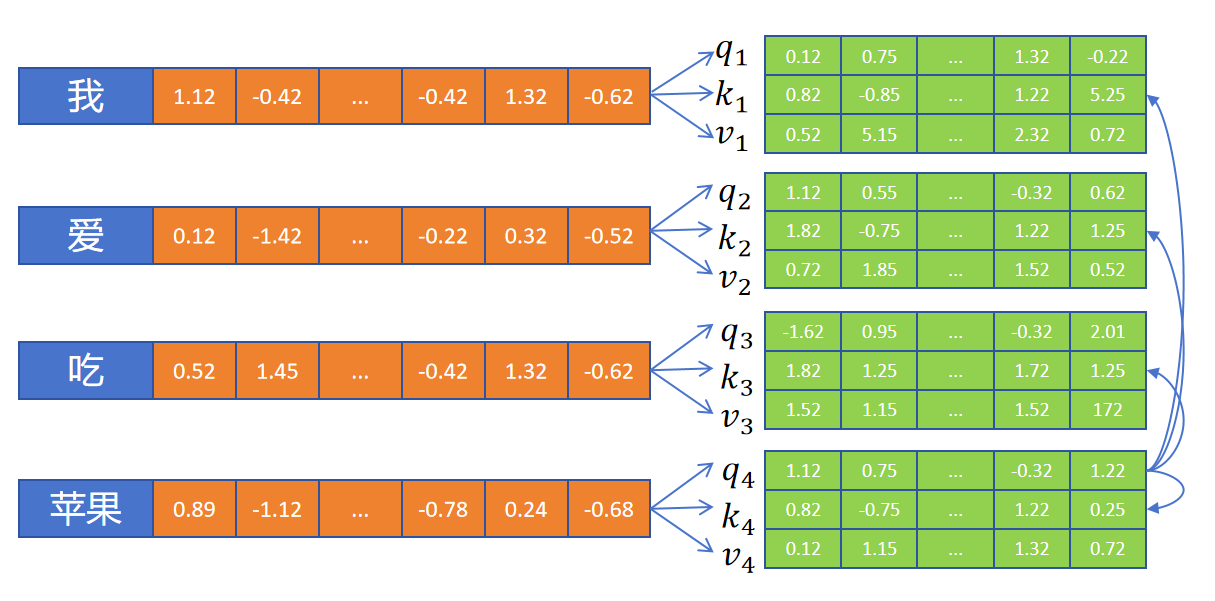如上图所示，首先定义3个全连接层，利用这3个全连接层为每个token生成它们各自的q、k、v向量。全连接层的输入都是当前他们的Embedding。有了q、k、v向量，就可以按照我们上边讲过的方式来进行注意力计算。

苹果这个token，用自己的q向量分别和所有的token（包括自身）的k向量进行点积计算，得到一组值A。

$A = [q_4\cdot k_1, \quad q_4\cdot k_2, \quad q_4\cdot k_3, \quad q_4\cdot k_4]$

然后应用softamx，转化为注意力权重。

$A=softmax(A)=[0.1,0.1,0.3,0.5]$

利用注意力权重，对所有的token的V向量进行加权求和，就得到了苹果这个token根据上下文进行注意力更新后的新的Embedding表示。

$v_4 = 0.1v_1+0.1v_2+0.3v_3+0.5v_4$

因为这里的注意力计算是序列本身内部的token进行的，所以叫做Self-Attention，自注意力。像我们之前讲的RNN里的注意力，是Decoder序列里的Token对Encoder里的Token计算注意力的，是不同序列token之间计算的注意力，那个叫做Cross-Attenion，交叉注意力。

15.2.3.2 多头自注意力

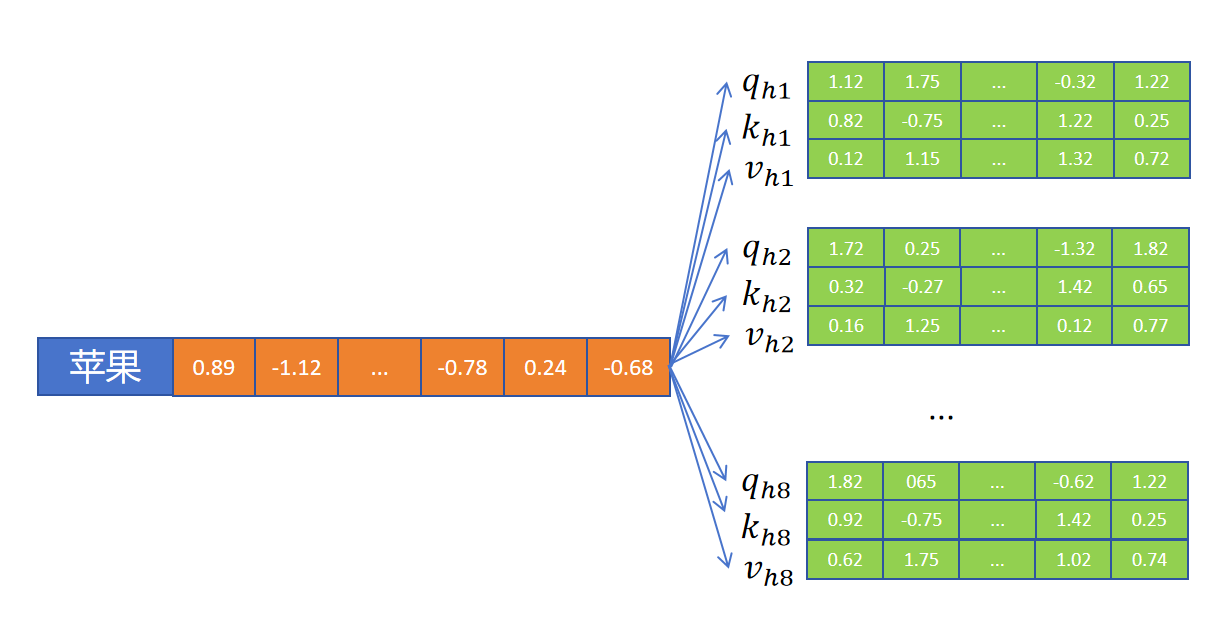在卷积神经网络里，某一层可以定义多个卷积核，每个卷积核来发现不同的特征。注意力机制也可以定义多个，我们把一个注意力计算叫做一个“头”。其中一个“头”负责这个token里的某种特性，比如“单复数”、“性别”、“材质”、“重量”等等。每个头中的q负责查询这个特性，k负责应答这个特性，v提供这个特性的表示值。每个头分别计算自己的注意力权重，并对这个头内部的v加权相加，得到这个头的输出。然后将各个头的输出拼接，就构成了一个token经过多头自注意更新后的Embedding向量了。

为了保证更新前后每个token的Embedding维度不变，假如注意力有N个头，那么每个头的q、k、v的维度就为原始token Embedding维度的1/N。最终N个头进行注意力计算后的输出进行拼接，Embedding的维度就可以保持不变了。

假设“苹果”这个token的Embedding维度为512，8个头，则每个头的q、k、v向量的维度就都为64。每个token的第一个头和序列里其他token的第一个头进行注意力计算，得到一个64维的输出。最终8个头，每个64维的输出，进行拼接，就得到了更新后的512维的Embedding。

15.2.3.3 矩阵运算加速

Transformer的一大优势，就是可以同时更新所有的token的embedding，不用像RNN那样计算每个token的隐状态需要等待序列前边token依次计算出各自的隐状态。我们发现上边讲的注意力机制更新每个token的embedding，所有token是可以同步进行的，没有次序上的依赖关系。 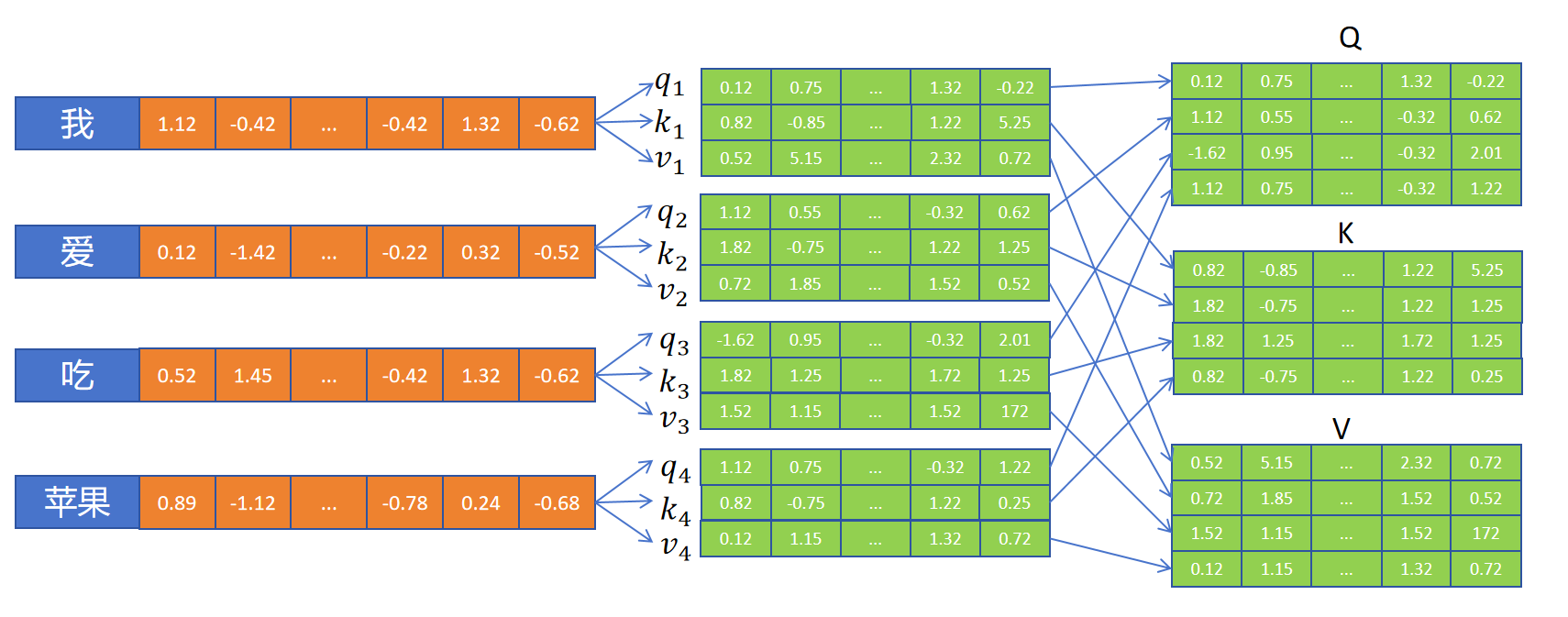更进一步，GPU擅长进行矩阵运算。以一个头的注意力机制为例，也就是q、k、v向量的维度和embedding向量的维度都一样，为hidden_size。所以我们将序列内所有token产生的q向量合并到一起，形成一个Q矩阵，形状为[seq_len,hidden_size]。将所有的k向量合并到一起，形成一个K矩阵，形状为[seq_len,hidden_size]。同理生成V矩阵，形状也为[seq_len,hidden_size]。此时，将Q乘以K的转置相乘：$QK^T$，得到结果形状为[seq_len,seq_len]。其中结果的第一行表示第一个token和序列里每个token注意力的logits的值。第n行的seq_len个值是序列里第n个token和序列所有seq_len个token注意力的logits的值，然后按行应用softmax就得到了注意力权重矩阵。注意力权重矩阵再与V相乘就得到这个注意力层的输出，也就是对序列所有token根据上下文，应用注意力机制更新后的embedding。

$Attention(Q,K,V)=softmax(QK^T)V$

接着我们还要在上边的公式上做一些小的改动，让它更稳定。那就是：

$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$

可以看到，改动是给Q乘以K的转置后的结果先除以$\sqrt{d_k}$，然后再应用softmax。其中$d_k$就是特征维度hidden_size。为什么这里要除以$\sqrt{d_k}$呢？因为特征维度是一个超参数，可以调节，如果特征值分布一致，特征维度越大，那么两个特征向量点乘的值越大，这造成了经过softmax之后，分布很尖锐，注意力大部分都集中在几个token上。其他token的信息就利用不上。假设q、k两个向量维度都为$d_k$，向量内的特征值都是均值为0，方差为1，那么它们两个向量的点积结果，均值为0，方差为$d_k$。所以这里除以标准差$\sqrt{d_k}$，让注意力logits的这一组值也符合均值为0，方差为1的分布。

矩阵运算同样也可以支持多头注意力，我们之前说过为了保证Embedding向量更新前后维度不变，所以对于N个头的多头注意力机制，每个头的q,k,v向量的维度为hidden_size/N。

Transformer在为每个token生成q,k,v向量时，生成的维度和embedding的维度是一致的，然后再按头的个数划分为多个q,k,v，代表每个头的q,k,v。

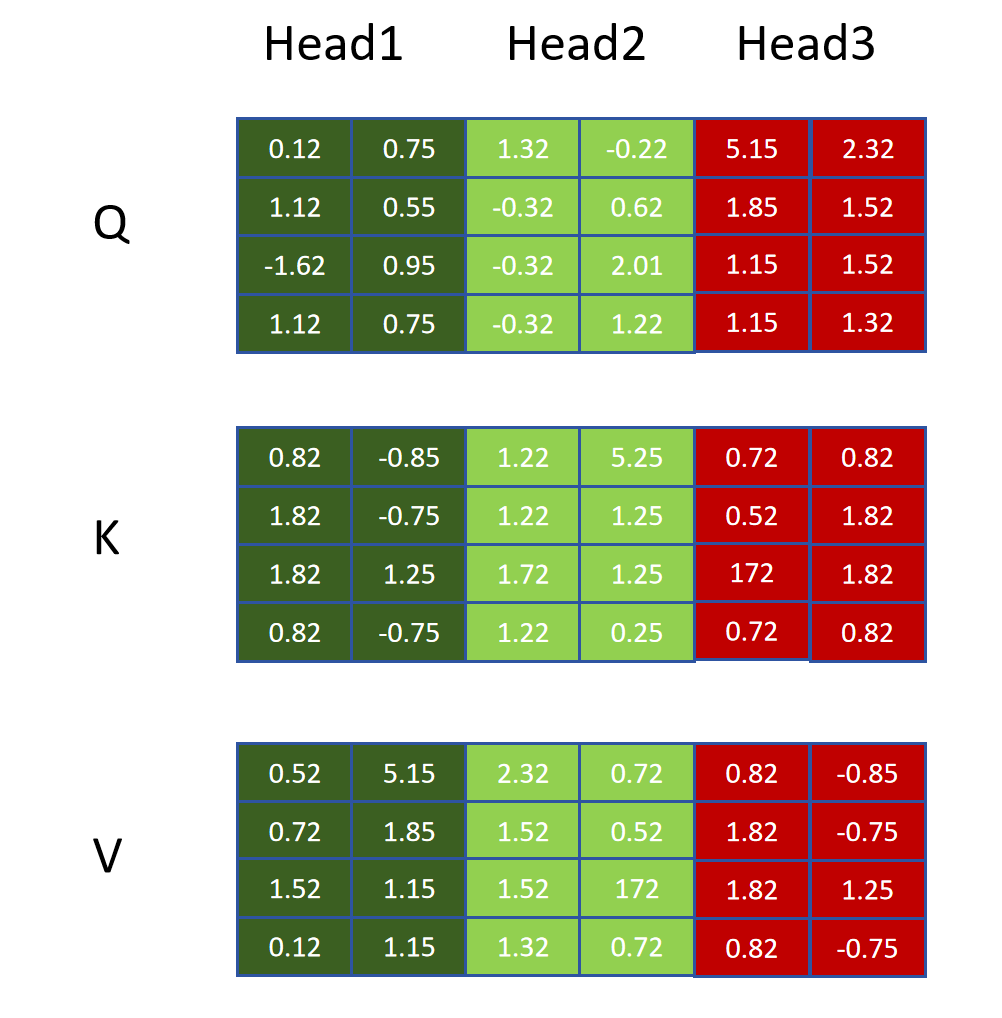
比如上边就是4个token的Q，K，V矩阵，token的hidden_size为6，分了3个头，每个头的q,k,v向量维度为2。整个序列的4个token进行多头注意计算时就是Head1、Head2、Head3的Q,K,V矩阵分别进行计算，分别得到结果矩阵，再将结果矩阵进行拼接，就得到4个token更新后的Embedding。

$Attention(Q,K,V)=concat($

$Attention(Q_{h1},K_{h1},V_{h1}),$

$Attention(Q_{h2},K_{h2},V_{h2}),$

$Attention(Q_{h3},K_{h3},V_{h3})$

$)$

一个完整的注意力机制计算后还会通过一个全连接层来整理token的embedding。这个全连接层不会改变token embedding的维度。

15.2.3.4 pytorch实现

class MultiHeadAttentionBlock(nn.Module):

    def __init__(self, d_model: int, h: int, dropout: float) -> None:
        super().__init__()
        self.d_model = d_model  # embedding特征大小
        self.h = h  # 头的个数
        # 确保d_model可以被h整除
        assert d_model % h == 0, "d_model 不能被 h整除"

        self.d_k = d_model // h  # 每个头特征大小
        self.w_q = nn.Linear(d_model, d_model, bias=False)  # Wq
        self.w_k = nn.Linear(d_model, d_model, bias=False)  # Wk
        self.w_v = nn.Linear(d_model, d_model, bias=False)  # Wv
        self.w_o = nn.Linear(d_model, d_model, bias=False)  # Wo
        self.dropout = nn.Dropout(dropout)

    @staticmethod
    def attention(query, key, value, mask, dropout: nn.Dropout):
        # 获取d_k的值。
        d_k = query.shape[-1]
        # Q乘以K的转置，除以根号下d_k。
        # (batch, h, seq_len, d_k) --> (batch, h, seq_len, seq_len)
        attention_scores = (query @ key.transpose(-2, -1)) / math.sqrt(d_k)
        if mask is not None:
            # 给mask为0的位置填入一个很大的负值，这样在进行softmax，注意力就为0。
            attention_scores.masked_fill_(mask == 0, -1e9)
        # 进行softmax，归一化。得到注意力权重
        # (batch, h, seq_len, seq_len)
        attention_scores = attention_scores.softmax(dim=-1)
        if dropout is not None:
            attention_scores = dropout(attention_scores)
        # 注意力权重乘以V，得到更新后的embedding。
        # (batch, h, seq_len, seq_len) --> (batch, h, seq_len, d_k)
        return (attention_scores @ value), attention_scores

    def forward(self, q, k, v, mask):
        # 通过3个全连接层，获取Q、K、V矩阵
        query = self.w_q(q)  # (batch, seq_len, d_model) --> (batch, seq_len, d_model)
        key = self.w_k(k)  # (batch, seq_len, d_model) --> (batch, seq_len, d_model)
        value = self.w_v(v)  # (batch, seq_len, d_model) --> (batch, seq_len, d_model)

        # 对多头进行拆分
        # (batch, seq_len, d_model) --> (batch, seq_len, h, d_k) --> (batch, h, seq_len, d_k)
        query = query.view(query.shape[0], query.shape[1], self.h, self.d_k).transpose(1, 2)
        key = key.view(key.shape[0], key.shape[1], self.h, self.d_k).transpose(1, 2)
        value = value.view(value.shape[0], value.shape[1], self.h, self.d_k).transpose(1, 2)

        # 计算注意力
        x, self.attention_scores = MultiHeadAttentionBlock.attention(query, key, value, mask, self.dropout)

        # 多个头合并
        # (batch, h, seq_len, d_k) --> (batch, seq_len, h, d_k) --> (batch, seq_len, d_model)
        x = x.transpose(1, 2).contiguous().view(x.shape[0], -1, self.h * self.d_k)

        # 乘以输出层
        return self.w_o(x)

上边的代码进行了很好的注释，你可以逐行阅读。有几点需要注意：

forward函数传入的q,k,v是尚未经过全连接层的原始向量，在self-attention里，这里的q,k,v都是token的embedding。并且这里的embedding的形状为（batch,seq_len,d_model)。可见Transformer里的tensor将batch size放在第一个维度，因为Transformer里可以同时对所有token进行处理，并不需要按照序列顺序依次处理。而在RNN里将seq_len放在第一个维度，是因为RNN里是按照序列顺序处理数据，seq_len放在第一个维度会方便一些。

Attention计算时，可以传入一个mask矩阵，mask矩阵用0标记了哪些位置不参与注意力计算。比如对于 token就不必参与注意力计算。对于mask标记了0的位置，在注意力logits值计算完成后，给赋值一个很大的负值，这样在进行softmax后，对于这个位置的注意力就为0。相当于不参加注意力计算。