8.10为什么神经网络可以拟合任意函数
理论上只需要一个隐藏层和一个输出层的神经网络就可以拟合任意函数。有什么办法可以直观的理解呢？下边我们就来详细探讨一下。
8.10.1线性函数
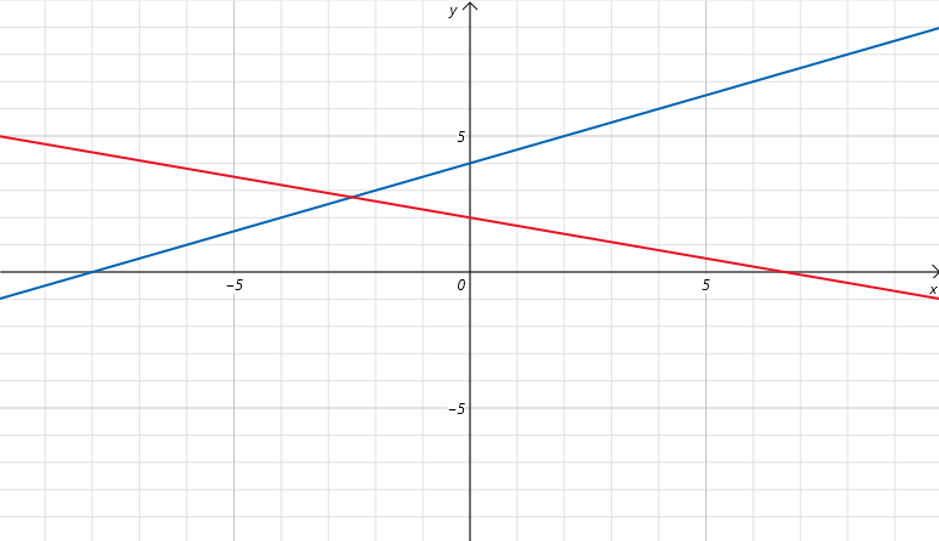我们知道直线方程只用两个参数：斜率和截距，就可以表示二维平面上的任何一条直线。
比如上边图中红色的线为：，蓝色的线为：
线性函数如果不构造高阶特征，只能拟合直线，对于像下边这样的折线就无能为力了：
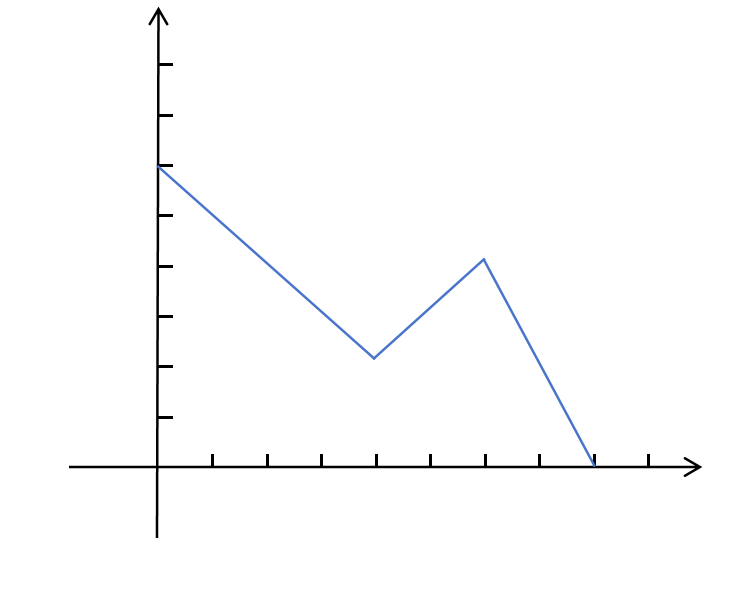
8.10.2分段拟合
很明显上边的折线分为3段，我们可以将它拆成3段分别拟合。
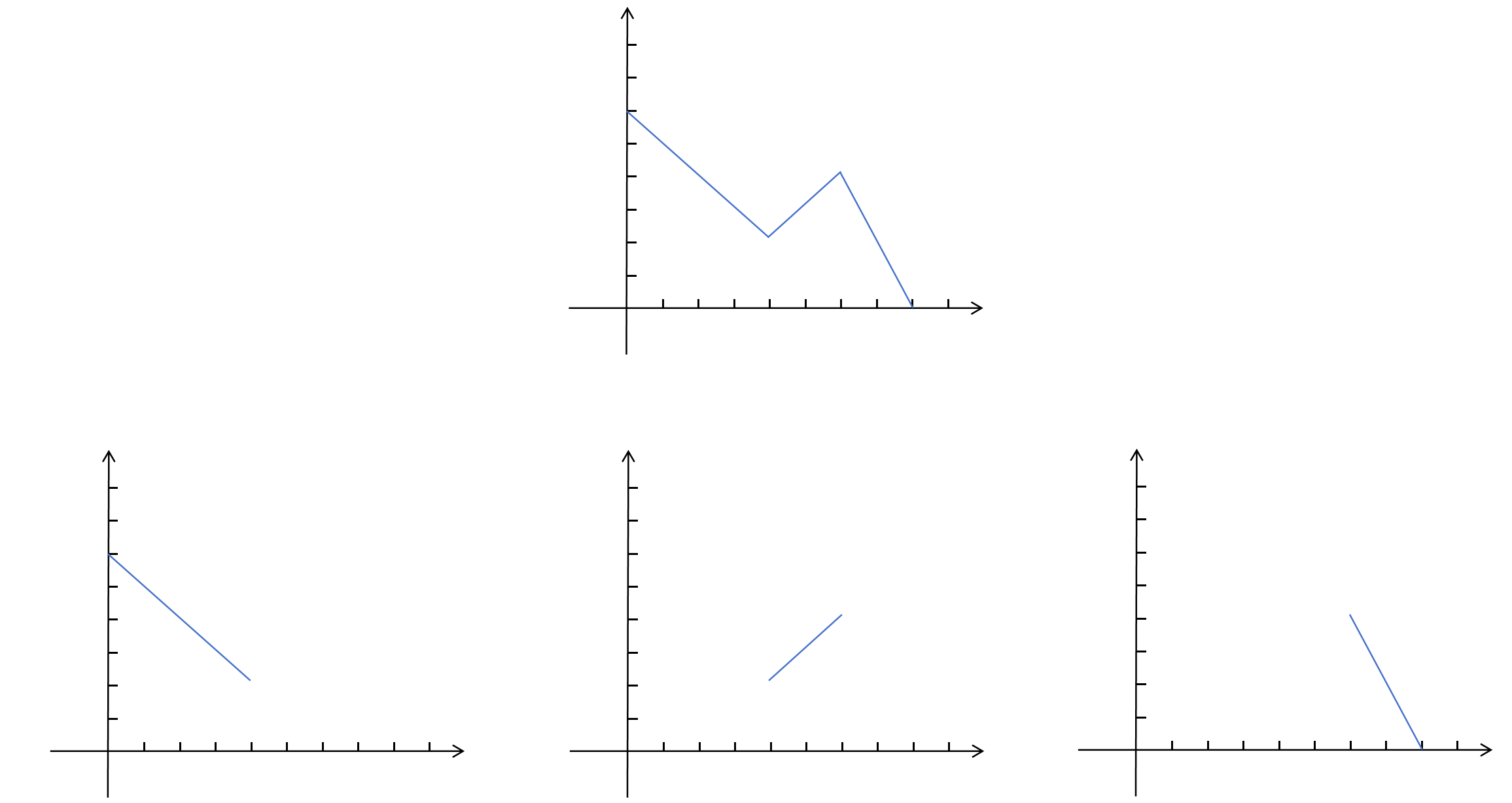
为了让函数在整个值域有定义，我们用直线补齐折线的其他定义域。
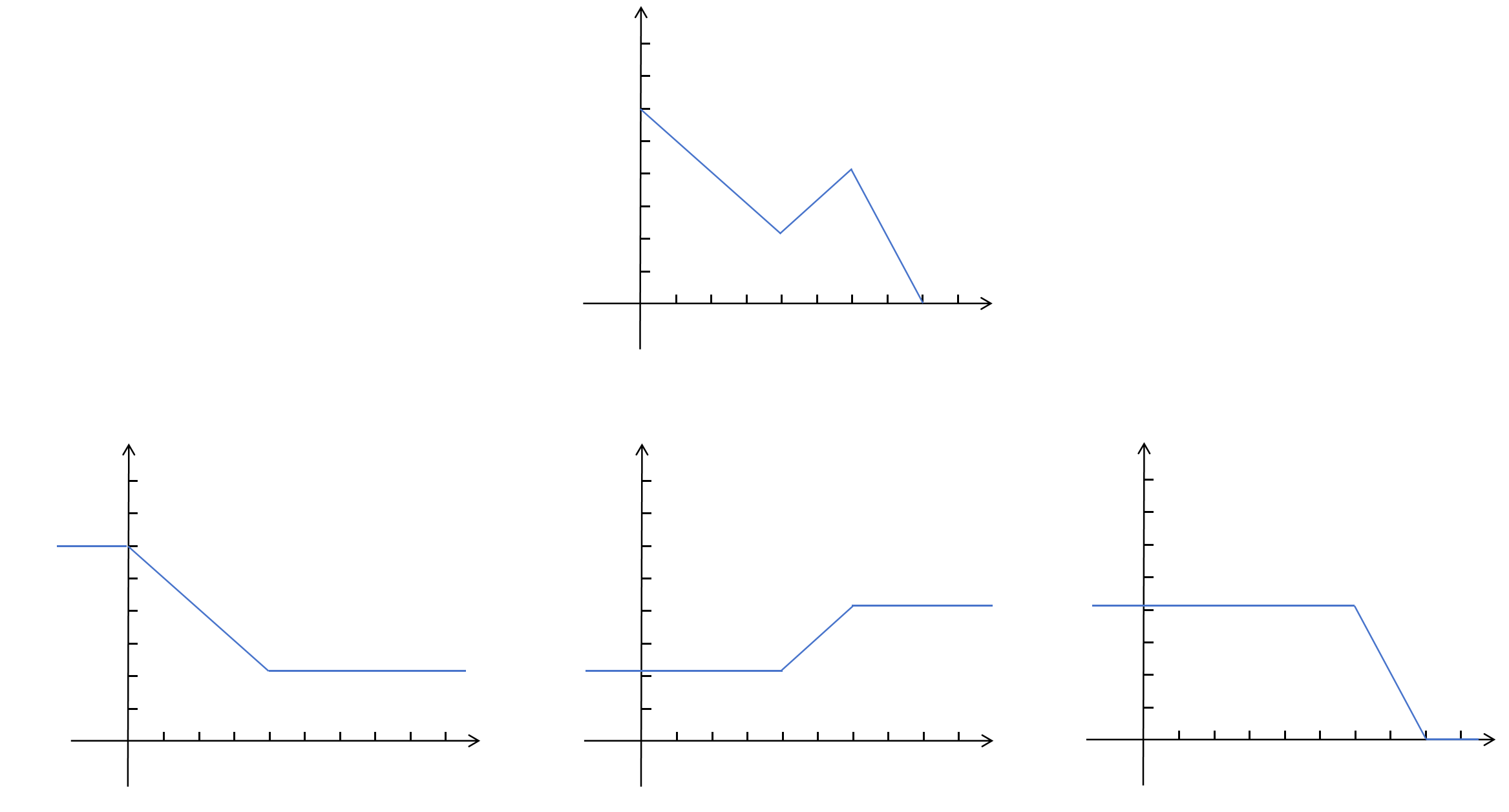
最后做一下调整，除了第一个折线外，让其他折线的起始值都为0。这样就得到下边的三个图像。
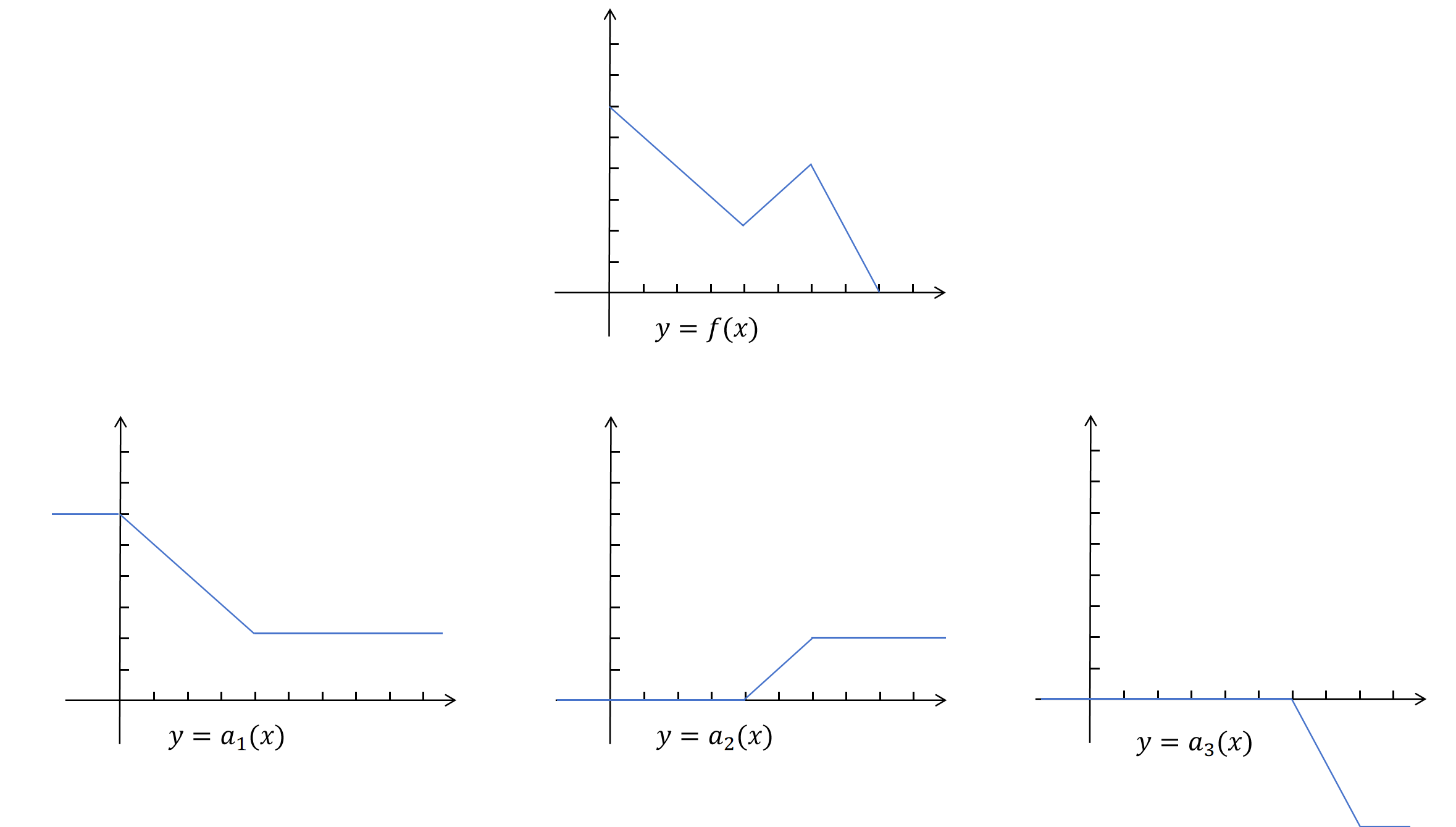
把原始需要我们拟合的函数称为，把下边这三个看起来像阶梯的函数叫做阶梯函数，分别为。经过上边的拆解和平移后，在某一点的取值，就等于在这一点的值。也就是说只要我们能找到拟合阶梯图像的函数，通过把三个阶梯函数加和，我们就可以拟合上边的折线。接下来我们就来寻找合适的阶梯函数。
8.10.3 Sigmoid函数
我们首先来看一下Sigmoid函数的图像：
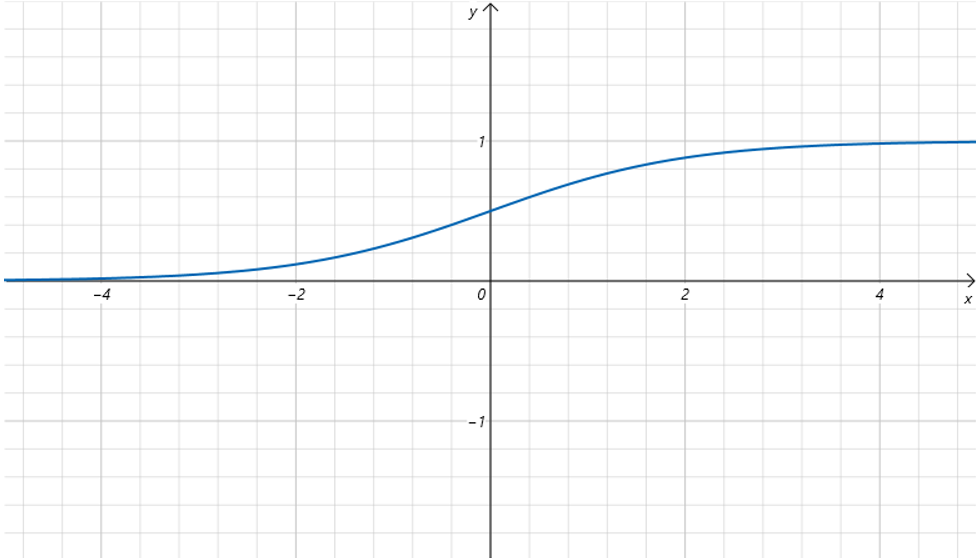
它的函数方程为：
它的图像有一些像阶梯函数。像之前我们通过和可以控制线性函数的图像一样，我们同样给输入x增加上参数和。然后给和设置不同的值，来观察函数图像的变化。修改后的函数方程为：
比如我们设置,图像为：
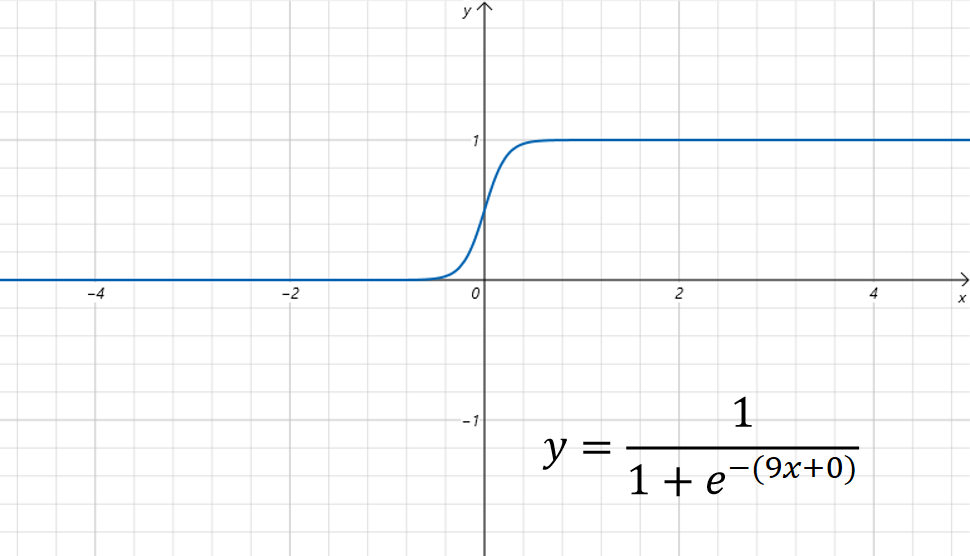它对sigmoid函数沿着x轴方向进行了压缩，看着更像一个阶梯函数了。
接着我们设置,图像为：
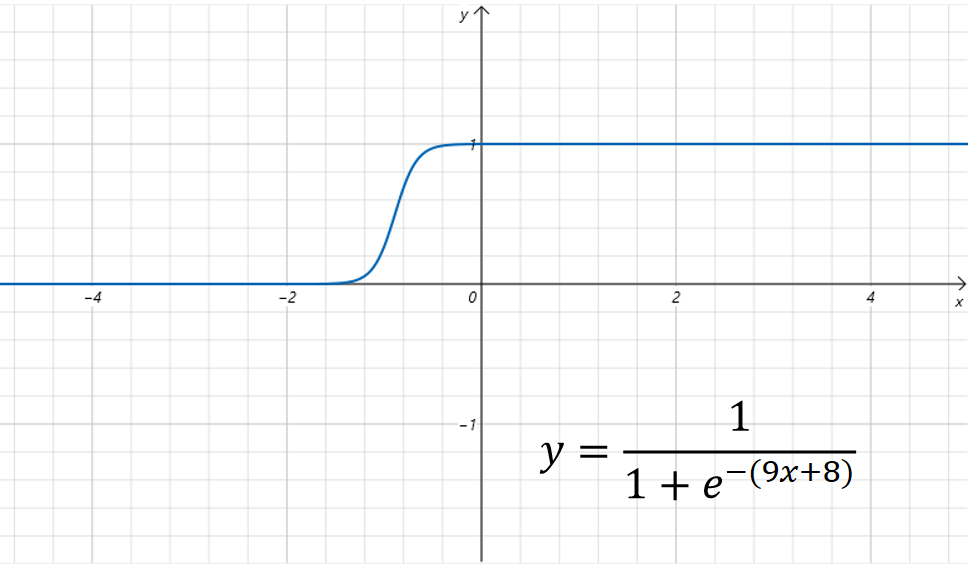可以看到函数图像在之前基础上沿x轴方向进行了平移。
我们设置,图像为：
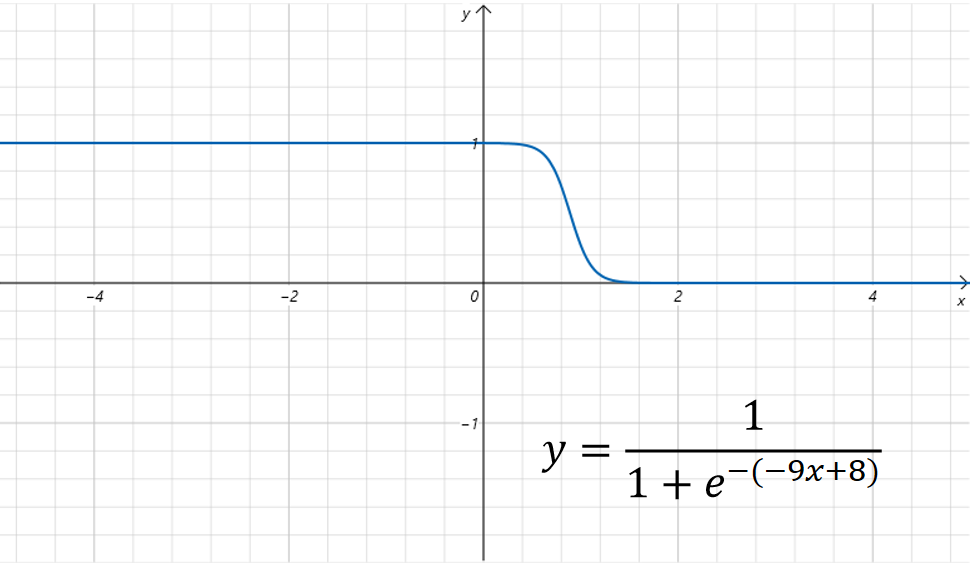
可以看到图像在上一步基础上沿x轴进行了翻转。
经过上边的变化，我们发现通过调整可以让一个Sigmoid的阶梯图像沿着x轴进行平移，翻转，伸缩。但是有一个问题，就是函数的值域一直是0到1，为了调整图像在y轴上的变化，我们对Sigmoid函数的输出也加上两个参数来进行线性控制，这里我们用大写的来表示。
对于上边的例子，我们设置，新的函数图像为：
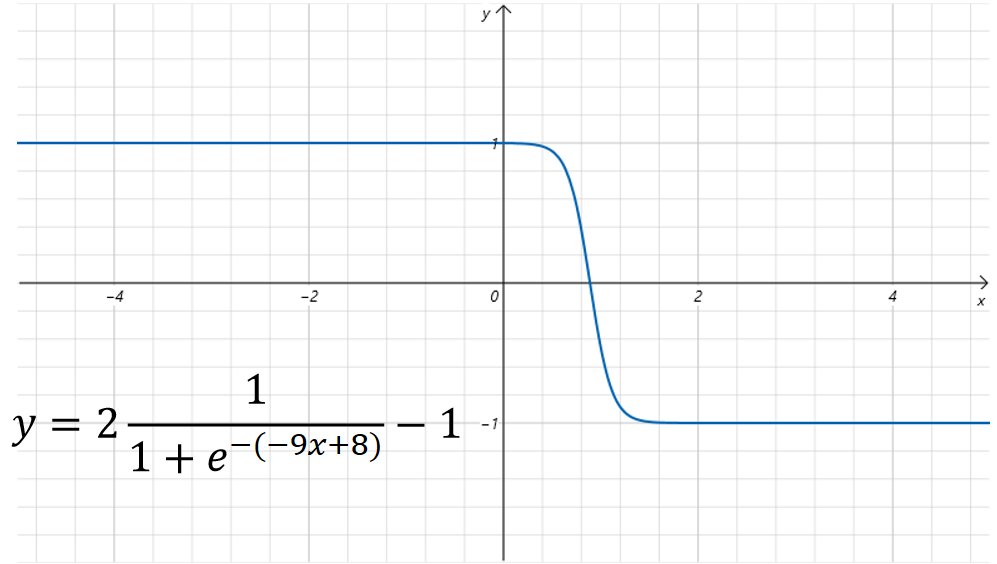
可以看到，它的值域变成了-1到1之间。也就是说，通过增加参数，我们让Sigmoid函数在y轴上也可以拉伸，平移和旋转了。 这样我们就可以得到2维坐标系里任意的一个阶梯函数的拟合图像了。
回到之前我们要拟合的三个阶梯函数，我们通过改造后的Sigmoid函数可以得到类似的图像。如下图所示：
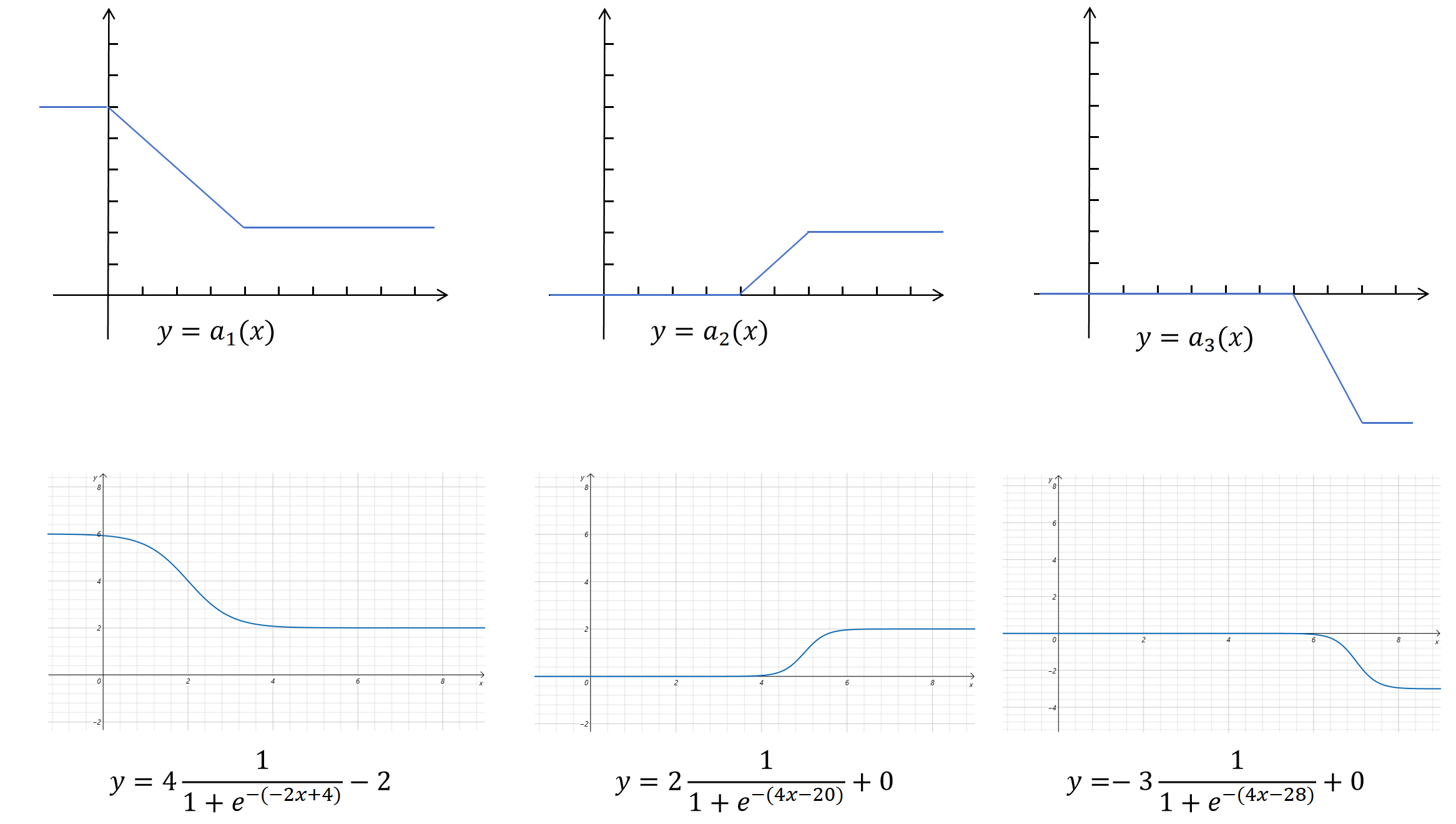
这样我们就可以用这三个Sigmoid拟合的阶梯函数的加和来拟合原始的折线了。
我们是用多个带参数的Sigmoid函数拟合了一个折线，但是这和神经网络有什么关系呢？
实际上3个阶梯函数就代表3个隐藏层的神经元，小写的是隐藏层的权重和偏置。大写的是输出层的权重和偏置。Sigmoid就是每个神经元的激活函数。这个神经网络只有一个输入x，一个输出y。
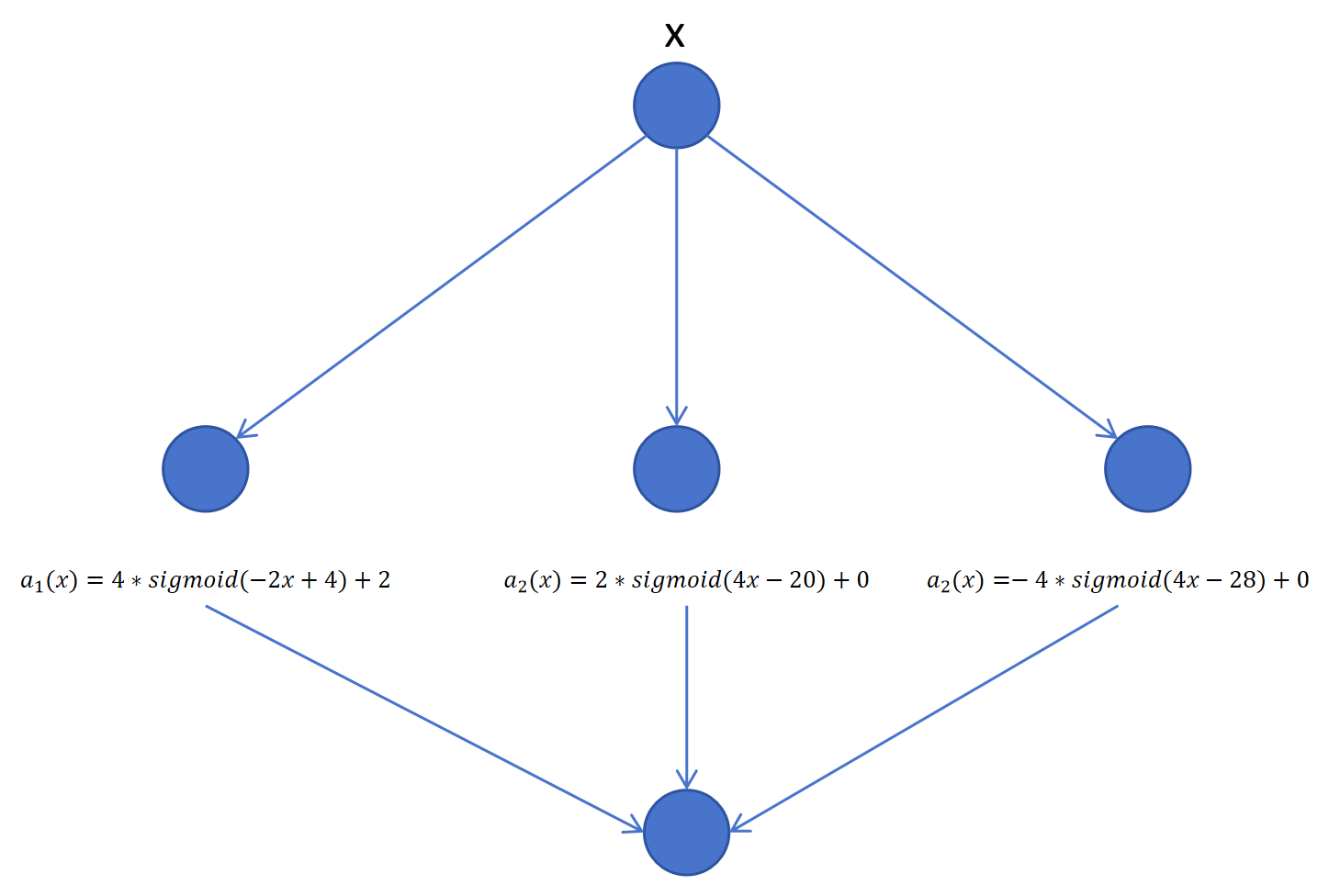
让这些参数都回到它们在神经网络里的位置的话，就如下图：
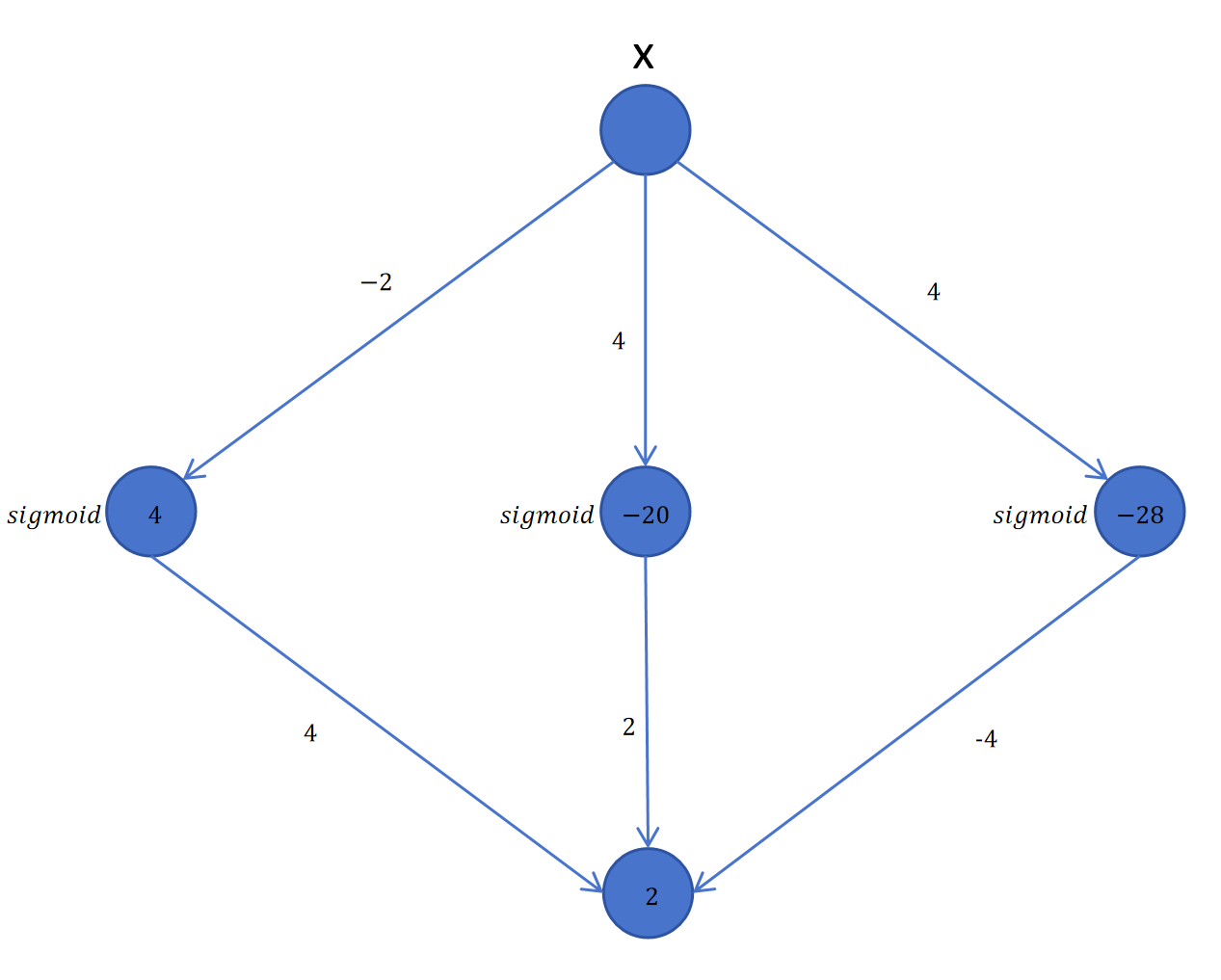
上边我们直观解释了用两层的神经网络来拟合一个3段的折线。任意曲线都可以看做是由很多段的折线拼接构成。所以2层的神经网络理论上可以拟合任意函数。
8.10.4 ReLU函数
你可能会好奇，如果激活函数选择ReLU该怎么拟合呢？Sigmoid函数或者tanh函数本来长得就像阶梯函数，但是ReLU怎么拟合阶梯函数呢？答案是用两个ReLU函数的和来构成一个阶梯函数。
同样我们给ReLU函数也增加四个参数：
这就相当于是一个用ReLU作为激活函数的神经元，我们构造两个这样的神经元。
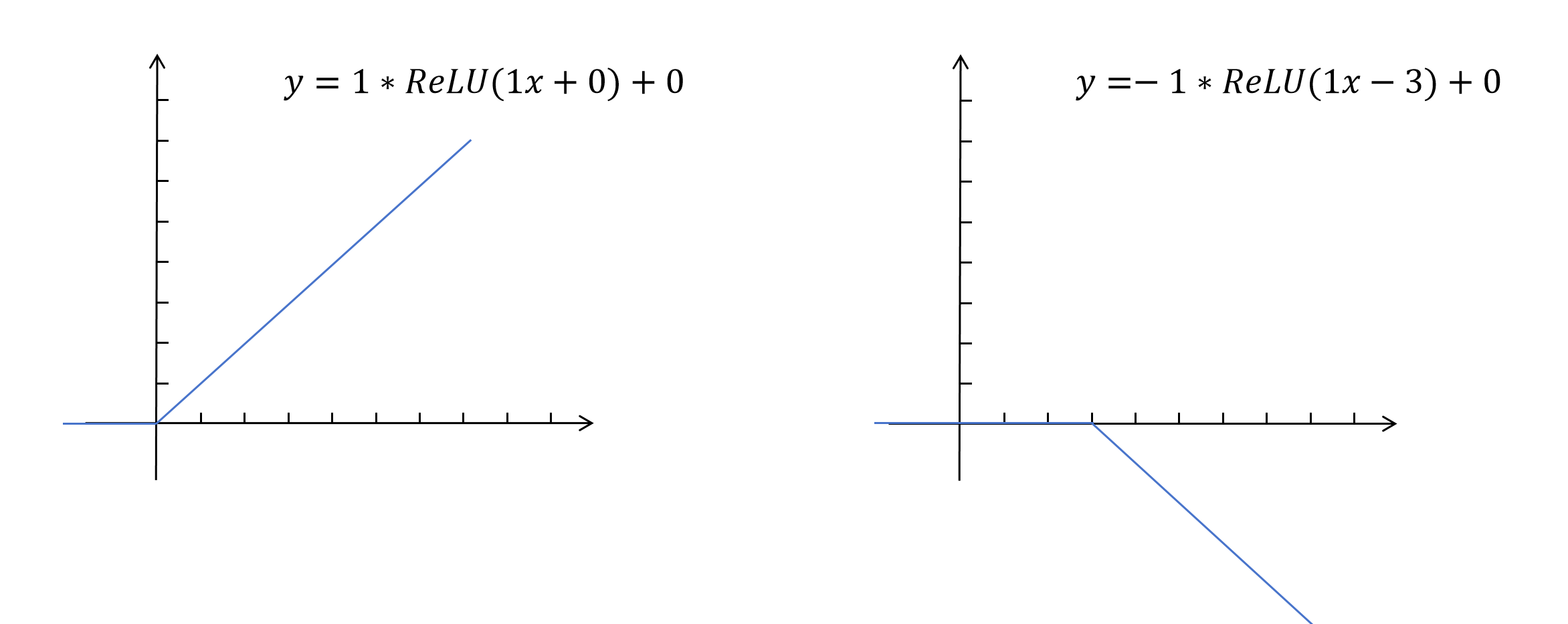
然后，将这两个神经元的输出进行加和，就得到了下边这样的阶梯图像：
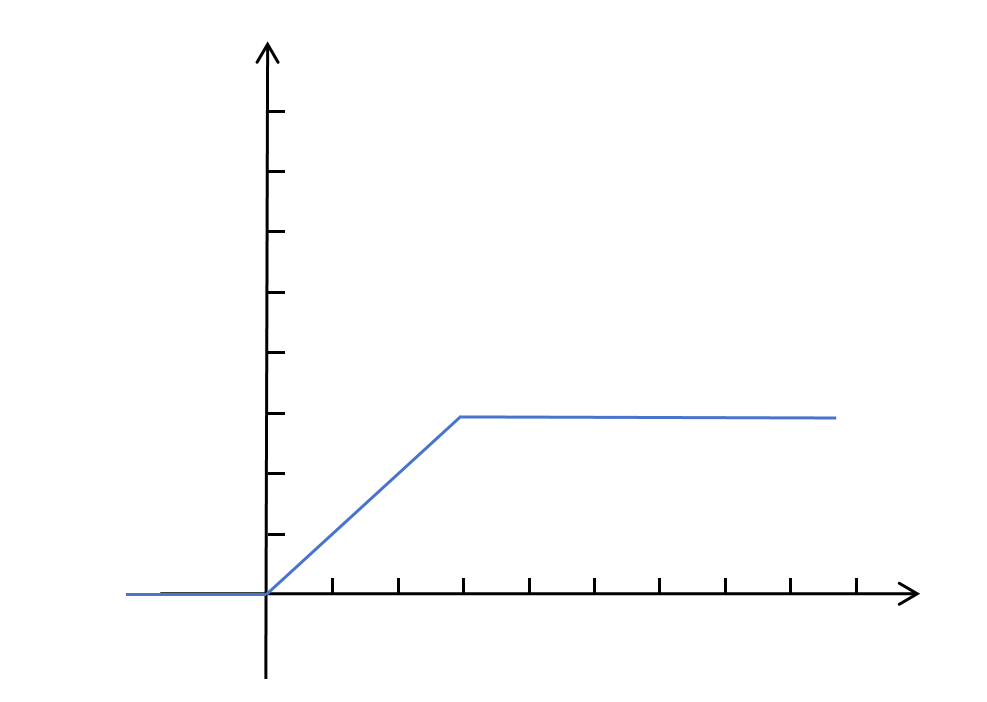
所以用ReLU作为激活函数，也是可以拟合任意函数的。
8.10.5为什么需要深度神经网络
既然两层的神经网络理论上就可以拟合任意函数了，为什么我们还需要深层神经网络？这是因为深层的神经网络可以逐层提取更高级的特征，正是这种逐层抽象的能力大大提升了神经网络的能力。完成同一个任务，两层的神经网络需要的神经元的数量要指数级大于深度神经网络。
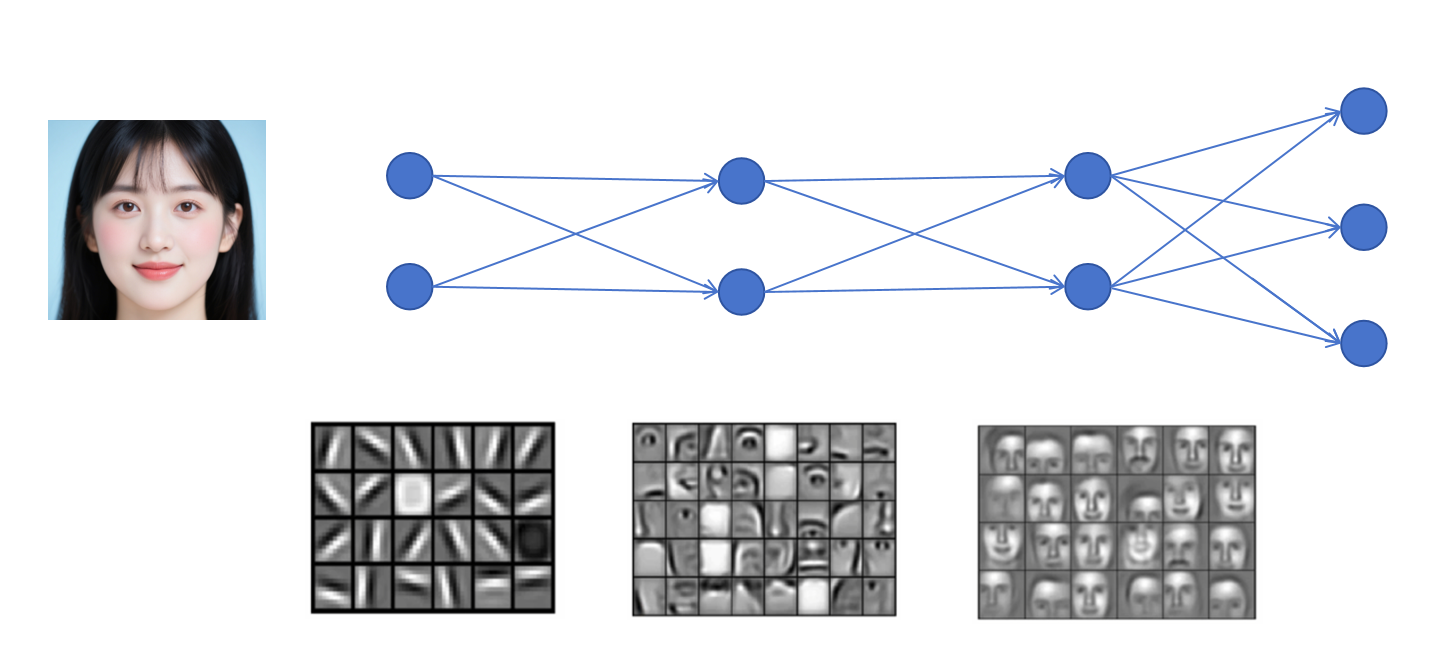就像上边这张图所示，它展示了利用多层神经网络来进行人脸识别。浅层的神经网络提取的是一些简单特征，比如点、线。中间层利用浅层提取的点和线作为输入，识别的是一些脸部器官，比如眼睛，鼻子，嘴巴。而最终深层的网络输入就是眼睛、鼻子、嘴巴这样的器官，最终输出对人脸的识别结果。深度神经网络就是利用了这种逐层抽象的能力来达到好的效果。
逐层抽象，相当于对一个复杂任务做了分解，每一层都在上一层的基础上进行简单的组合和加工。每一层要学习的内容就简单。模型更容易达到好的效果。有研究论文发现，同等参数量的模型，一个浅而宽的神经网络效果是远不如一个窄而深的神经网络的。当然每一层的神经元也不能太少，至少要能学习到这一层的所有模式才行，这一层是学习的人脸的器官，那必须有神经元分别是识别眼睛、眼镜、眉毛、额头、嘴巴、鼻子、耳朵、脸颊、下巴等等。