11.9 语义分割

目标检测可以给出图片上目标的边界框。但是在某些情况下这个精度还不够，比如你想从照片中，识别出人像，并且把背景进行虚化。这时候你就需要知道图片中每个像素是人像还是背景。再比如对于卫星遥感照片，需要识别地面上森林的面积，森林的形状是不规则的。这时，就需要能识别遥感照片上每个像素是否属于森林。

这种需要对图片上每个像素都赋予语义信息的任务叫做语义分割（semantic segmentation）。

这一节我们就来了解一下语义分割的基本原理。

11.9.1 语义分割的原理

语义分割任务实际上就是对原始图片上的每一个像素进行多分类。比如我们要对原始图片进行语义分割，其中类别包括：背景，行人，汽车，摩托车。输入的图片特征为224×224×3，那么经过语义分割的神经网络后，输出的特征图高宽应该一样，但是通道数为4，对应要分类的4个类别。所以最终输出的特征图形状为224×224×4。每个像素上都有4个特征，对这4个特征应用softmax，进行4分类，最终给出每个像素的分类值。

主流的语义分割网络都是先利用卷积神经网络对图片进行下采样，得到高级语义特征。然后利用转置卷积将特征图上采样到原始图片大小，再对图像每个像素进行分类。

11.9.2 转置卷积

我们之前讲过的卷积操作，如果不加Padding，卷积核不为1×1，那么经过卷积操作，特征图的高和宽总是会变小。而转置卷积是一种特殊的卷积操作，它可以放大特征图的高和宽。

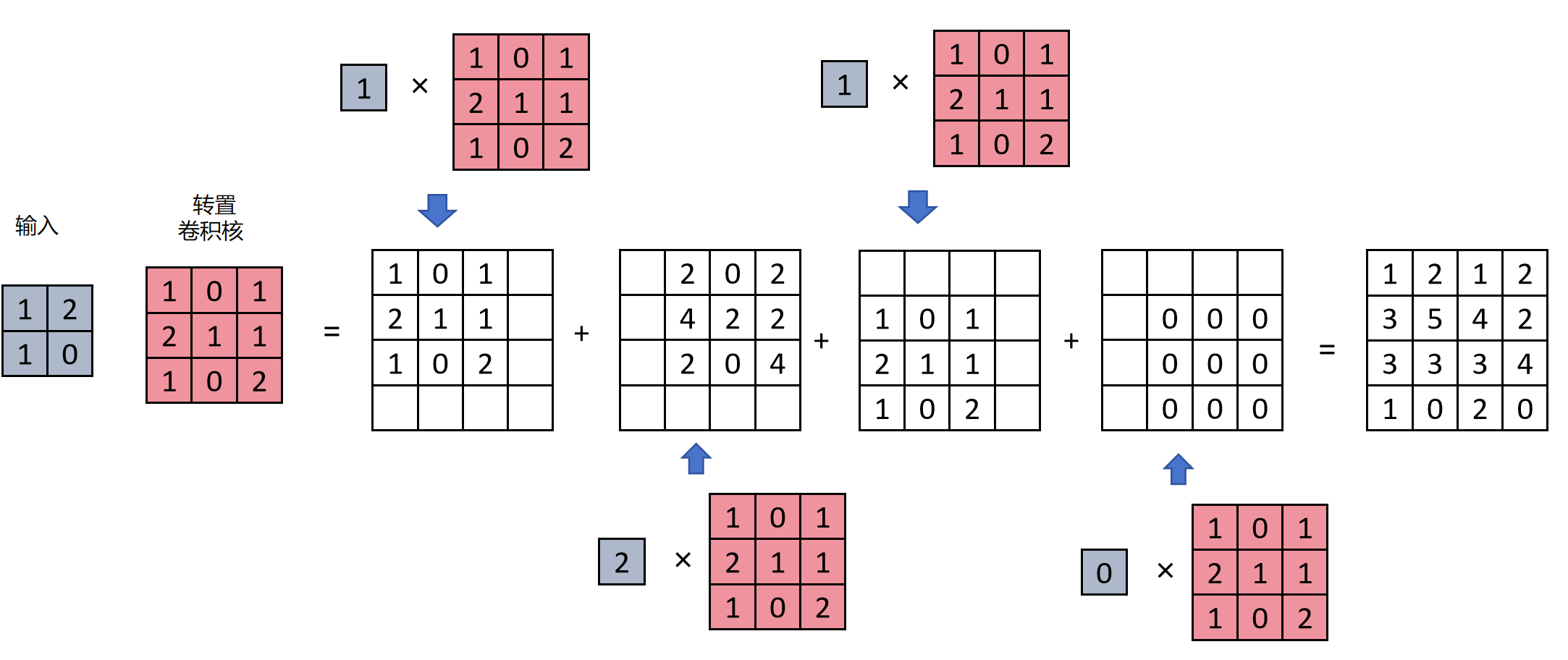
上图是一个转置卷积的计算过程。输入是2×2的特征图，转置卷积核的形状为3×3。进行转置计算时，步长为1。

• 第一步，取出输入特征中左上角第一个元素：1，与卷积核相乘，得到一个矩阵。
• 第二步，取出输入特征中右上角第二个元素：2，与卷积核相乘，因为步长为1，右移一位。
• 第三步，取出输入特征中左下角第三个元素：1，与卷积核相乘，因为步长为1，下移一位。
• 第四步，取出输入特征中右下角第四个元素：0，与卷积核相乘，因为步长为1，右移一位。
• 第五步，将上边四步的矩阵相加，最终得到一个4×4的扩充的特征图。

如果步长为2，则计算过程如下图：

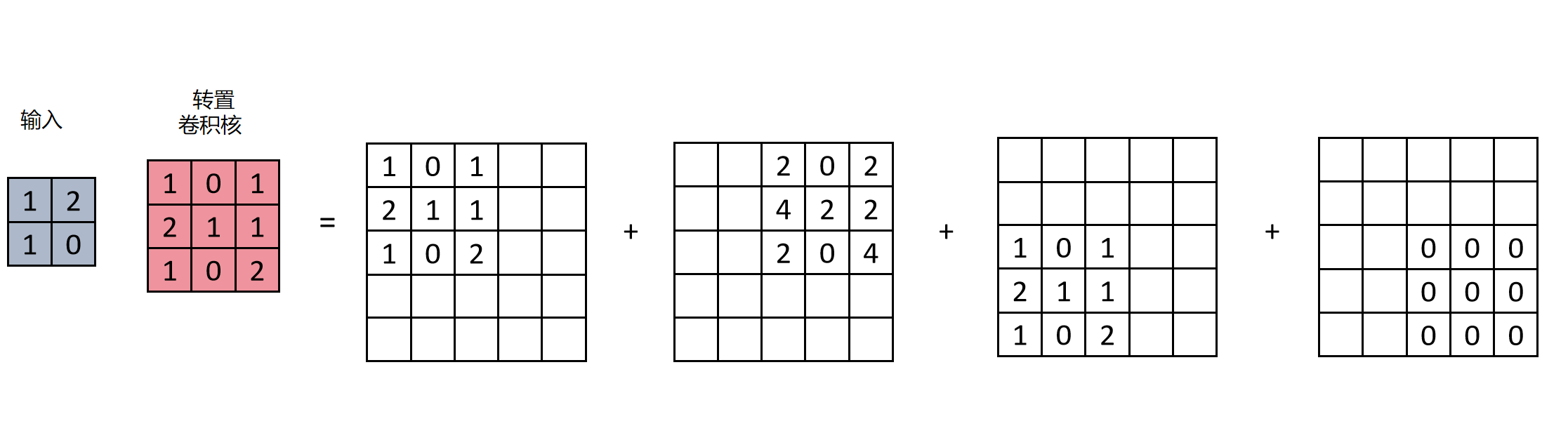
同样，转置卷积的卷积核参数是在训练过程中学到的。通过学习，它知道如何上采样能保持图像的语义信息。

11.9.3 U-Net原理

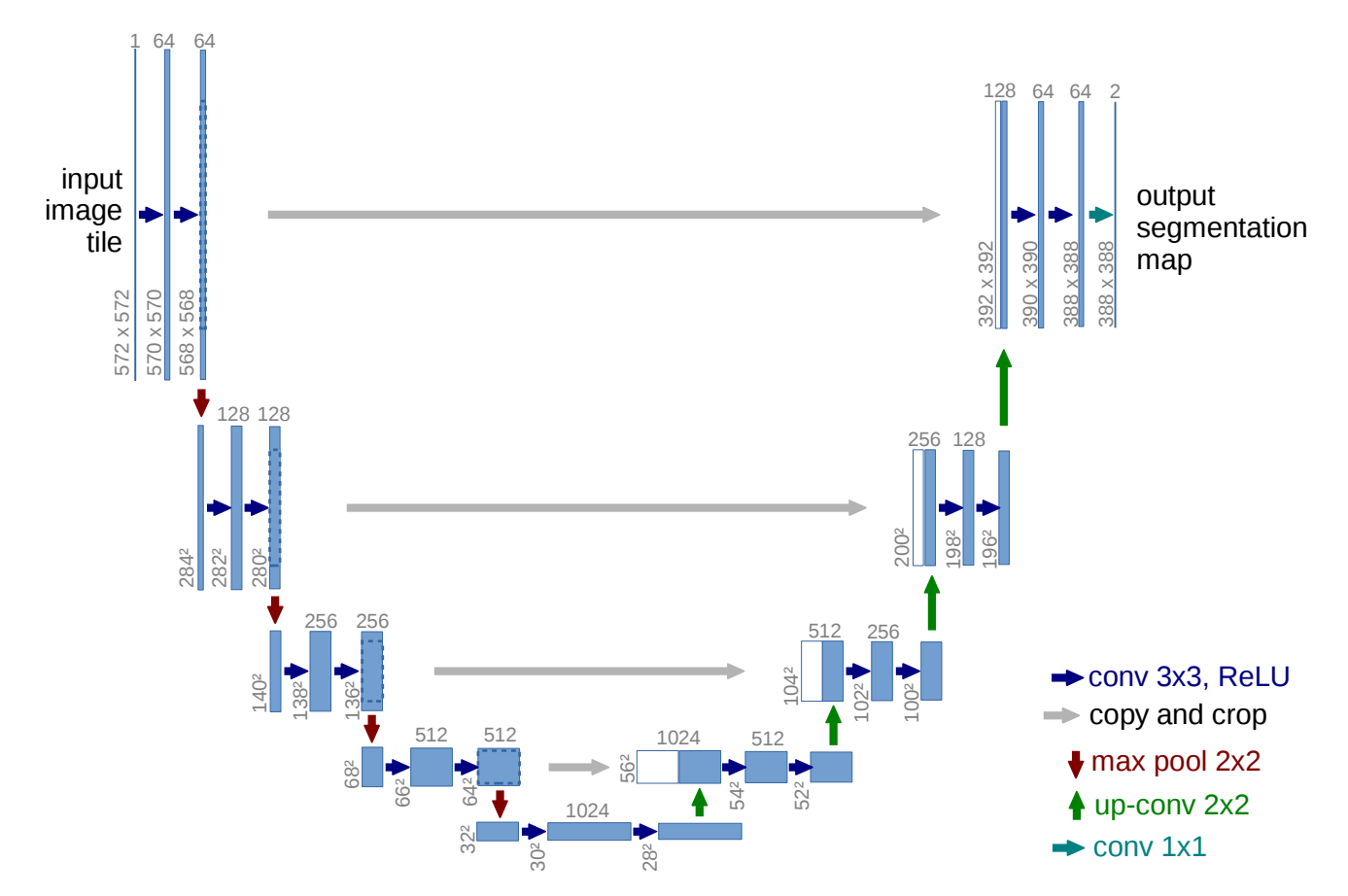U-Net的网络结构图如上图所示，因为其像字母U，而命名为U-Net。 U-Net 的网络主要分为两个部分： 编码器（Encoder）——下采样路径 解码器（Decoder）——上采样路径 此外还有一条贯穿左右的 跳跃连接（Skip Connections），它是 U-Net 的核心创新之一。 编码器（收缩路径） 编码器类似于传统的卷积神经网络，用于提取图像的特征。它通常由若干个卷积层和最大池化层组成。每一次下采样操作都会减小特征图的空间分辨率，但增加通道数，从而捕捉到更深层次的语义信息。 解码器（扩展路径） 解码器通过上采样操作逐步恢复图像的空间分辨率。每一步中都包括上采样（如反卷积或上采样插值）和卷积操作。其目的是根据高层特征图还原出原图大小的分割结果。 跳跃连接（Skip Connections） U-Net 的一个关键特点是，它在每个上采样步骤中，把编码器中对应层的特征图与解码器当前的特征图进行拼接（concatenate）。这样可以保留低层的空间信息，使得模型在恢复图像时更加精细。这种跳跃连接机制帮助 U-Net 解决了图像细节信息在下采样过程中丢失的问题。让网络既能“看的懂”，又能“看的清”。 U-Net 的输出 最后一层使用一个 1×1 的卷积操作，将多通道特征图映射为类别数通道。然后使用 softmax 函数进行像素级别的分类。

需要注意的是U-Net原始论文里进行跳跃连接时，两边特征图的高宽并不一致，需要进行裁剪，这样很麻烦。两边特征图高宽的不一致是因为原论文3×3卷积并没有加Padding，导致特征图尺寸的变化。后来为了方便，实现时大家都利用加Padding的卷积层，保证了跳跃连接时两边特征图高宽的一致。

11.9.4 U-Net实现

import torch
import torch.nn as nn

class DoubleConv(nn.Module):
    """两个连续的 3x3 Conv（padding=1）+ BN + ReLU"""
    def __init__(self, in_ch, out_ch):
        super().__init__()
        self.double_conv = nn.Sequential(
            nn.Conv2d(in_ch, out_ch, kernel_size=3, padding=1, bias=False),
            nn.BatchNorm2d(out_ch),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_ch, out_ch, kernel_size=3, padding=1, bias=False),
            nn.BatchNorm2d(out_ch),
            nn.ReLU(inplace=True),
        )
    def forward(self, x):
        return self.double_conv(x)

class UNet(nn.Module):
    def __init__(self, in_ch, out_ch):
        super().__init__()
        # 编码路径
        self.conv1 = DoubleConv(in_ch, 64)
        self.pool1 = nn.MaxPool2d(kernel_size=2)
        self.conv2 = DoubleConv(64, 128)
        self.pool2 = nn.MaxPool2d(kernel_size=2)
        self.conv3 = DoubleConv(128, 256)
        self.pool3 = nn.MaxPool2d(kernel_size=2)
        self.conv4 = DoubleConv(256, 512)
        self.pool4 = nn.MaxPool2d(kernel_size=2)
        self.conv5 = DoubleConv(512, 1024)  # 最底层

        # 解码路径
        self.up6 = nn.ConvTranspose2d(1024, 512, kernel_size=2, stride=2)  # 上采样 ×2
        self.conv6 = DoubleConv(1024, 512)  # 拼接后通道数变为 512+512=1024

        self.up7 = nn.ConvTranspose2d(512, 256, kernel_size=2, stride=2)
        self.conv7 = DoubleConv(512, 256)

        self.up8 = nn.ConvTranspose2d(256, 128, kernel_size=2, stride=2)
        self.conv8 = DoubleConv(256, 128)

        self.up9 = nn.ConvTranspose2d(128, 64, kernel_size=2, stride=2)
        self.conv9 = DoubleConv(128, 64)

        self.final_conv = nn.Conv2d(64, out_ch, kernel_size=1)

    def forward(self, x):
        # 编码
        c1 = self.conv1(x)      # c1: [B, 64, H, W]
        p1 = self.pool1(c1)     # p1: [B, 64, H/2, W/2]
        c2 = self.conv2(p1)     # c2: [B,128, H/2,W/2]
        p2 = self.pool2(c2)     # p2: [B,128, H/4,W/4]
        c3 = self.conv3(p2)     # c3: [B,256, H/4,W/4]
        p3 = self.pool3(c3)     # p3: [B,256, H/8,W/8]
        c4 = self.conv4(p3)     # c4: [B,512, H/8,W/8]
        p4 = self.pool4(c4)     # p4: [B,512, H/16,W/16]
        c5 = self.conv5(p4)     # c5: [B,1024,H/16,W/16]

        # 解码，第 1 级上采样
        u6 = self.up6(c5)       # u6: [B,512, H/8,W/8]
        # 直接拼接 c4（[B,512,H/8,W/8]）和 u6
        u6 = torch.cat([c4, u6], dim=1)  # 拼接后：[B,1024,H/8,W/8]
        c6 = self.conv6(u6)     # c6: [B,512, H/8,W/8]

        # 解码，第 2 级
        u7 = self.up7(c6)       # u7: [B,256, H/4,W/4]
        u7 = torch.cat([c3, u7], dim=1)  # [B,512, H/4,W/4]
        c7 = self.conv7(u7)     # [B,256, H/4,W/4]

        # 解码，第 3 级
        u8 = self.up8(c7)       # [B,128, H/2,W/2]
        u8 = torch.cat([c2, u8], dim=1)  # [B,256, H/2,W/2]
        c8 = self.conv8(u8)     # [B,128, H/2,W/2]

        # 解码，第 4 级
        u9 = self.up9(c8)       # [B,64, H, W]
        u9 = torch.cat([c1, u9], dim=1)  # [B,128,H,W]
        c9 = self.conv9(u9)     # [B,64, H, W]

        # 最后一层 1x1 卷积，得到最终预测
        out = self.final_conv(c9)  # [B,out_ch,H,W]
        return out