5.6 线性回归只能拟合直线吗

很多学完线性回归的人都觉得线性回归太过于简单，以至于没有什么使用价值，因为显示生活中Label和Feature之间很多并不满足线性关系。

5.6.1一个非线性的例子

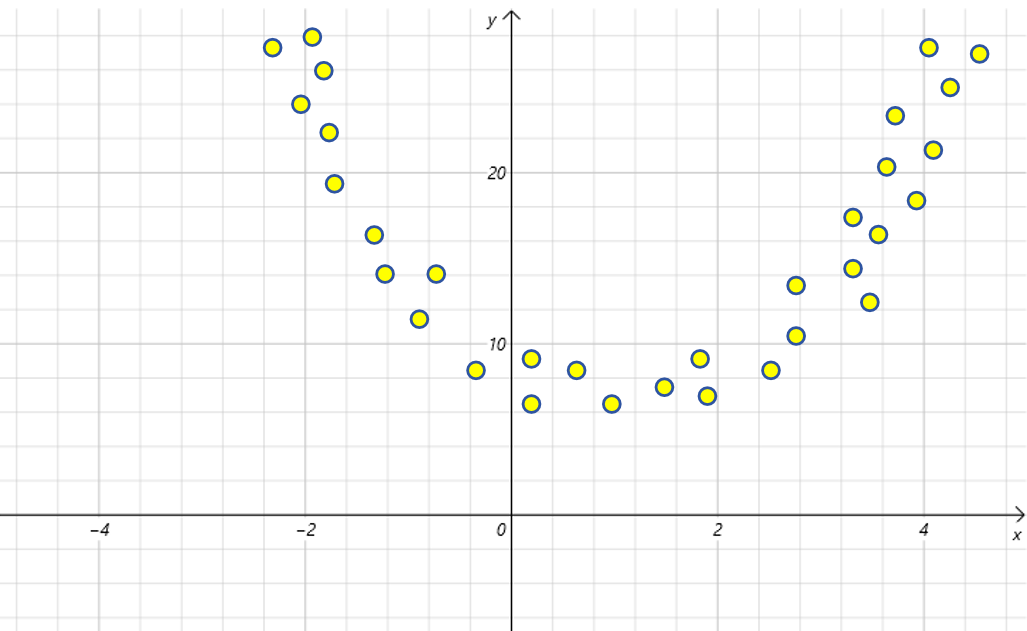
如果把上图看做feature是x，label是y，那么确实不能用一个直线来拟合x和y之间的关系。通过观察图像，我们知道这个图像符合一元二次函数的图像。也就是说要拟合这个曲线，我们的假设函数应该是如下形式：

5.6.2构造新的特征

原始的训练样本里只有feature $x_1$，label y。并且x是已知的值，我们可以构造一个新的特征$x_2=x_1^2$。 那么我们的假设函数就变成了：

可以看到假设函数又变成了线性表达式。其中$w_0,w_1,w_2$是我们要优化的参数。$x_1,x_2$是特征，只不过$x_2=x_1^2$。

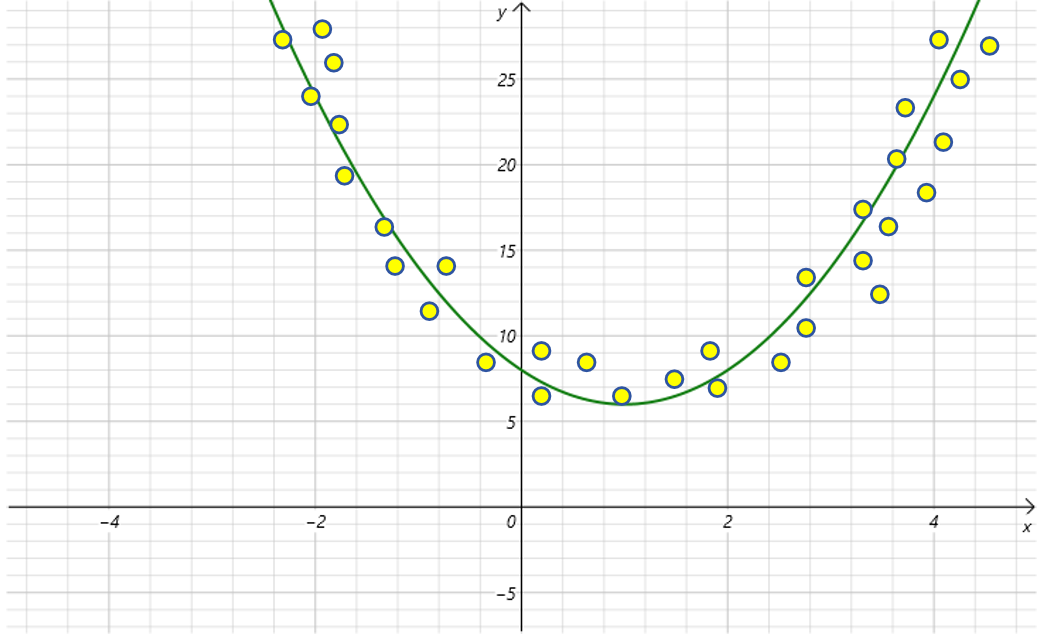
通过优化，我们可以得到$w_0,w_1,w_2$的值：

5.6.3更一般的推广

上边我们是通过观察图像，认为假设函数里应该有x的二次项。然后通过构造$x^2$这个新的特征，最后用线性回归来拟合每个特征的权重的。那对于其他不规则的曲线呢？我们该怎么构造特征呢？

泰勒公式告诉我们，任何一个光滑的、n阶可导的函数，在某一点附近都可以用一个多项式函数来近似。这意味着，即使我们面对的函数关系非常复杂，只要我们选择足够高的多项式次数，就可以用线性回归模型在局部范围内很好地拟合它。

下边我们看个例子，比如对于y=sin(x)的曲线，也可以通过构造x的高次项，转化为一个线性问题。

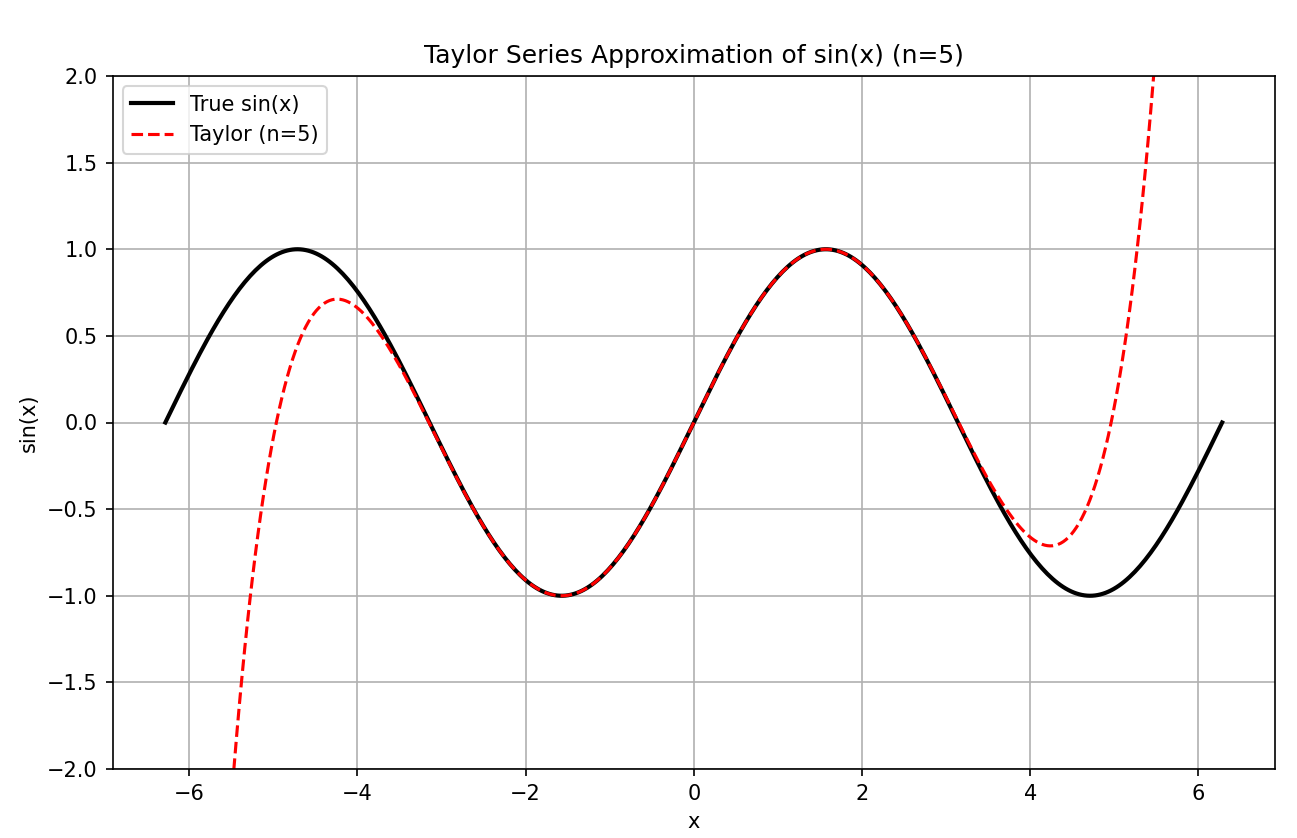
上图中黑色的曲线是sin(x)。 红色的项是通过泰勒公式展开的x的多项式：

当然如果你添加更多的x的高次项，会拟合的更好。

如果模型有多个特征，还可以构造出多个特征之间相乘的高次项。比如你要预测房价，你收集的feature里有房子的长度，有房子的宽度。那么你可以构造一个新的feature，它的值等于长度乘以宽度。也就是房子的面积。

通过本节的学习，我们知道对于特征和Label之间的非线性问题，我们可以通过构造高次特征来解决。一般的做法是先从二次项开始，逐步增加，直到达到我们满意的效果。假如你在构造特征的二次项，需要注意的是，构造的特征不光可以是一个特征的平方，也可以是任意两个特征之间的乘积。