7.1一元逻辑回归

之前我们研究了回归问题，也就是根据一个或者多个特征，预测一个连续的目标。比如预测温度，预测房价，预测销量等，这都是回归问题。实际应用中，还有另一类应用非常广的算法就是分类算法，比如根据用户的特征判断用户会不会违约。根据一朵花花瓣和花萼的长度宽度，预测花的种类等。根据用户特征，判断用户会不会点击这个广告。

这一节我们学习一个分类问题的算法。千万不要被逻辑回归里的“回归”误导，逻辑回归是一个分类问题的算法。这也是机器学习历史遗留的用词不规范的地方。

7.1.1气温与是否出门

我们从一个例子开始，假设你统计了小明每天是否出门与当天气温的数据。0代表不出门，1代表出门。

气温	是否出门
-10	0
3	1
-3	0
5	1
-4	0
7	1
-6	0
8	1

将上边的数据绘制散点图如下：

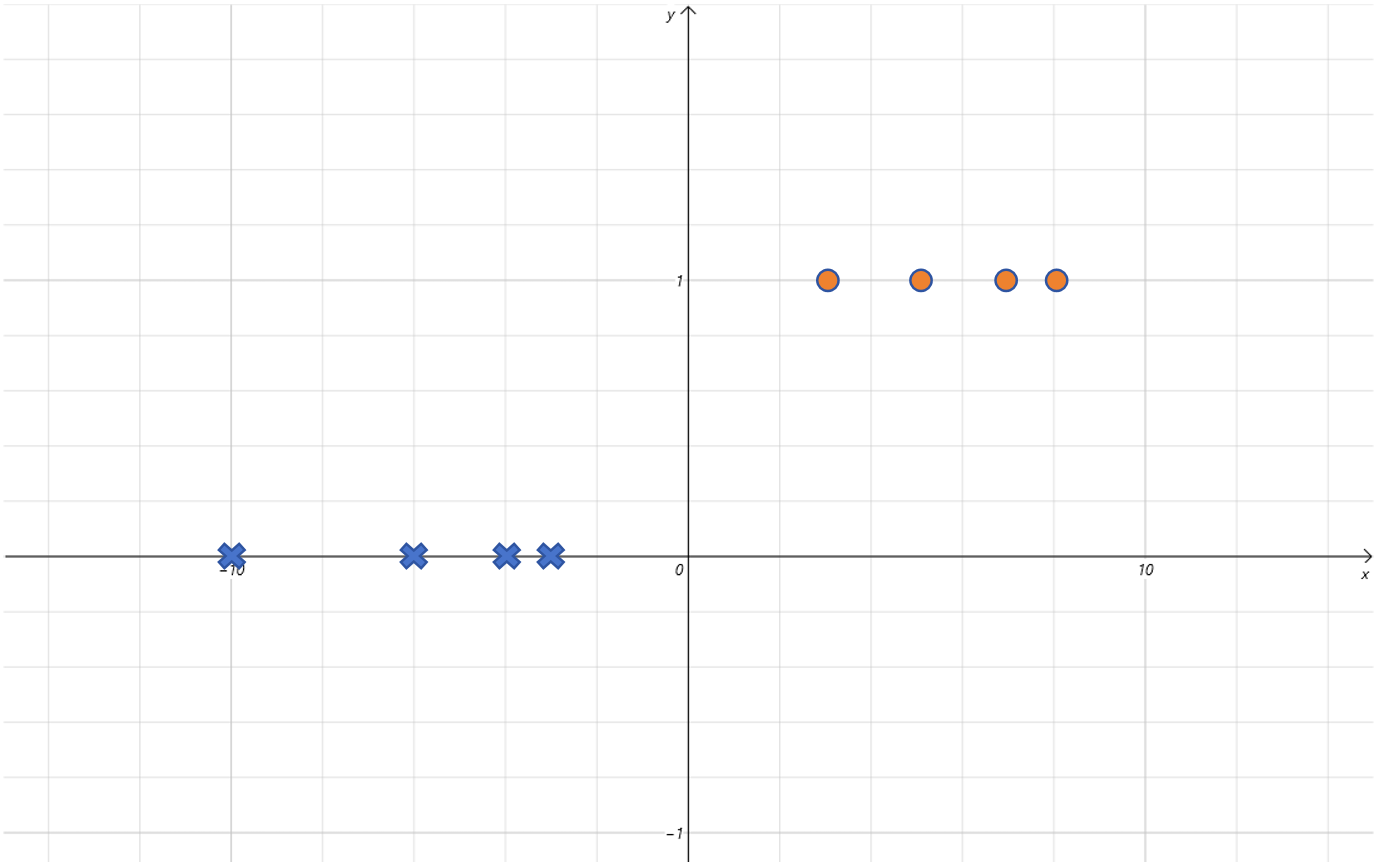
我们需要训练一个模型，根据气温来预测小明是否出门。回想我们之前学过的线性回归模型，感觉用在这里不合适。因为这里Label的取值只有两个，非0即1，是个分类问题。如果用简单的一元一次线性方程，它预测的Label会一直变化，突破[0,1]的范围，所以是不能拟合这个图像的。

既然线性函数不适合，那人们就寻找其他函数。最后找到这么一个函数，Sigmoid函数：

sigmoid(x)=\frac{1}{1+e^{-x}}

将这个函数的曲线绘制出来，如下：

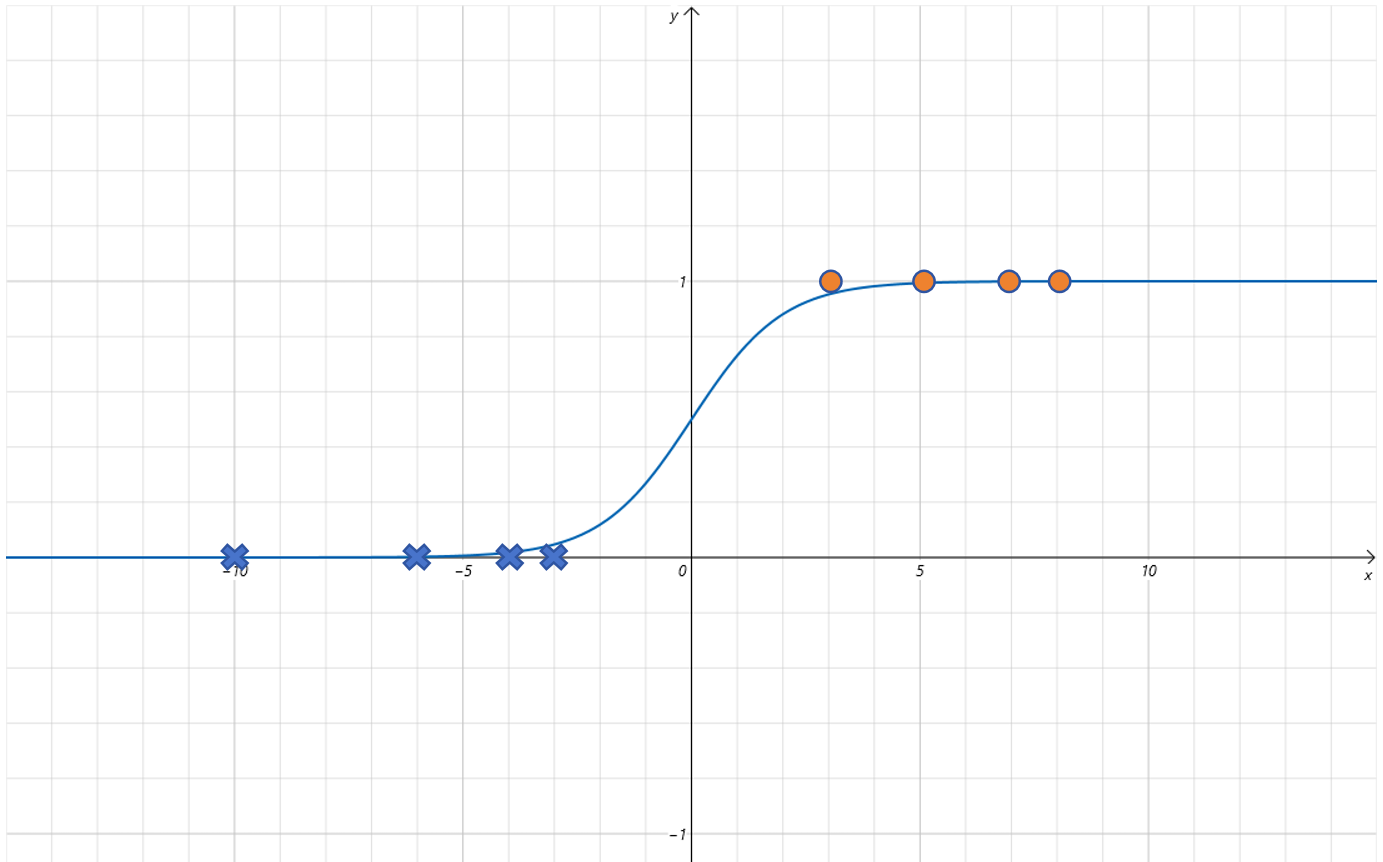
可以看到Sigmoid函数有很好的特性，它的输出值区间为[0,1]，而且只有x取值在0附近时，函数值有明显的变化，其他区间都很非常接近0或者1。

我们可以把Sigmoid的函数值作为在气温为x下，对小明出门概率的预测。比如当气温为-10时，预测小明出门的概率接近0，气温为10，预测小明出门的概率接近1。在气温为-1时，预测小明出门概率大概为0.3，气温为0是，预测出门概率为0.5。

所以，用Sigmoid函数可以很好的作为二分类问题的假设函数。线性回归的假设函数为线性方程，它假设Feature和Label之间满足线性关系。而二分类问题的假设函数就为Sigmoid，它假设输入x和输出y之间满足Sigmoid函数的映射关系。

7.1.2给Sigmoid函数增加缩放参数

等等，好像有什么不对的地方。用Sigmoid函数作为假设函数，里边完全没有可以训练的参数。Sigmoid函数的图像完全是固定的，但是不是所有的二分类问题都可以映射到标准的Sigmoid函数上。

实际上，即使对上边的例子，直接利用Sigmoid函数拟合的也不是很好。比如对于温度为3和-3时。我们可以给Sigmoid函数里的x前边增加一个参数w。

sigmoid(wx)=\frac{1}{1+e^{-wx}}

我们试着调整w这个参数。

当设置w为0.5时：

sigmoid(0.5x)=\frac{1}{1+e^{-0.5x}}

函数曲线变为：

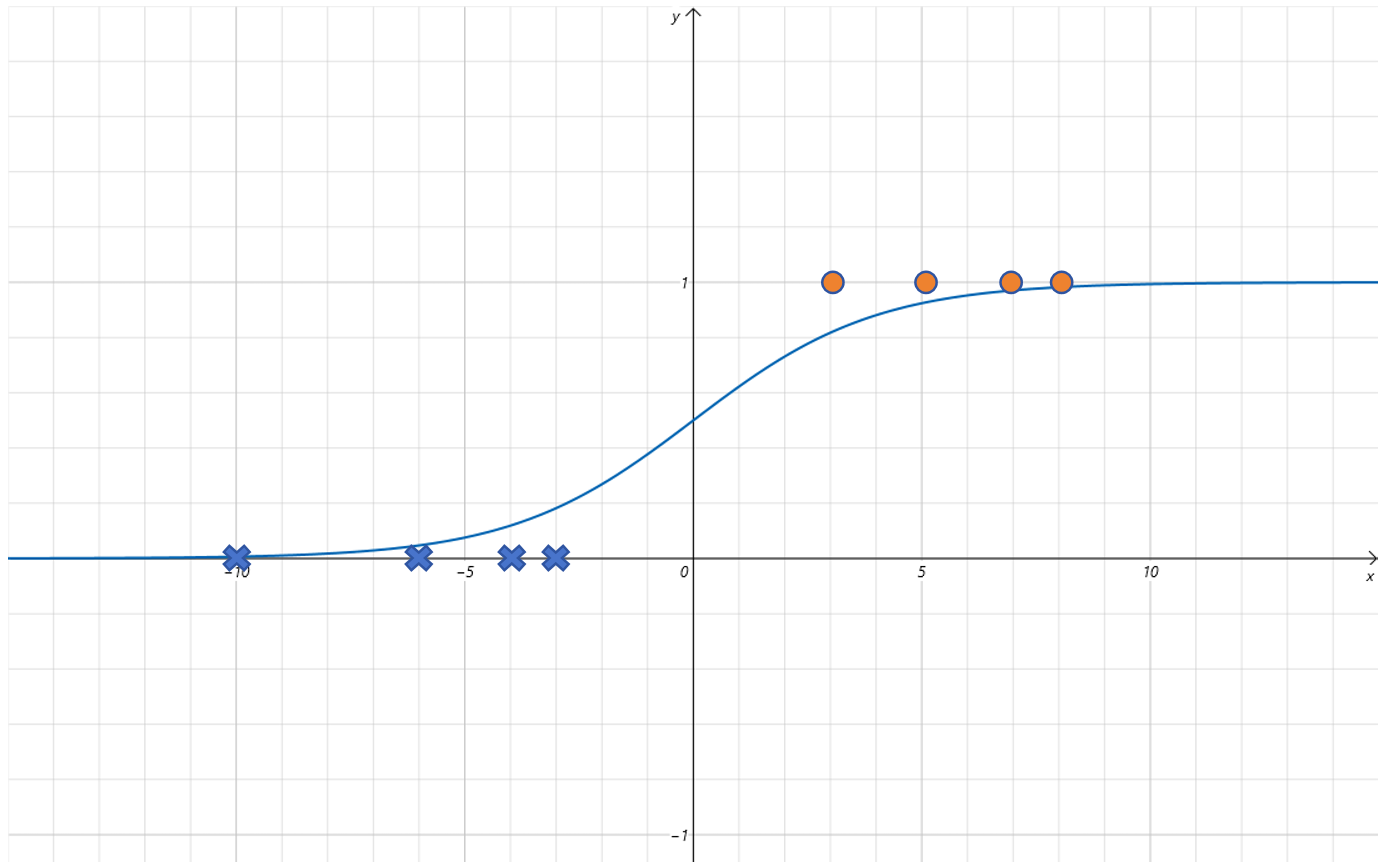
可以发现函数曲线沿着x轴方向拉伸了。

当设置w为2时：

sigmoid(2x)=\frac{1}{1+e^{-2x}}

函数曲线变为：

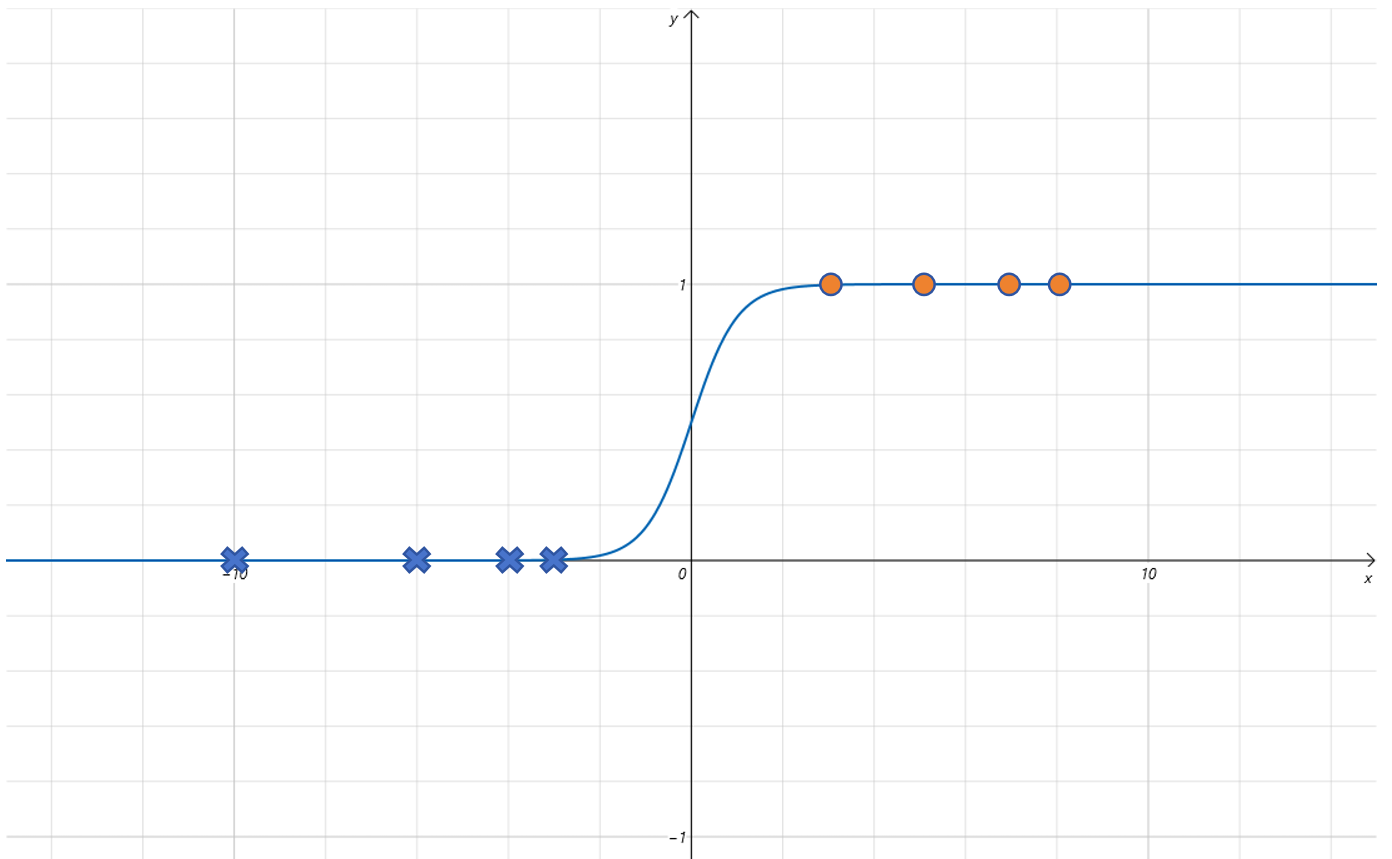
可以发现函数曲线沿着x轴方向压缩了。这样更能拟合我们之前的点了。

所以增加一个可以训练调整的参数w，就可以让模型更加拟合数据。

7.1.3复习时间与是否挂科

再看一个例子，考试前，大家都在为考试进行紧张的复习，你统计了大家的复习时长和最终是否挂科。数据如下：

复习时长	是否挂科
20	0
3	1
13	0
7	1
15	0
5	1
17	0
9	1

绘制上边数据的图像如下：

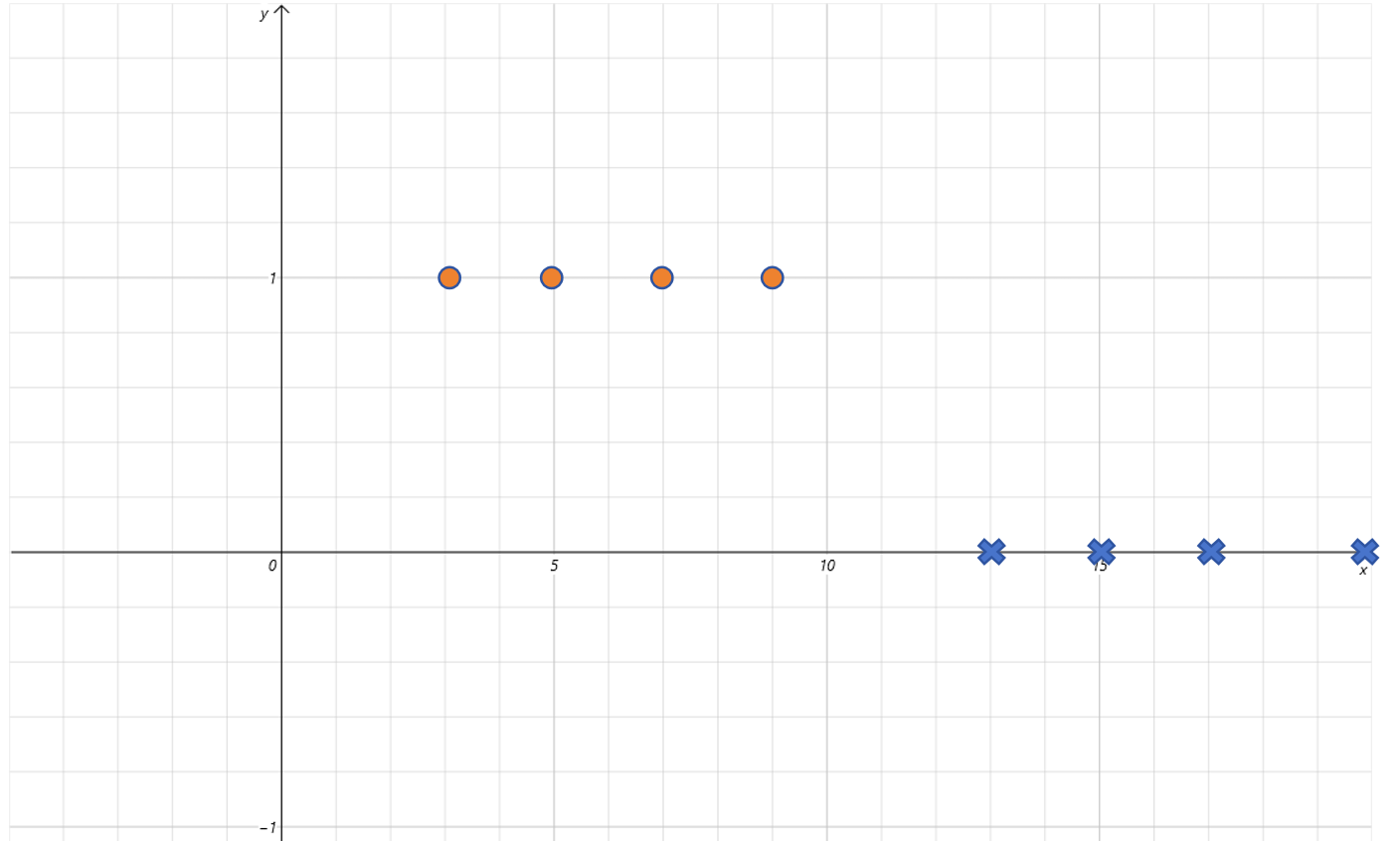
首先我们发现，这些数据点是左高右低，也就是x取值较小的部分，Label值为1，x取值较大的部分，Label值为0。这和Sigmoid左低右高刚好的相反的。不过没关系，我们已经给Sigmoid函数增加了参数w。我们可以让w为负值来解决这个问题。比如让w为-2：

sigmoid(-2x)=\frac{1}{1+e^{2x}}

对应的函数曲线如下：

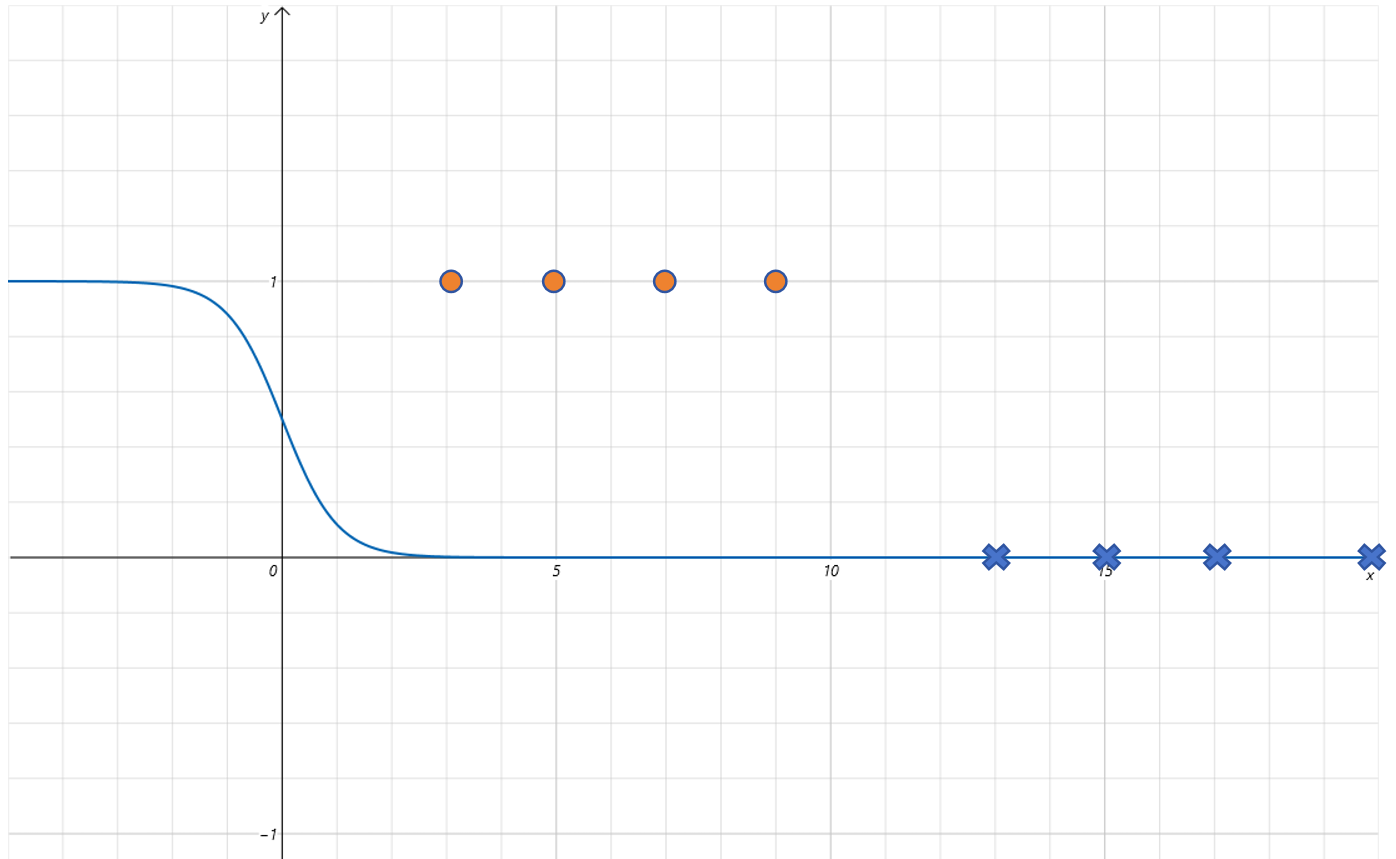
7.1.4给Sigmoid函数增加平移参数

根据上边图像看，我们还需要对Sigmoid函数进行平移才可以拟合这些点，那我们就给Sigmoid函数再增加一个参数b。

sigmoid(wx+b)=\frac{1}{1+e^{-(wx+b)}}

然后，我们设置w为-2，b为22时：

sigmoid(-2x+22)=\frac{1}{1+e^{2x-22}}

拟合曲线为：

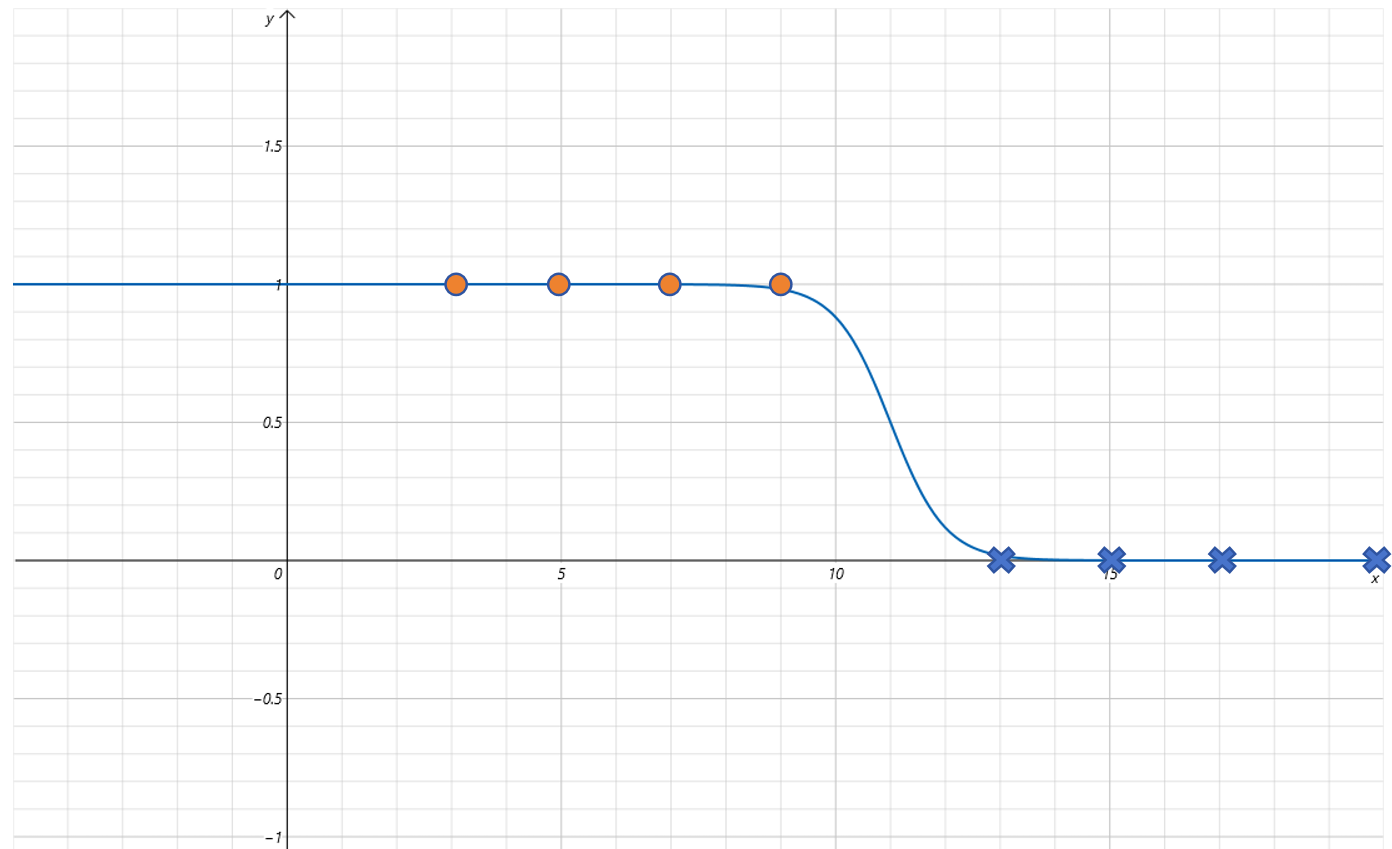
可以发现对Sigmoid函数增加w和b参数就可以很好的拟合这些点了。后边我们会训练模型，让模型自己找到合适的w和b的值。

7.1.5一元逻辑回归的假设函数

通过上边的学习，我们知道一元逻辑回归模型的假设函数为：

LogisticRegssion(x) = Sigmoid(wx+b)=\frac{1}{1+e^{-(wx+b)}}

其中的w和b参数会对标准的Sigmoid函数曲线进行平移，翻转，缩放等。将x映射到[0,1]。

7.1.6逻辑回归的预测

当你有一个训练好的逻辑回归模型，它的输出是Sigmoid函数的输出，范围是0-1之间，正好是概率值的范围。越接近1，证明这个样本越接近正例。一般默认以0.5作为决策临界值。大于等于0.5则认为是正例，小于0.5则认为是负例。当然你也可以调节这个决策临界值，比如改为0.6，这样你对模型预测的正例就更有把握。但同时可能有一些正例会被你误判为负例。

7.1.7对一元逻辑回归的理解

我们对Sigmoid函数的输入x，增加了w和b参数。实际上就是对x应用了一个线性回归，然后再进行Sigmoid变化。

所以我们可以理解为一元逻辑回归就是在线性回归的基础上，增加了一个Sigmoid函数。这个Sigmoid函数叫做激活函数。在深度学习里，输入首先经过一个线性变化，然后经过一个非线性的函数，比如这里的Sigmoid函数。这个非线性的函数我们就叫做激活函数。激活函数的作用就是在线性函数的基础上增加了非线性。Sigmoid函数是我们学习的第一个激活函数。它在输入小于0的时候，对输出产生抑制作用，输出接近于0,当输入大于0时，产生激活作用，输出快速接近1。

一元逻辑回归