7.2逻辑回归的损失函数

构建一个模型，就是寻找一个假设函数。也就是你认为输入和输出符合的关系。对于2分类问题，也就是将输入映射到0和1的函数，我们已经找到了那就是：

LogisticRegssion(x) = Sigmoid(wx+b)=\frac{1}{1+e^{-(wx+b)}}

训练一个模型，就需要定义损失函数，然后利用梯度下降算法，让损失越来越小。最终得到让损失最小的模型参数。

预测就是利用训练好的模型参数和新采集的Feature，带入假设函数，预测一个输出。

上一节我们学习了逻辑回归的假设函数，这一节，我们来研究逻辑回归的损失函数。

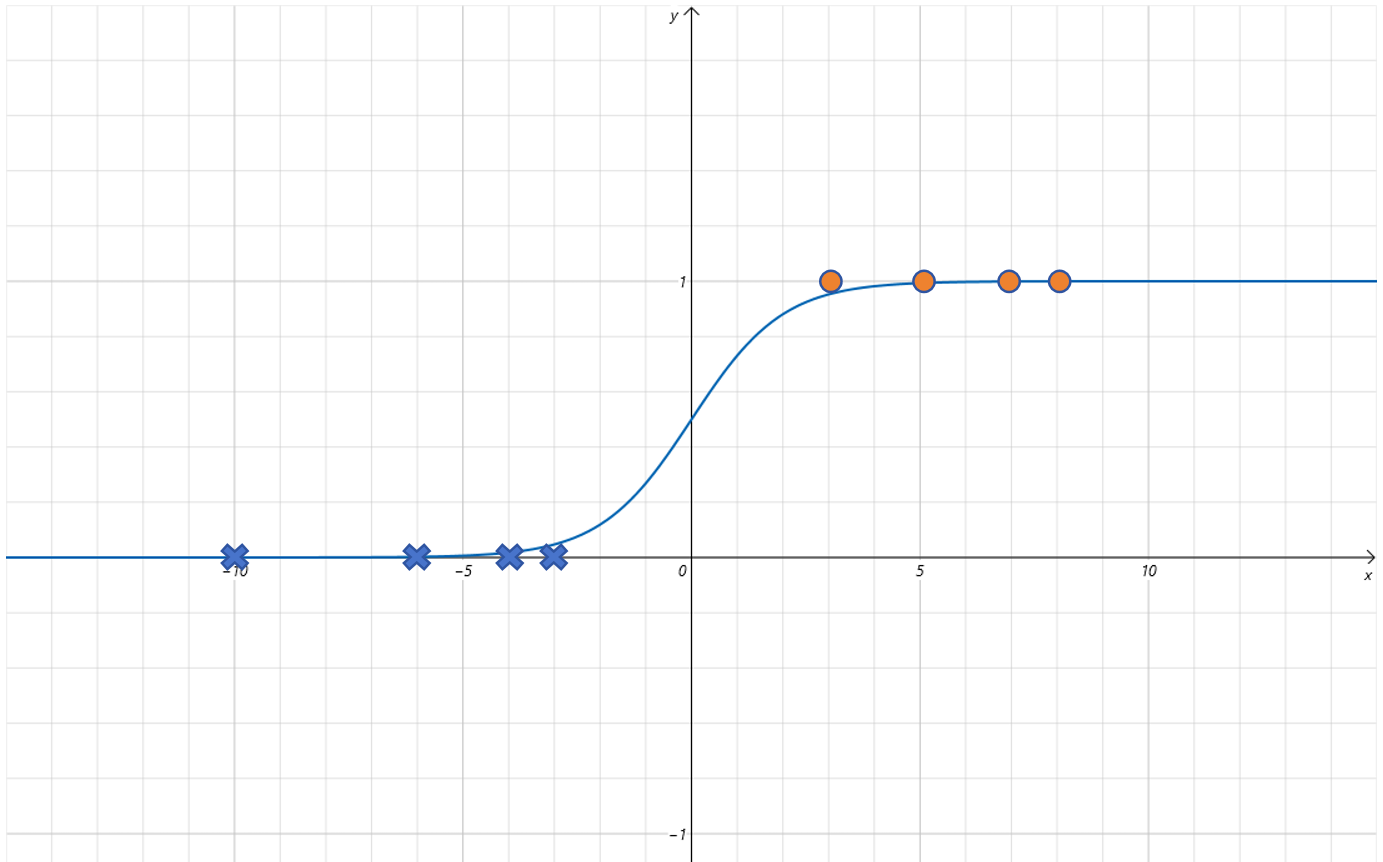
之前线性回归时我们利用的均方误差MSE作为损失函数。我们可以试一试逻辑回归是否也可以利用MSE作为损失函数。

将上边的数据带入MSE函数，绘制loss图像如下，其中Z轴为loss值，X轴为w，Y轴为b。

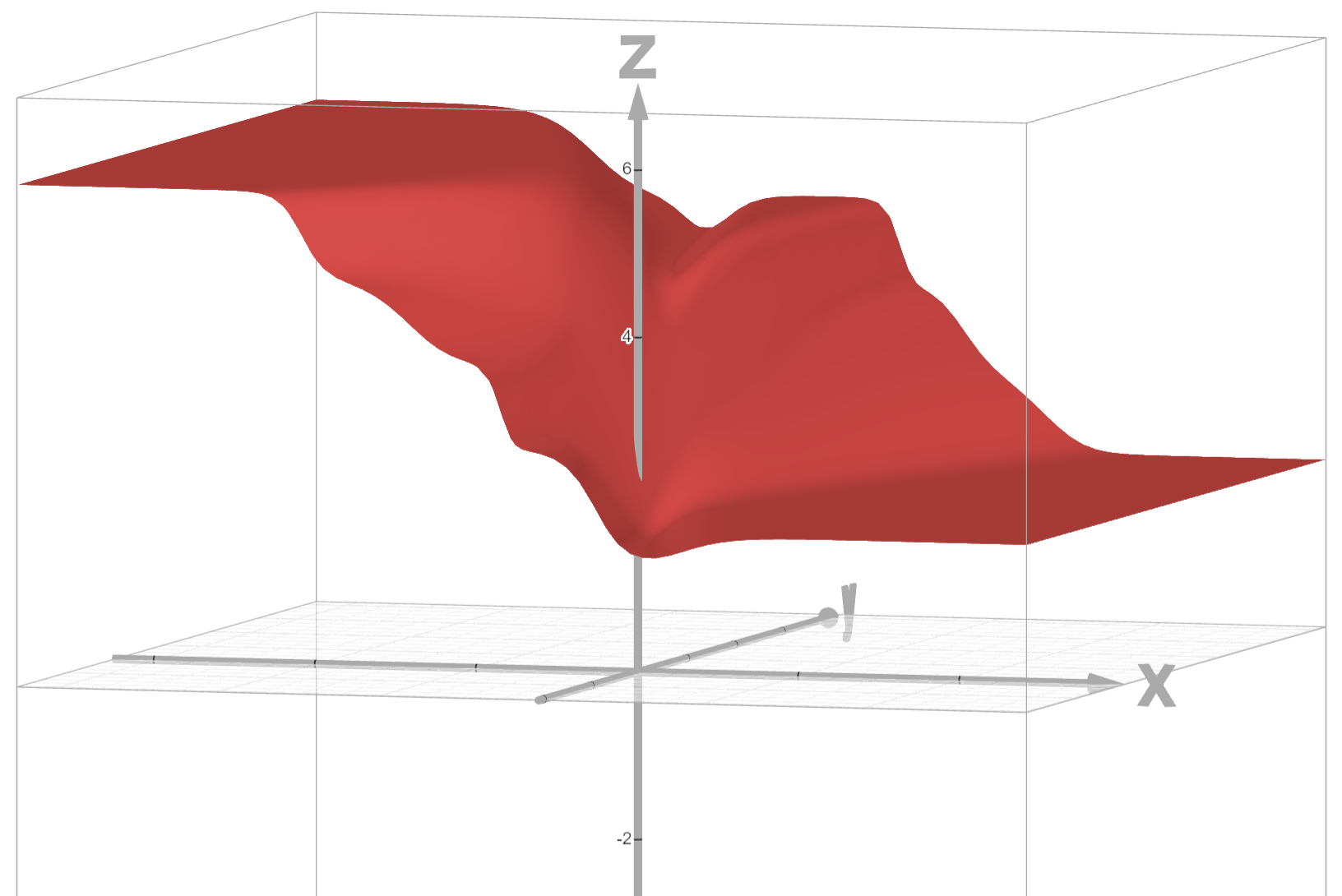
通过观察发现，它是一个非凸函数，也有很多局部最小值。训练起来非常不稳定。所以我们需要给逻辑回归模型寻找其他的损失函数。

我首先给出二分类交叉熵损失函数，然后我们再来讨论它的性质。

我们用 $y$ 表示Label值，用 $\hat{y}$ 表示预测值。

则二分类交叉熵损失函数BCELoss(Binary Cross Entropy Loss)分为两种情况。

分别是当 $y=1$ 时：

BCELoss=-log(\hat{y})

当 $y=0$ 时：

BCELoss=-log(1-\hat{y})

我们结合函数图像来对BCELoss进行理解：

分别是当y=1时，BCELoss的函数曲线为：

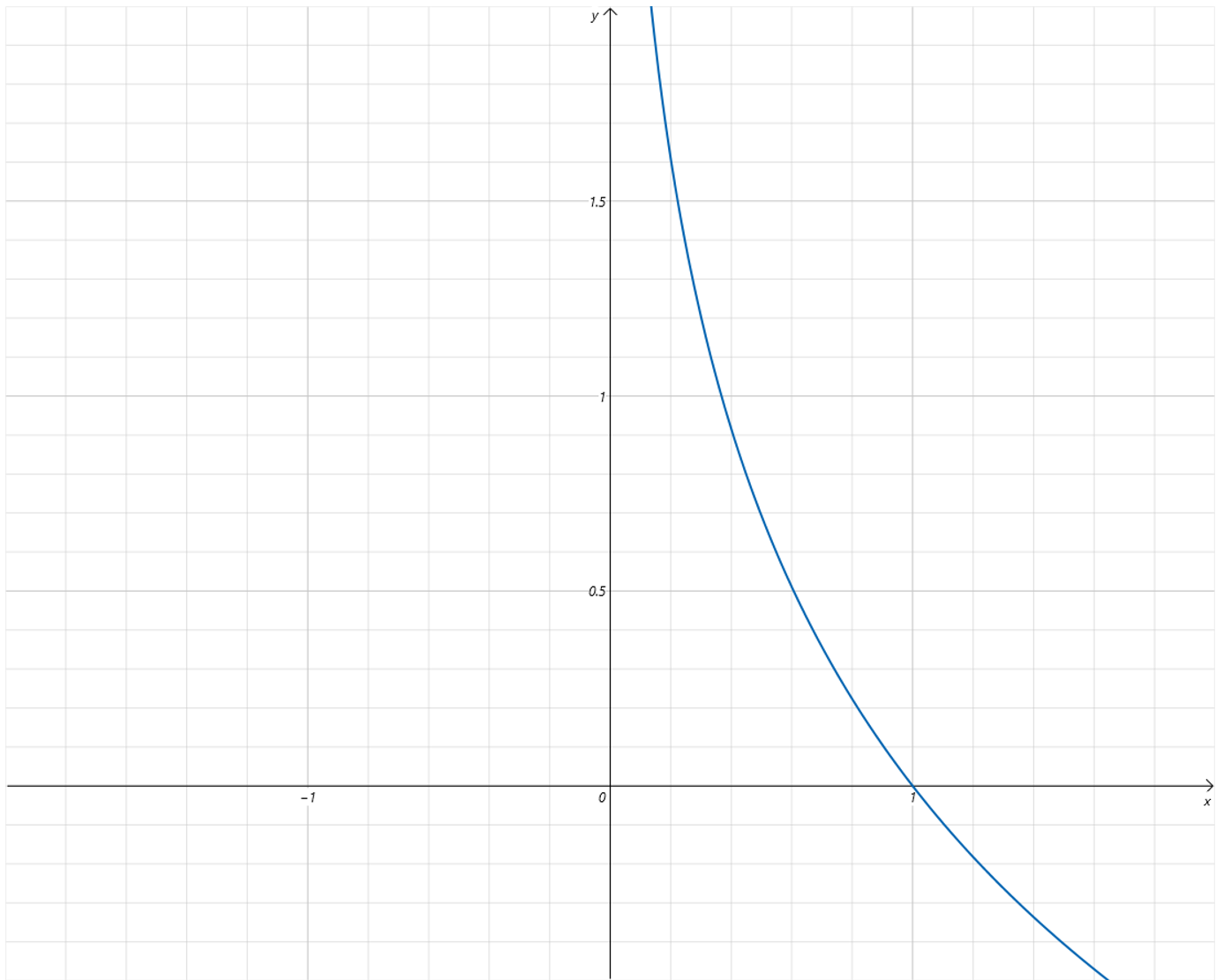
因为Label值为1，预测值为Sigmoid函数的输出，取值为从0到1。从Loss曲线可以看到，当预测值越接近0，Loss值越大，越接近1，Loss值越小。当预测值和Label相等，等于1时，Loss值为0。

当y=0时，BCELoss的函数曲线为：

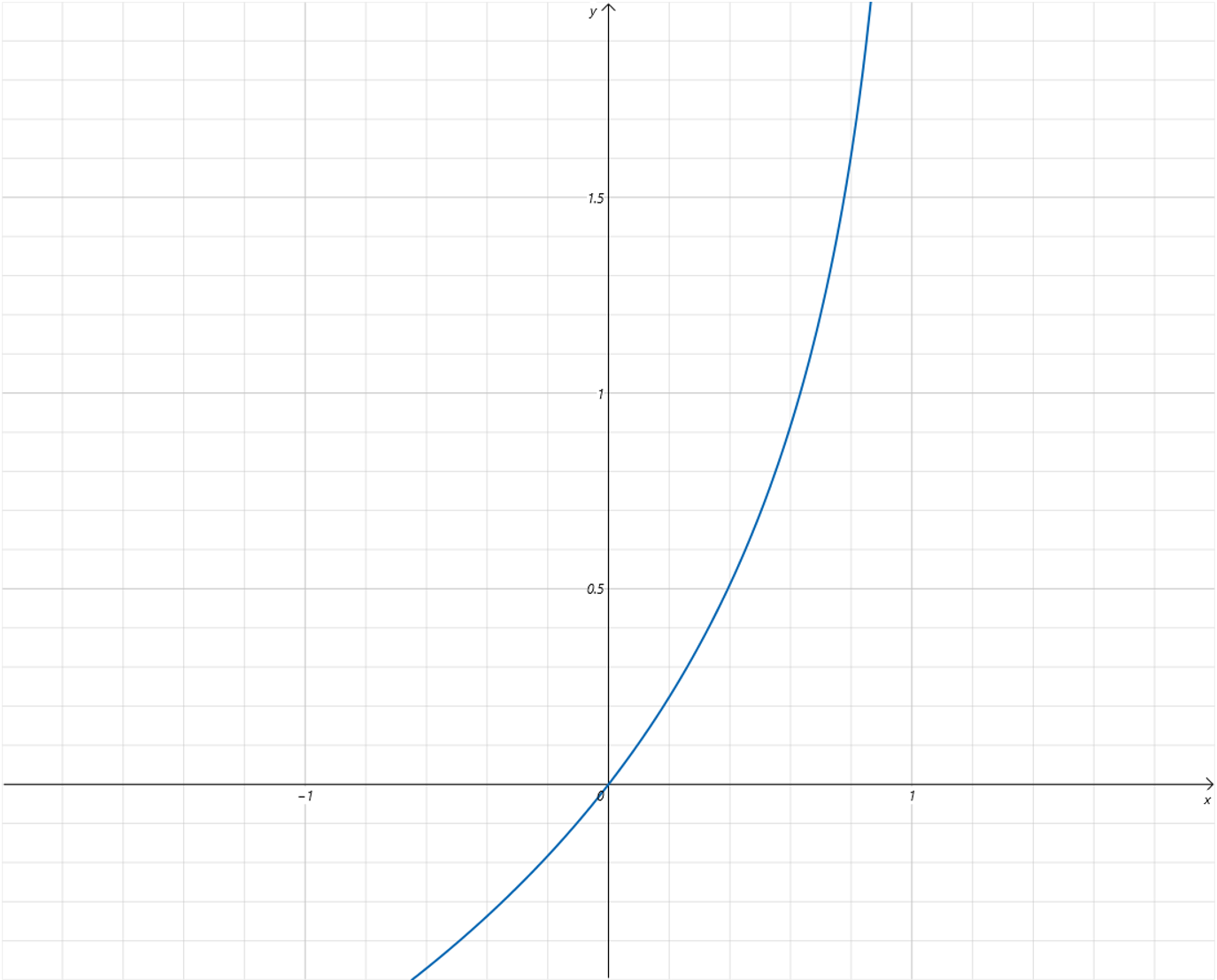
因为Label值为0，预测值为Sigmoid函数的输出，取值为从0到1。从Loss曲线可以看到，当预测值越接近1，Loss值越大，越接近0，Loss值越小。当预测值和Label相等，等于0时，Loss值为0。

BCELoss需要分情况来写，比较麻烦，我们将它们统一到一个式子里：

BCELoss(y,\hat{y}) = -[ylog\hat{y}+(1-y)log(1-\hat{y})]

你可以分别将y=1和y=0的两种情况y的值分别带入，BCELoss的表达式和上边分情况讨论的表达式是完全一样的。

我们之前不采用MSELoss是因为它的函数图像不够平滑，那我们看一下BCELoss的函数图像。我们绘制出上边那个简单例子的BCELoss的图像来看一下：

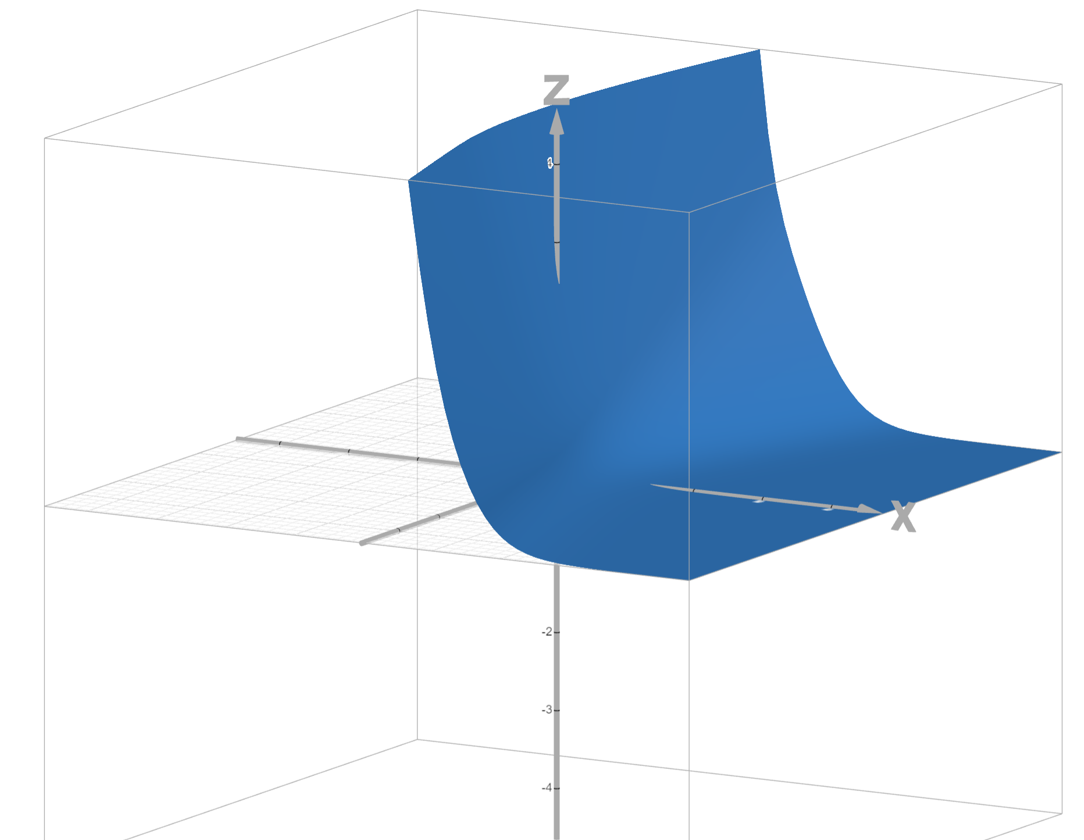
可以看到它的函数图像非常平滑，非常适合用梯度下降来优化。

逻辑回归的损失函数