3.1 函数的极限

3.1.1 宇宙是无穷大的

我第一次得知宇宙是无穷大，是在我初中的一堂课上。老师告诉我们说：“什么是无穷大？无穷大就是不论你认为宇宙多大，它比你想的还要大！” 这句话对当时的我造成了很大的震撼。一方面是宇宙竟然没有边。另一方面是老师这种对无穷大的奇妙表达方式。以至于到现在我还清楚的记得这句话。

3.1.2 函数趋于无穷大的极限

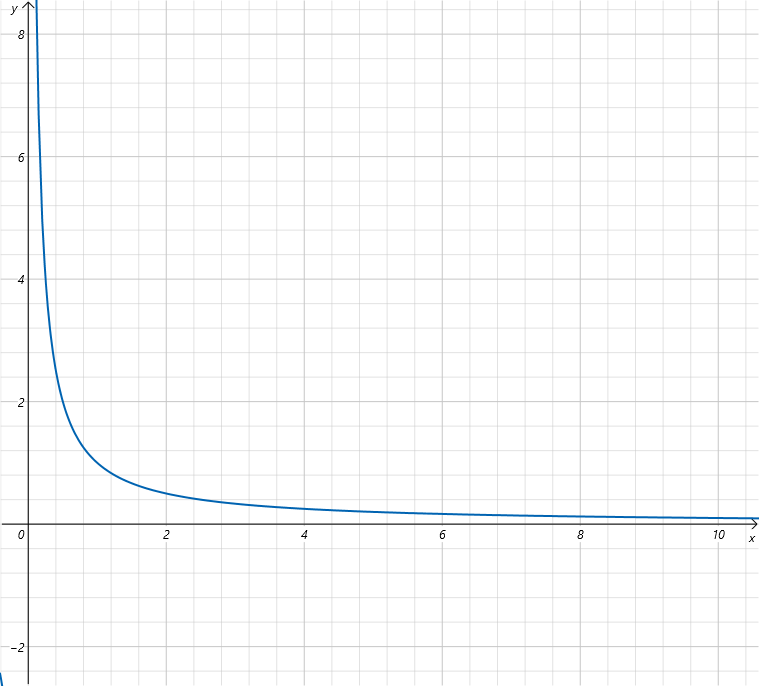
对于如下函数用数学语言如何定义在自变量趋于正无穷大时它的极限：

则称$x \to +\infty$时，$f(x)$的极限为$A$，记作：

为了帮助你理解，用我初中老师的话来说就是，存在一个数$A$，不论你想到一个数$\varepsilon >0$多小，总存在一个$x_0$,$f(x)$在自变量$x>x_0$时的值与$A$之间的绝对差值，比你想的还要小。那么$A$就是函数$f(x)$趋于正无穷大时的极限。

函数趋于负无穷大时与正无穷大类似，我们不再赘述。

3.1.3函数趋于一点时的极限

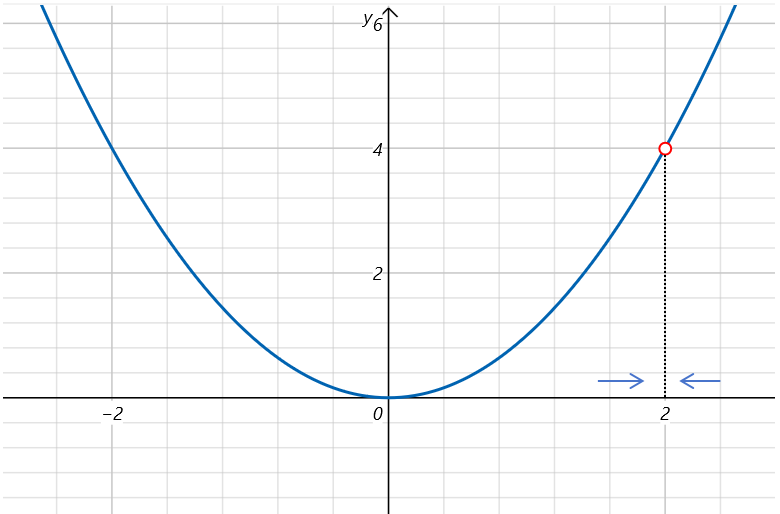
以函数$f(x)=x^2$为例，我们规定x的定义域为不等于2的实数。那么当x趋于2时，$f(x)$的极限是怎么定义呢？

设$f(x)$在某去心邻域有定义，存在实数$A$，对于任取$\varepsilon >0$，存在 $\delta>0$，使得$0<|x-x_0|<\delta$时有：

则称$x \to x_0$时，$f(x)$的极限为$A$，记作：

3.1.3 无穷小和高阶无穷小

无穷小

无穷小是指在某个极限过程中趋于0，但不等于0的量。 例如：

当x趋于0时，x是无穷小。

当x趋于0时，$x^2$也是无穷小。

高阶无穷小

当多个无穷小进行比较时，我们可以通过“趋近于零的速度”来判断他们的“阶”：

若$f(x)$和$g(x)$都是无穷小，且：

则说$f(x)$是比$g(x)$高阶的无穷小。

比如：

我们就说当x趋于0时， $x^2$是$x$的高阶无穷小。换句话说就是：当x趋于0时， $x^2$比$x$更快的趋于0。一般用符号$O(x)$表示x的高阶无穷小。