15.4位置编码

序列问题最主要的特征就是数据的顺序是非常重要的，如果数据交换顺序，那么表达的含义就会发生改变。比如对于两个文本序列“狗咬人”和“人咬狗”，token都一样，但是序列不同意思不同。之前RNN是通过顺序读入序列数据来保障的，但是之前我们看到Transformer只用注意力来更新token的embedding。并且所有token可以并行计算，进行更新。这其中并没有引入任何token在序列中的位置信息。这一节我们就给token加入位置信息。

15.4.1 绝对位置编码

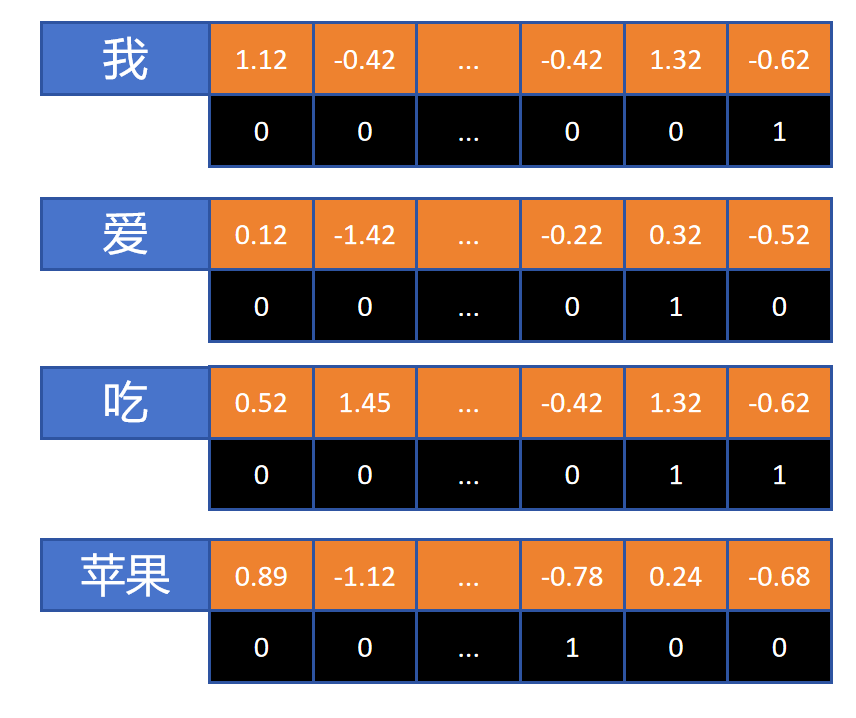我们能想到的最简单的编码方式，那就是绝对位置编码了，比如上图，对每个token设计一个和word embedding一样维度的position embedding。 对于“我爱吃苹果”这句话由4个token构成，它们position embedding的后三位分别为“001”、“010”、“011”、“100”。编码后将word embedding和position embedding按位相加。这样就给每个token的embedding里增加了位置信息。

绝对位置编码有个问题就是训练时的序列长度是固定的，位置编码每个维度的数值只能是0或者1（离散的），如果预测时序列长度超出训练时的长度，模型就无法处理，也不能根据训练时的数据外推到更大的长度。

15.4.2 什么是好的位置编码

一个好的位置编码，应该每个维度都是连续值，这样即使将来出现更长的序列，只需要更大的数字表示就可以。还有一点就是可以借鉴机械表的设计，表有时针，分针，秒针。在计时过程中，秒针变化最快，分针次之，时针变化最慢。且都是周期性变化。

所以我们期望的位置编码是每个维度上的数字都是连续型的。而且位置编码的低维数字变化快，高维数字变化慢，每个维度都为周期性变化。

15.4.3 Sin函数位置编码

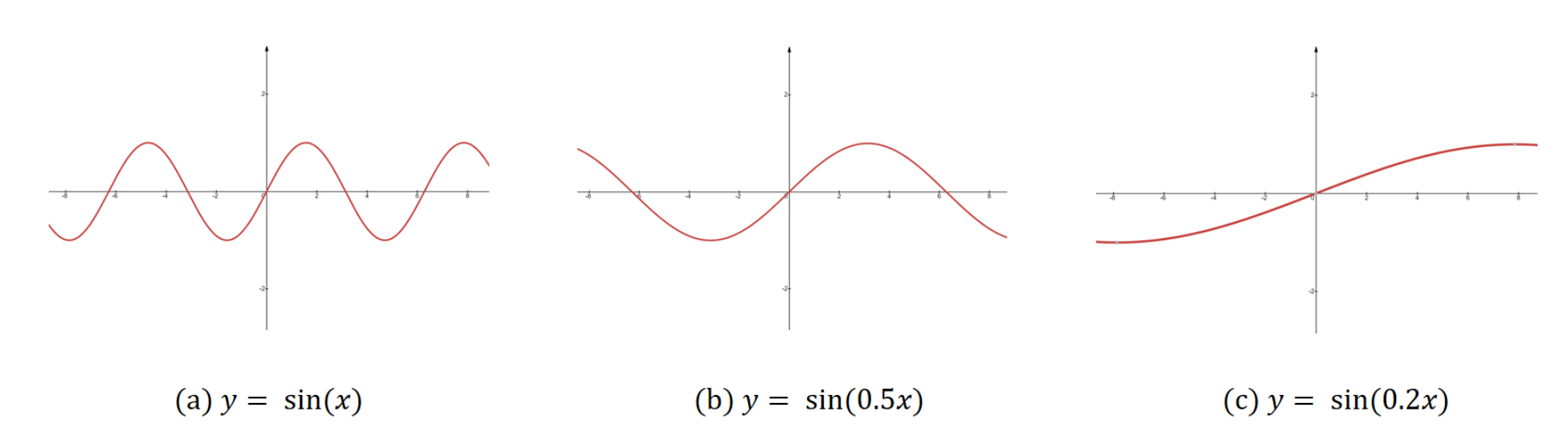通过上图可以看到，sin函数是个周期函数。通过给输入x增加一个系数，可以调节波长，波长越长，函数值随x变化越慢。这样我们就可以用sin函数作为位置编码函数。位置编码的低纬度用波长短的sin函数，这样值的变化快。高纬度用波长长的sin函数，这样值的变化慢。

假设位置编码有3个维度，我们分别用3个sin函数来对3个维度进行编码：sin(x)、sin(0.5x)、sin(0.2x)。其中x代表token在序列中的位置。 则第一个token的位置编码为：

$[sin(1),sin(0.5),sin(0.2)]=[0.84,0.48,0.20]$

第二个token的位置编码为：

$[sin(2),sin(1),sin(0.4)]=[0.91,0.84,0.39]$

对于一个512维的位置编码，我们可以如下定义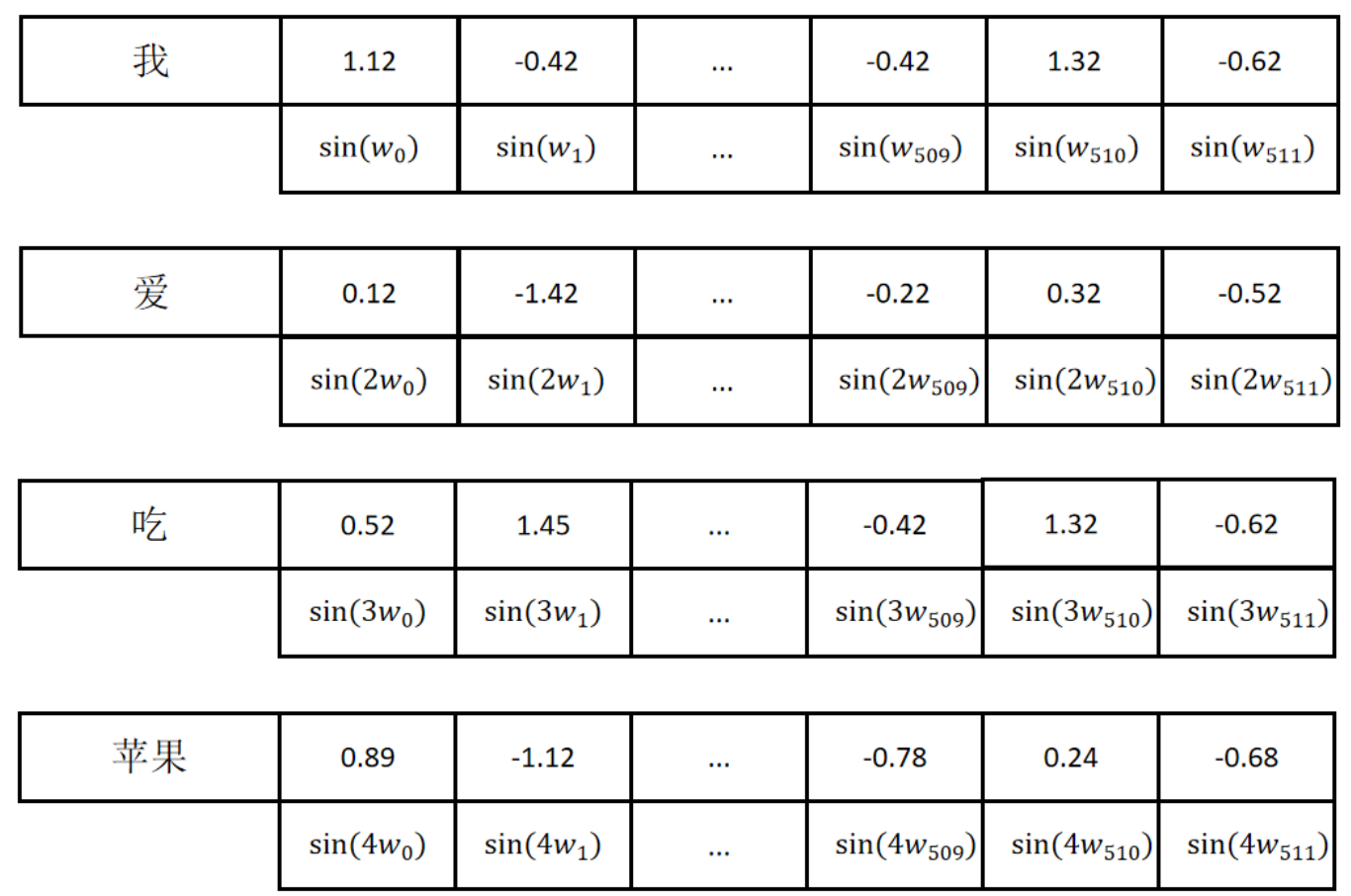： 每个编码位置的sin()函数的系数用$w_i$表示，i从0开始，到feature_size减1。随着编码位置的增加，$w_i$变小，意味着sin()函数的波长变长。

$w_i = \frac{1}{10000^{i/feature\_size}}$

但实际上Transformer里是用sin和cos函数交替来进行编码的。如下图所示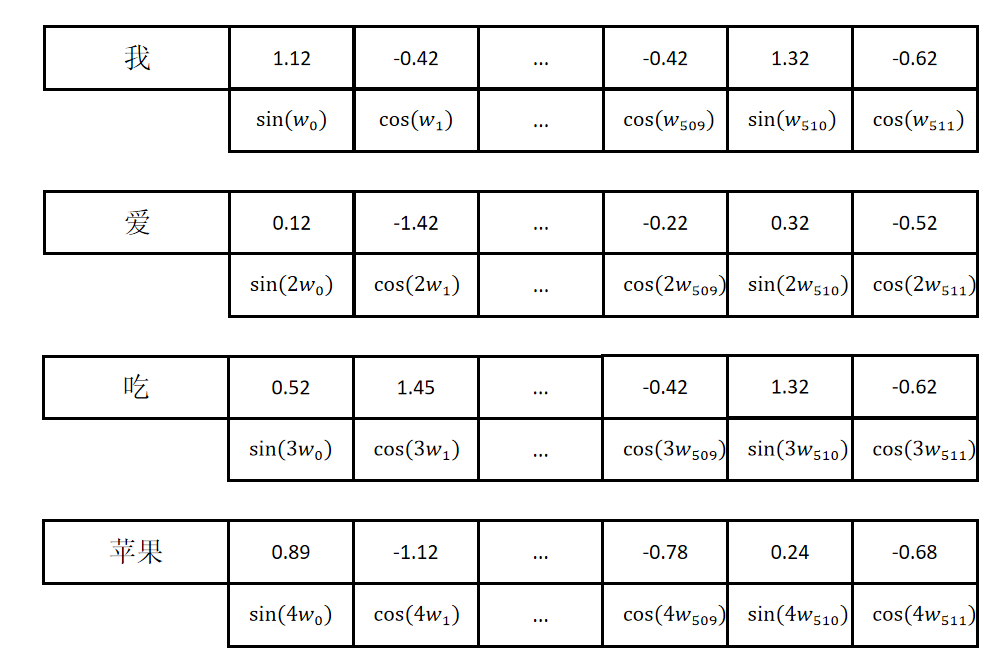： 上图中偶数位置用sin函数系数用$w_{2i}$表示，奇数位置用cos函数，系数用$w_{2i+1}$表示。

$w_{2i}= \frac{1}{10000^{2i/feature\_size}}$

$w_{2i+1}= \frac{1}{10000^{2i/feature\_size}}$

同样sin和cos函数都是随着维度增加波长增加的周期函数，那么入cos函数的好处是什么呢？注意力机制是通过q向量和k向量的点积来计算的。对于用sin和cos交替进行编码的两个位置向量，一个位置是t，一个位置是t加$\triangle t$。对这两个位置编码进行点积运算如下：

$(sin(w_it),cos(w_it))\cdot(sin(w_i(t+\triangle t)),cos(w_i(t+\triangle t))$

$=sin(w_it)sin(w_i(t+\triangle t))+cos(w_it)cos(w_i(t+\triangle t))$

$=cos(w_i(t-(t+\triangle t)))$

$=cos(w_i\triangle t)$

通过上边计算可以看到最后注意力计算结果只与两个位置之间的相对位置$\triangle t$有关，而和绝对位置t无关，这对于自然语言处理是非常重要的，因为一个词组的意思只和这个词组里单个字之间的相对位置有关，而和这个词出现在句子里的绝对位置无关。

15.4.4 PyTorch实现位置编码

class PositionalEncoding(nn.Module):

    def __init__(self, d_model: int, seq_len: int, dropout: float) -> None:
        super().__init__()
        self.d_model = d_model
        self.seq_len = seq_len
        self.dropout = nn.Dropout(dropout)
        # 创建一个空的tensor
        pe = torch.zeros(seq_len, d_model)  # (seq_len, d_model)
        # 创建一个位置向量
        position = torch.arange(0, seq_len, dtype=torch.float).unsqueeze(1)  
        # 计算分母
        div_term = torch.pow(10000.0, -torch.arange(0, d_model, 2, dtype=torch.float) / d_model)  # (d_model / 2)
        # 偶数位调用sin
        pe[:, 0::2] = torch.sin(position * div_term) 
        # 奇数为调用cos
        pe[:, 1::2] = torch.cos(position * div_term) 
        # 增加batch维度
        pe = pe.unsqueeze(0)  # (1, seq_len, d_model)
        # 注册位置编码为一个buffer，这个tensor不会参与训练，但是会随同模型一起被保存或者迁移到GPU。
        self.register_buffer('pe', pe)

    def forward(self, x):
        x = x + (self.pe[:, :x.shape[1], :]).requires_grad_(False) 
        return self.dropout(x)