5.2 给线性回归加上偏置

5.2.1 直线方程

我们知道平面上的直线方程为：

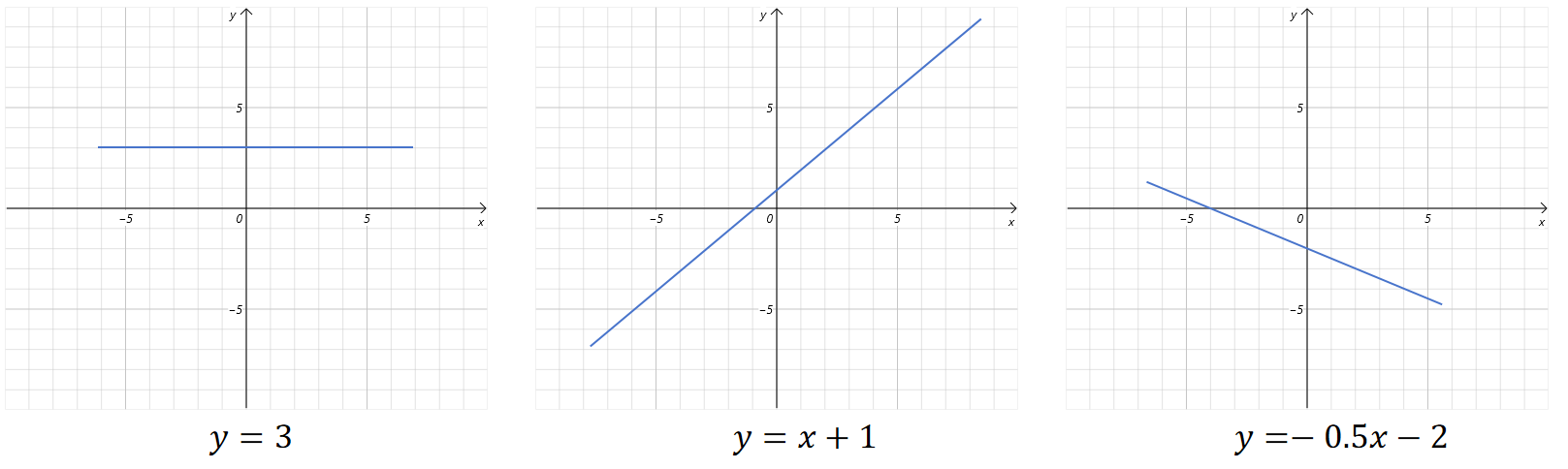
通过给w和b设置不同的值，可以生成不同的直线。

我们把b称为偏置，也可以叫做截距。

5.2.2 加上偏置

上一节，为了简化计算，我们的线性回归假设b等于0，也就是直线肯定通过原点。这一节，我们将b也设置为一个可以训练的参数。看看对预测有什么影响。

训练数据：

线性函数：

在机器学习里，有时也将用来拟合数据的函数称为假设函数，因为这个函数包含了你的假设，比如这里，你认为feature（温度）和label（销量）之间满足线性关系。

损失函数：

我们带入训练数据有：

$loss =(60-10w-b)^2+ (85-20w-b)^2+(100-25w-b)^2+ (120-28w-b)^2$

$+(140-30w-b)^2+ (145-35w-b)^2+(163-40w-b)^2$

通过化简有：

$loss=5634w^2+7b^2-47910w-1626b+376wb+102419$

w为x轴，b为y轴，loss为z轴，绘制图像如下：

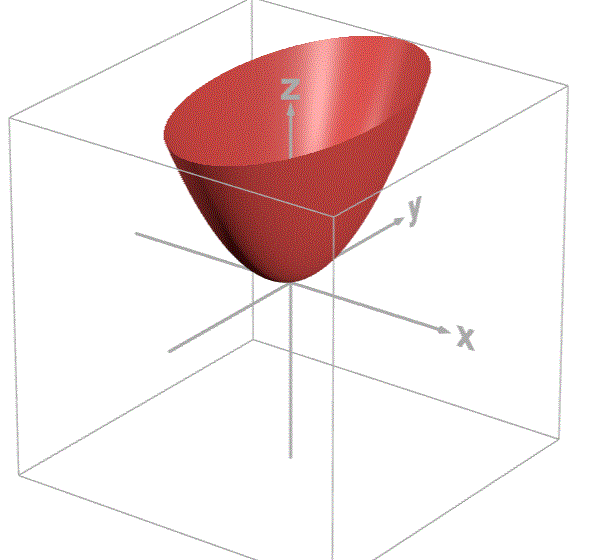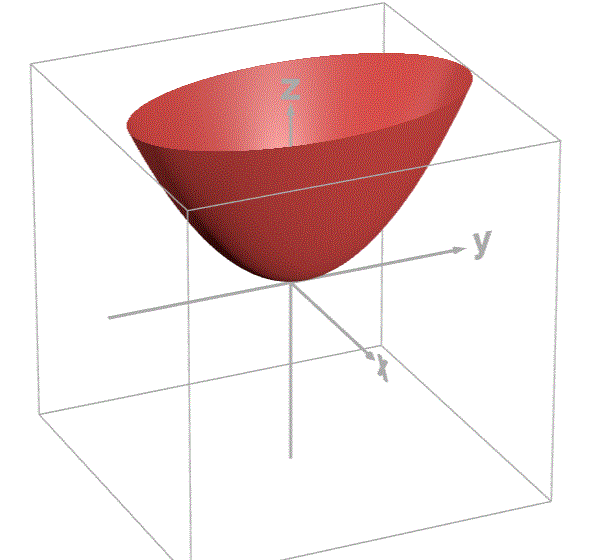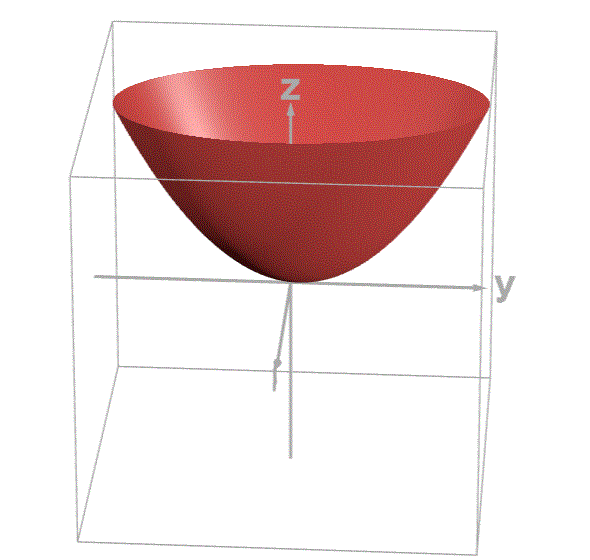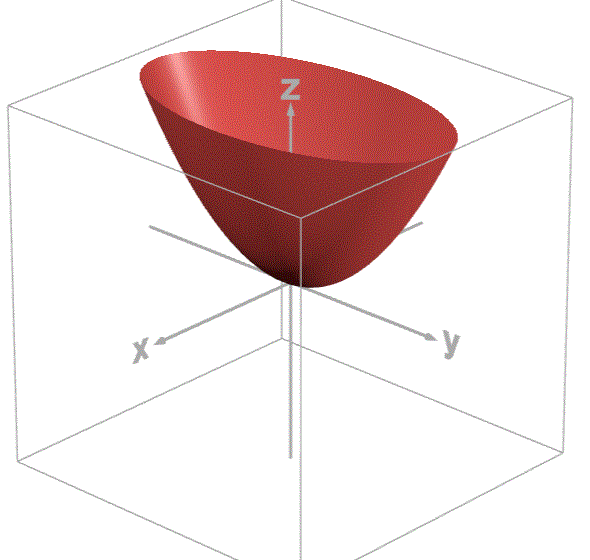
通过观察图像可知，loss有最小值，根据之前学习偏导数的知识可知在loss取最小值时，loss对w和对b的偏导数都为0。所以，我们用loss分别对w和b求偏导，并让偏导数等于0。联立方程，从而求出loss最小值时w和b的取值。

loss对w求偏导，并让偏导等于0：

联立两个方程，求出w，b，最终得到：

最终拟合训练数据的直线就为：

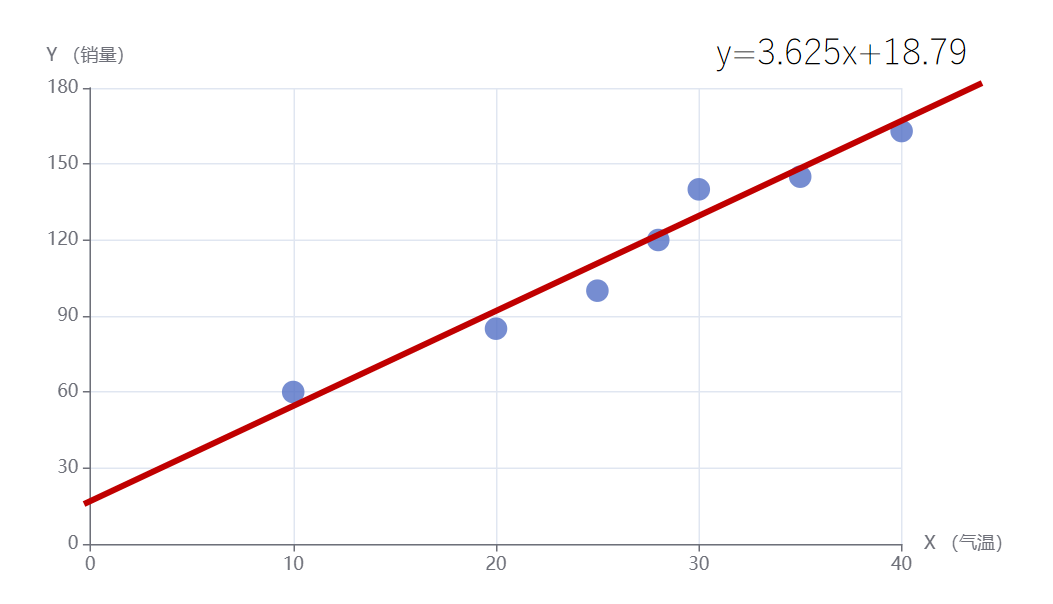
可以看到这个直线不通过原点，它更加拟合这些点。通过计算，所有点的累积误差平方和为309.21。而上一节没有偏置的线性回归，累积误差平方和为565.625。可以看到，通过加入偏置后的线性回归模型误差减小了不少。