5.1 一元线性回归
5.1.1 预测冰激凌销量

夏日里,烈日炎炎,你在路边售卖冰淇淋。你根据经验发现,气温越高,销量越好。于是你想是否能根据天气预报明天的气温,准确预测明天冰激凌的销量呢?
你收集了下边一组数据:
| 温度 | 销量(个) |
|---|---|
| 10 | 60 |
| 20 | 85 |
| 25 | 100 |
| 28 | 120 |
| 30 | 140 |
| 35 | 145 |
| 40 | 163 |
将这些点绘制出来,形成一个散点图。
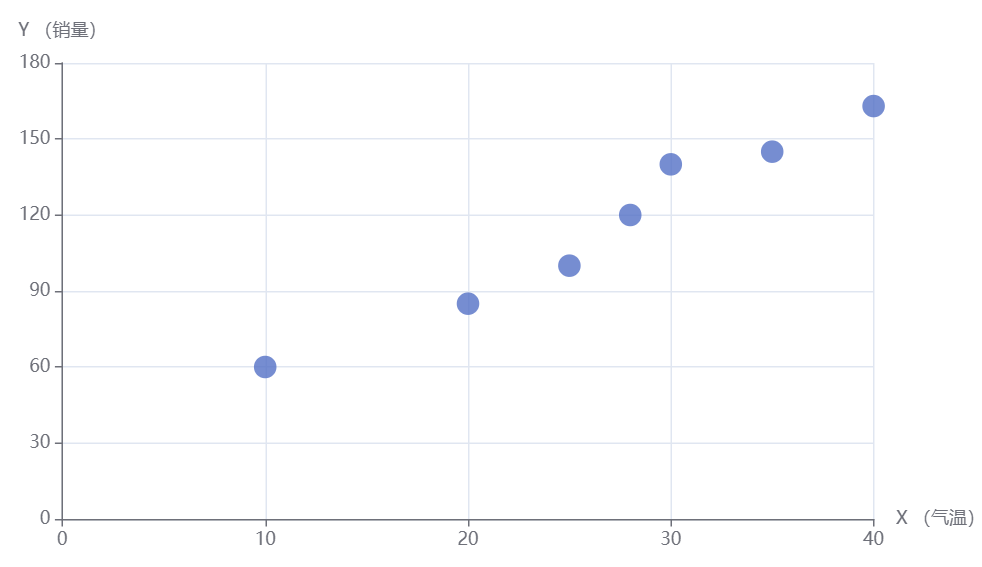
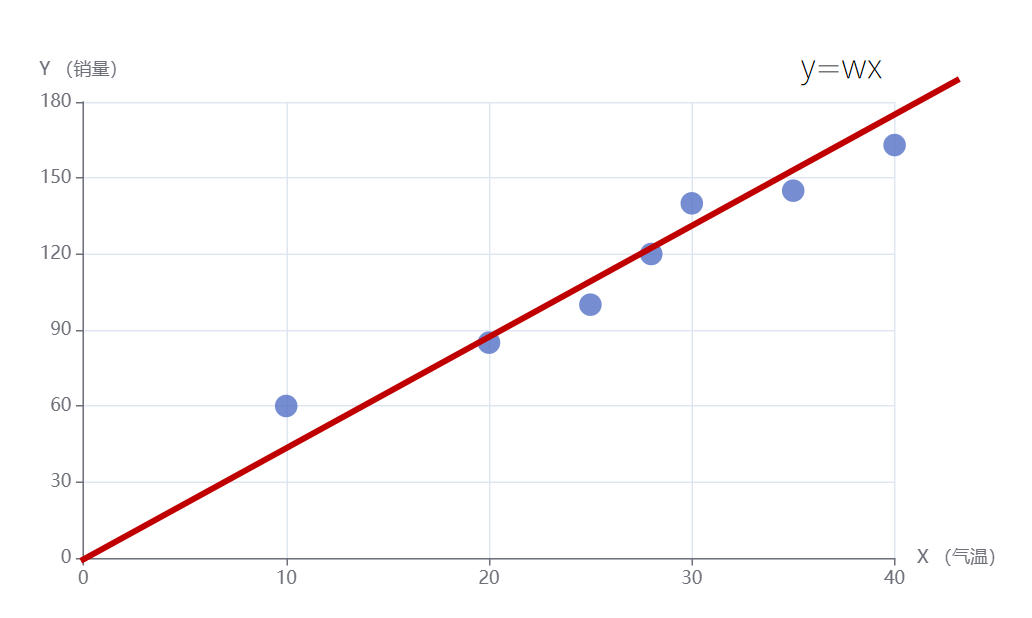
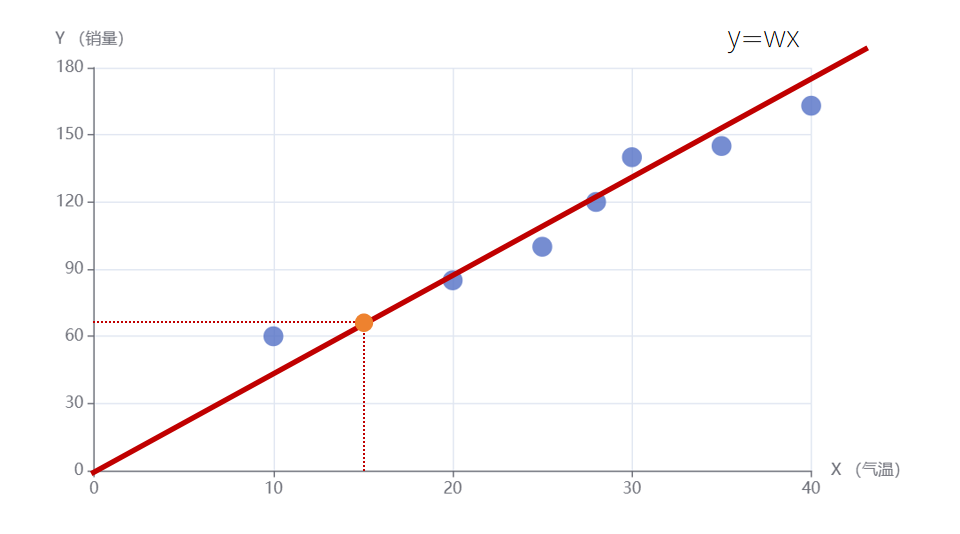
5.1.2 通过数学方法拟合
上边我们是通过观察的办法来得到这条拟合直线的,那如何让程序来帮我们找到这条直线呢?
我们上边通过观察拟合直线的原则是让所有点距离拟合直线最近。换句话说就是误差最小,下边我们就来严格定义一下误差。
在深度学习里我们把收集到的真实数据叫做样本,样本里的输入叫做特征(feature),我们要预测的值叫做标签(label)。深度学习的模型就是一个函数,这个函数的输入是样本的feature,输出是预测值。训练过程就是调节函数内部的参数(Parameter)(也可以叫做权重(weight)),来让预测值尽可能的接近label。当模型训练好之后,就可以只输入新的样本的feature,模型根据学习到的内部参数,计算出预测值了。
比如对于训练数据里的第一个样本点,feature为气温x,值为10,label为销量y,值为60。假设我们拟合一个通过原点的直线为y=4x。那么带入x的取值10,得到预测的y值为40。那么这里预测值40和label值60之间就产生了一个误差。然后将所有点的误差都累积起来,能让累积误差最小的直线,就是最好拟合我们数据的直线。因为误差有正有负,所以我们取每个点误差的平方再累加,作为最终累积误差。
样本点的label(销量)我们用y来表示,通过直线预测的销量用来表示。表示第i个样本点的label。表示第i个预测的销量值。则误差平方和就可以表示为:
在深度学习里,我们把上式叫做损失函数,损失函数就是衡量预测值和真实值(label)之间的差距的。模型训练的目的就是降低loss。 拟合直线里有一个可以训练的参数w,预测值可以表示为:
将式5-2带入式5-1则有:
因为训练数据的样本点都是已知的。 我们将实际数据带入上式有:
绘制上边关于w的图像为:
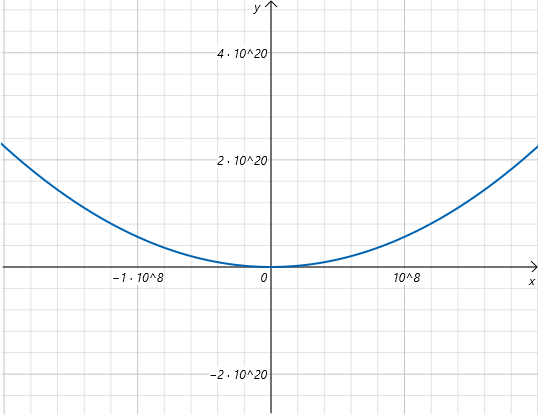
其中y轴是loss值,x轴是直线斜率w的值。我们只需要取loss最低时对应的w就可以得到我们期望的拟合直线了。但是因为x轴和y轴数值都非常大,我们很难通过观测得到最低点的值。
根据之前我们学过导数的性质,如果一个函数存在极值,那么它的导数为0。我们让loss函数对w求导,并让导数等于0。从而求解出w。
所以我们要找的最佳拟合直线就为:
。
将4.25带入损失函数,我们可以计算出总体累加损失为565.625。
5.1.3 线性回归
通过本节我们学会了如何针对一组点,找出最佳的拟合直线了。这个算法就叫做线性回归。
线性回归就是假设样本的feature和label之间满足线性关系,线性回归模型训练过程就是找到能让损失函数值最小的,斜率w的值。当然,这里我们没有训练模型,而是通过直接求解得到w的最优值。后边我们会讲如何通过训练模型得到w的最优值。
为什么叫做回归?
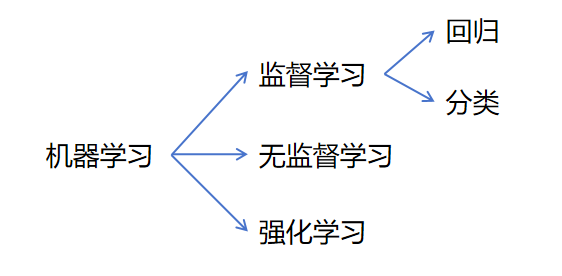
在机器学习里的算法分为监督学习算法,无监督学习算法,强化学习算法。
监督学习:
在监督学习中,数据集中每个样本都有输入特征(X)和对应的标签(Y)。算法通过学习数据中的输入-标签关系来进行预测。机器学习中大部分的算法都是监督学习,比如我们刚才讲的线性回归。还有比如你要让模型通过宠物照片识别照片中是猫还是狗,你提供给模型的训练数据里,必须包含人标注的数据。也就是通过label告诉模型每个训练照片是猫还是狗,让模型学习特征和标签之间的关系。
无监督学习:
在无监督学习中,数据集中只有输入特征(X),没有标签(Y)。算法自动发现数据中的模式对数据进行分析。无监督学习最常见的模型就是聚类模型,比如电信运营商根据所有用户的消费数据,让模型自动发现用户的消费习惯,有的是电话多,有的是流量多,从而聚类出很多套餐类别。在这里并不需要标注数据,只有输入特征,让算法自己去寻找数据里的规律。
强化学习:
在强化学习里,无法直接给出输入特征(X)对应的标签(Y),而只能给出特征对应的奖励值(R)。模型在训练过程中,不断优化参数,追求更高的奖励。比如你用强化学习训练一个下围棋的模型,针对每一步你无法给出下一步棋下在哪里最好,但是却可以通过棋局最终的输赢的子数来给模型每一步设定奖励值。
在监督学习里,又主要分为回归和分类两种算法。
回归:
当你要预测的变量是连续型变量,那么这个算法就是回归算法。比如预测一个人的身高,体重,收入等。
分类:
当你要预测的变量是可数的离散型变量,那么这个算法就是分类算法,比如预测一张宠物图片是猫还是狗。
分类很好理解,就是根据特征对实例进行分类。那预测连续型变量为什么叫做回归呢?
“回归”这个词的由来与统计学中的“回归到均值”概念有关。高尔顿在研究遗传学时观察到,父母身高很高(或很矮)的子女,其身高往往更接近于总体的平均身高。这种现象被称为“回归到均值”。为了描述这种现象,高尔顿提出了“回归”这个术语。
高尔顿在分析父母和子女身高的关系时,试图通过一条直线来描述它们之间的趋势。后来,他的学生卡尔·皮尔逊(Karl Pearson)将这种方法推广并正式发展为统计学中的线性回归模型。
后来人们逐渐将所有对连续型变量预测的算法都叫做回归算法。