18.1 MOE

MOE（Mixture of Experts）是混合专家模型的英文缩写。与MOE大模型对应，我们之前讲的大模型都是稠密（Dense）大模型。在训练一个大模型时，达到同样的性能时，大参数量的模型训练花费更少。我们之前讲过Llama模型训练的哲学是，用大量数据，在训练时花费更大的代价，让小参数量的模型达到一个尽可能好的表现。虽然训练一个同等性能的小参数量模型不如训练一个大参数量模型划算。但是因为训练只有一次，但是推理是无数次。小参数量模型在推理时的花费少，足以弥补训练时的额外花费。

MOE模型的特点是训练时花费代价很小，推理时花费的代价也很小。

18.1.1 MOE模型架构

我们首先来复习稠密大模型里的一个Block。 MOE就是对其中的FeedForwardLayer全连接模块进行了改造，上图展示了全连接模块的内部结构。全连接模块是对每个token进行应用的。假设token的维度是4096，一般稠密大模型的全连接模块都是先升维到原来的4倍：16384，然后再降维到4096。如上图所示。

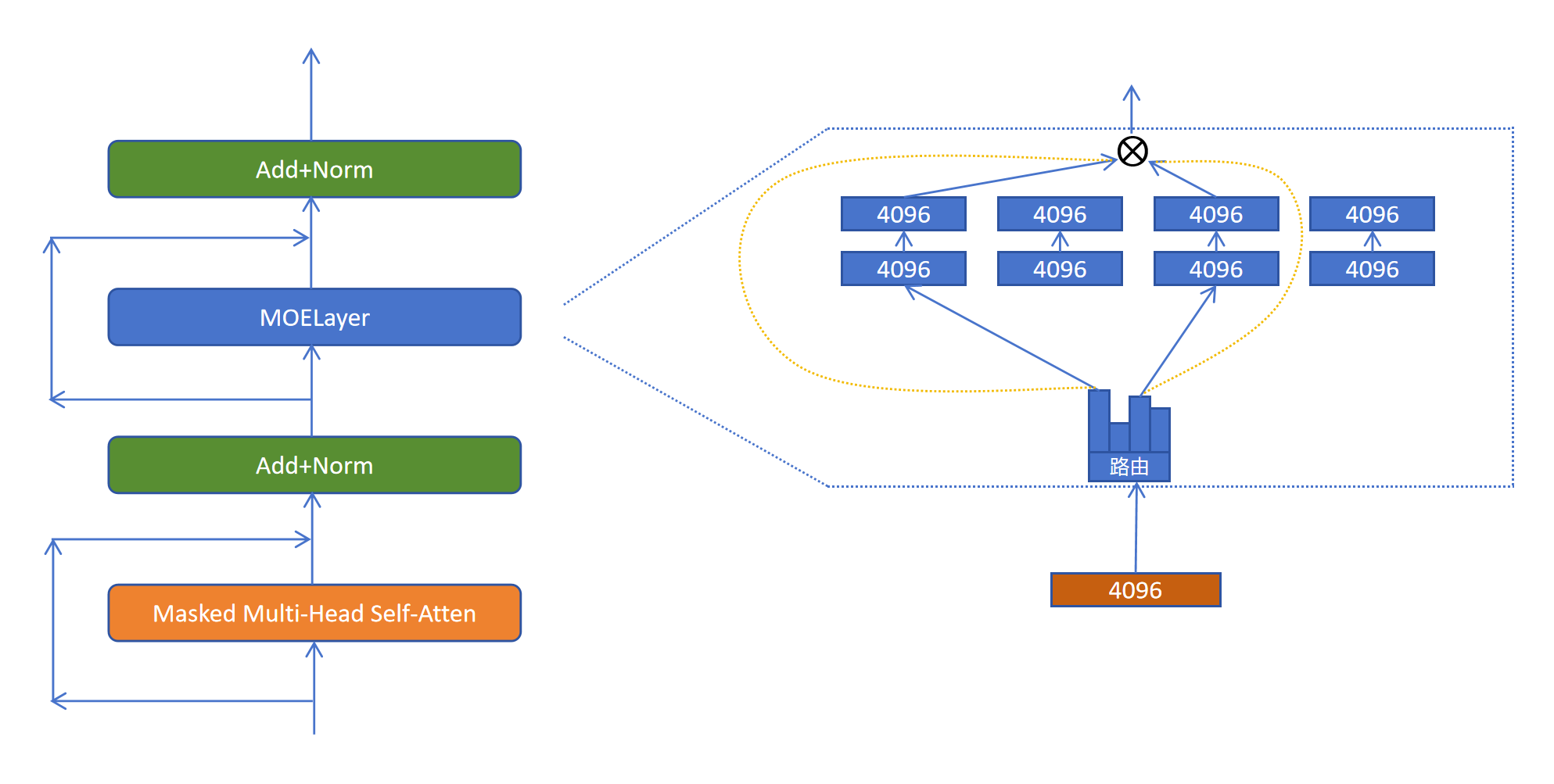
MOELayer将原来的一个全连接模块，拆分为多个小的全连接模块。里边每个线性层的维度都是4096x4096。这些小的一个个的全连接模块就被称为是一个个专家网络。那对于每个token该选择走哪个专家呢？答案是通过路由网络来决定。路由网络输出每个token走每个专家网络的概率。然后找出其中概率值最大的几个专家，具体几个专家被选中，也是一个可以调节的超参数。比如上图中，选择排名靠前的前两名专家。然后让token的特征，通过选中的这两个专家网络，得到两个维度为4096的特征向量，然后这两个特征向量按照专家被选中的权重值进行加权求和，就得到了MOELayer对于这个token的最终输出。这里需要注意的是专家的选择是对每个token进行的，不是对当前序列的。

18.1.2 MOE架构的特点

因为MOELayer减少了计算量，所以在相同的计算代价下，MOE模型可以增大网络参数的规模，性能更好。基本可以达到和相同参数规模的稠密模型的网络性能。

相比同等参数规模的稠密网络，MOE模型计算代价变小，但是显存占用不变。因为所有的专家网络都是要被加载到显存中。

MOE模型的训练难度比稠密模型要大，因为可能存在专家负载不均衡的问题，造成大量的token都被少数几个专家网络处理的情况，其他的专家网络占用了网络参数，但是却很难被激活。

18.1.3 专家负载均衡

为了让专家负载均衡，人们想了很多办法。

训练时，每个token最少选择2个专家，选择概率最大的专家，然后在剩下的专家里按概率再选择一个专家进行训练。这样防止专家概率低，得不到训练，得不到训练，性能差，性能差被选择概率更小的恶性循环。

还有一种做法是给每个专家设置token容量，也就是在一个batch里每个专家能处理的最大token数。当每个专家处理的token到达容量限制后，则跳过对这个token的处理。这些被跳过的 token 在本层就不经过专家计算，直接通过残差连接带到下一层。

还有一种做法就是设置一个负载均衡的辅助损失。让模型在训练过程中自己学会负载均衡。

18.1.4 负载均衡损失

负载均衡损失的目的就是希望每个专家被调用的频率是相等时损失最小。 第i个专家被调用的频率$f_i$就等于该专家被调用的次数除以所有专家被调用的次数。 loss函数定义为：

$Loss_{balance}=\sum_{i=1}^N(f_i)^2$

我们通过一个例子来理解这个loss函数。 假设有两个专家，如果是最极端的情况，分配最不平衡的情况，每个token都调用第一个专家。

$f_1=1;f_2=0; \qquad loss_{balance}=1^2+0^2=1$

稍微平衡一点的情况，第一个专家有0.8的概率被调用，第二个专家有0.2的概率被调用。

$f_1=0.8;f_2=0.2; \qquad loss_{balance}=0.8^2+0.2^2=0.68$

绝对平衡的情况，两个专家都各有0.5的概率被调用到：

$f_1=0.5;f_2=0.5; \qquad loss_{balance}=0.5^2+0.5^2=0.5$

如果要严格证明为这么只有负载均衡时，这个loss最小，可以通过柯西不等式来证明。我们这里就不做证明了。

然而这个损失函数却不能直接被拿来当做MOE网络的损失函数。因为我们计算每个专家被调用的次数，是通过torch.topk这样取前几个最大值的方式来获取的。这个操作并不是数值计算，不可微分，无法通过梯度下降算法来进行优化。

作为改进，我们定义负载均衡的损失函数为:

$loss_{balance}=\sum_{i=1}^N{f_ip_i}$

可以看到上式中将一个频率值$f_i$替换为概率值$p_i$。$p_i$的值是一个批次中所有token对该专家的路由概率的平均值。理论上这里的概率平均值当token无穷大时就等于这个专家被选择的频率值。这样做有个好处，这个概率值是通过softmax数据计算得来的，是可以微分的，可以通过梯度下降来进行优化改进让所有专家负载均衡。