10.3 卷积操作的进阶

上一节我们讲了一些卷积的基本操作，这一节我们继续来学习卷积操作。

10.3.1 感受野

对原始的图片连续做两次的3x3的卷积操作。

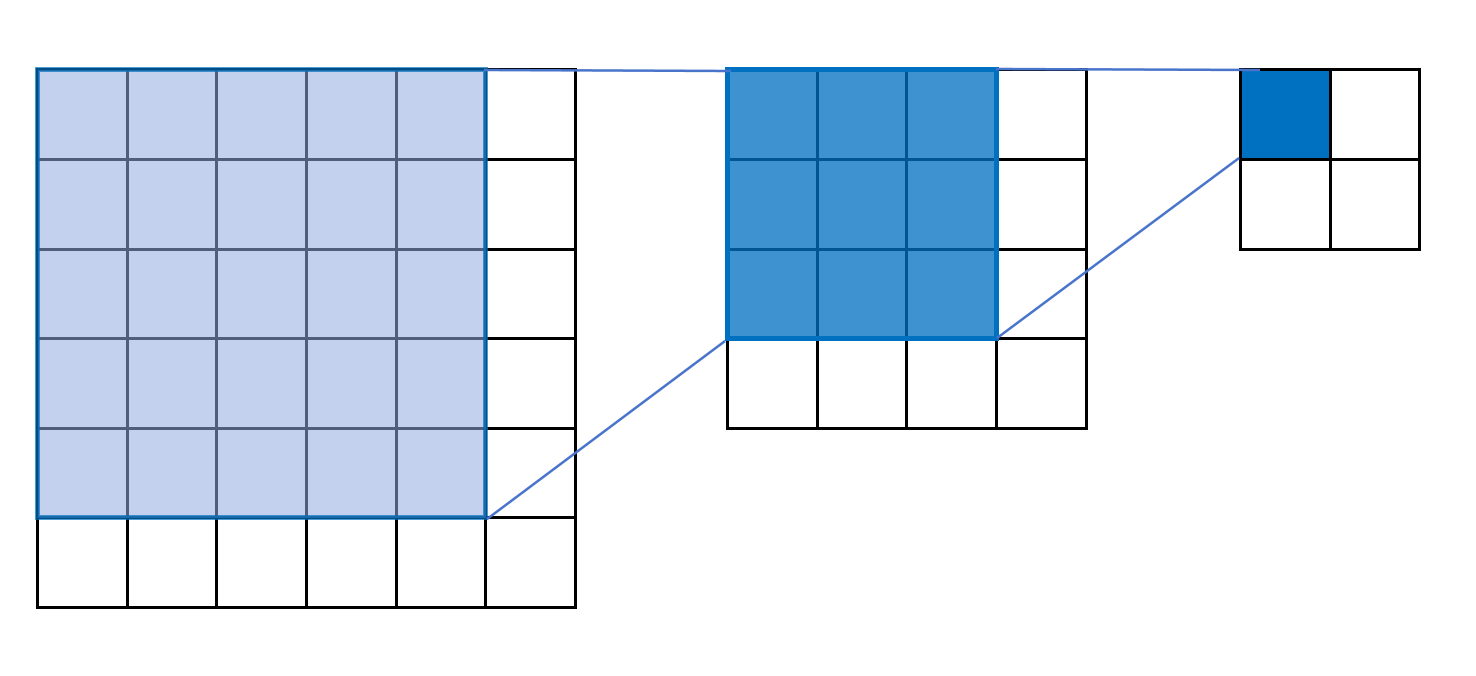
如果原始图片的尺寸为6x6，那么做完第一次3x3的卷积后，生成的特征图为4x4，在这4x4的特征图里，每个特征都是由原始图片里3x3的像素参与运算得到。所以我们说第一次卷积操作生成的特征图的感受野是3x3。

在第一次卷积生成的特征图上我们继续做第二次卷积，得到的特征图大小为2x2，在这个2x2的特征图里，每个特征都是由原始图片里5x5的像素参与运算得到的。所以我们说第二次卷积操作生成的特征图的感受野是5x5。

感受野是指当前特征图里的每个特征是由原始多大区域的像素参与运算得到的。

我们通过观察可以看到，随着卷积的不断进行，生成的特征图越来越小，但是特征图的感受野越来越大。这刚好也契合了深度神经网络的特性，浅层网络发现细节局部的特征，深层网络发现更加宏观整体的特征。

10.3.2 卷积核的大小

之前我们讲的卷积核的大小为3x3，当然你也可以设置其他大小，比如5x5,7x7等，但是一般我们都设为奇数的正方形。目前最常用的卷积核都是3x3的。这是因为奇数核具有唯一的中心像素，便于定位特征。例如，3×3核的中心是第2行第2列，这为卷积操作提供了对称的参考点，使特征提取更直观。

你不用担心3x3的卷积核能看到的像素太少，以至于发现不了什么有用的特征。上边我们通过分析特征图的感受野知道，经过几次3x3的卷积，后边特征图的感受野会不断增大的。

10.3.3 步长

步长（stride），之前我们讲卷积核在特征图上滑动，不论从左到右，还是从上到下都是一个像素一个像素的滑动，也就是步长为1。你也可以设置步长为其他值，比如2，那么卷积操作生成的特征图将更快的缩小。一般情况下，我们都设置步长为1，这样能提取更多细节特征。

如果你的卷积核设置比较大，比如7x7，证明你要检测的特征比较大，那么你可以对应的将步长设置为2。这样每次滑动后，滑过的区域相对于检测框来说不大，漏掉要检测的特征概率较小。 如果你的卷积核设置比较小，比如3x3，那么你要检测的特征也比较小，那么你最好把步长设置为1。如果设置为2的话，可能会漏掉你要检测的特征。

10.3.4 Padding

我们目前学到的卷积操作有两个问题：

1. 每次经过卷积操作，得到新的特征图会变小，在图片原本尺寸就很小的情况下，特征图经过几层就变的非常小，无法进行卷积操作了。我们希望有一种方法能保持特征图的尺寸，从而可以添加更多的卷积层，增加网络的深度。

2. 卷积操作，对于处于图片中央的像素，会被多次用于计算，而处于边缘的像素用于计算的次数则较少。 比如对于处于图片中央的像素，在3x3的卷积核下，会参与9次运算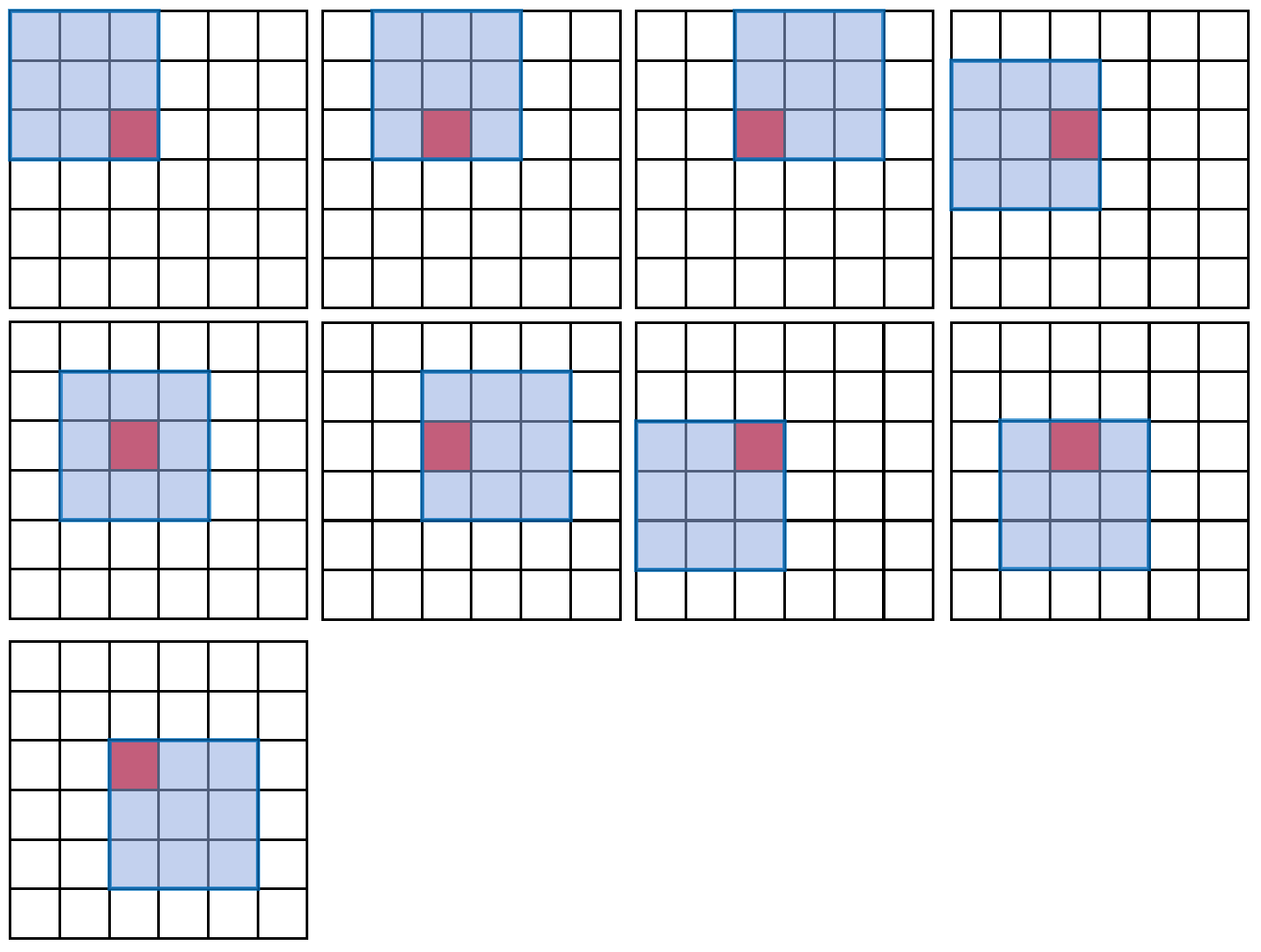： 但是，如果一个像素处于左上角，它只参与一次运算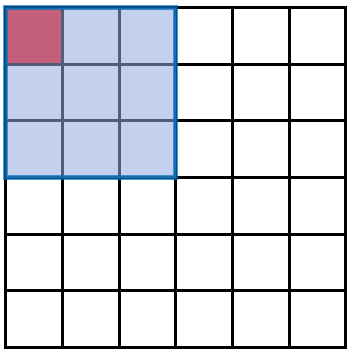： 为了解决上边的两个问题，人们引入了Padding操作。 Padding操作就是在图片周围添加全0的像素。相当于给原始图片周围加了一圈黑边。当然也有其他Padding的做法，比如有一种填充方法就是重复边缘的像素来进行填充。我们最常用的还是全零填充。

以0填充为例，Padding为1，就是在图像周围填充一圈0。Padding为2，就是在图像周围填充两圈0。

以6x6的原始图片输入，Padding为1，则Padding后的结果为： Size 为1的Padding后的6x6的图像变为了8x8。它解决了上边所说的两个问题，原始图片左上角的像素可以参与4次计算。另外在填充后8x8的图片上按照步长为1,3x3的卷积，生成的特征图，还是6x6。它保持了和原始实际图片同样的大小。如果我们还要接着进行卷积操作，同时还想保证特征图的尺寸不变，那么我们可以在生成的6x6的特征图上继续进行填充。

10.3.5 生成特征图的尺寸计算

在卷积神经网络里，特征图的尺寸主要取决于以下几个参数：

• 输入尺寸：$W_{in}$（宽度），$H_{in}$(高度）
• 卷积核尺寸：K
• 填充值：P
• 步长：S
• 输出尺寸：$W_{out}$（宽度），$H_{out}$(高度）

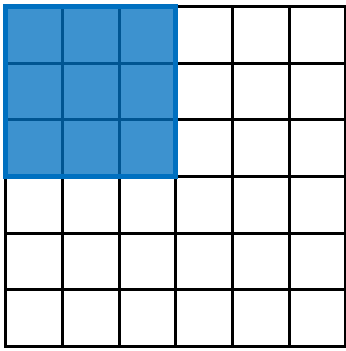比如对于上边特征图$W_{in}=H_{in}=6,K=3,P=0,S=1$。 对于$W_{out}$，如上图，卷积核目前占据了左上角的一个位置，它将产出一个输出特征。另外宽度方向，还剩余$W_{in}-K$个像素，每次移动一个像素，那就可以再在宽度方向产生$W_{in}-K$个输出。所以：

$W_{out}=1+W_{in}-K$

输出特征的数量 = 可以移动多少次 + 1。其中1是卷积核的初始位置产生的输出。

上边这个例子比较简单，没有考虑Padding，步长也为1，我们看一个复杂的情况。

比如对于上边特征图$W_{in}=H_{in}=6,K=3,P=1,S=2$。这次我们加入了Padding=1，步长为2。 我们发现，Padding为1，实际图片宽度增加了2。也就是Padding后的图片宽度为$W_{in}+2P$。 还和上次一样，除了目前图上卷积核所在的位置产出一个特征外，宽度方向剩余了$W_{in}+2P-K$个像素。然后除以步长S，就是还可以产生的输出特征。 所以：

$W_{out}=1+\frac{W_{in}+2P-K}{S}$

最后还有一点需要注意，就是这个除法可能除不尽。比如对于步长为2的情况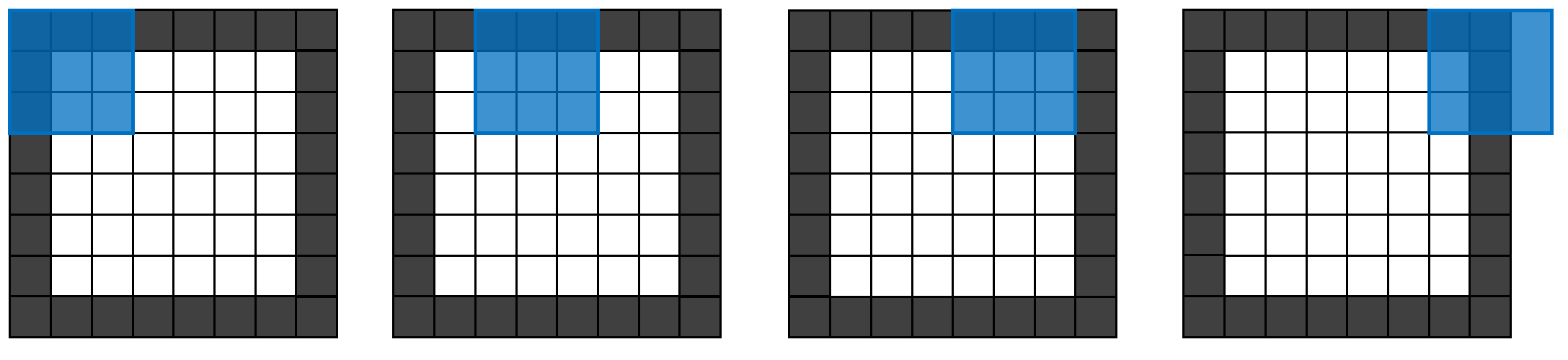： 除不尽的情况就对应于第四部，卷积核有一部分落在特征图外边的情况。默认做法是舍弃这一步。对应到计算公式上，就是对除法向下取整。所以我们得到最终的公式为：

$W_{out}=1+\left \lfloor \frac{W_{in}+2P-K}{S} \right \rfloor$

对于高度的公式同样为：

$H_{out}=1+\left \lfloor \frac{H_{in}+2P-K}{S} \right \rfloor$

另外我们来计算一下如果S=1，想要让输出特征图保持和输入特征图一致。也就是$W_{out}=W_{in}$，那么P应该等于多少呢？

$W_{in}=1+W_{in}+2P-K$

得到，填充值应该为：

$P=\frac{K-1}{2}$

为了让填充值为整数，所以卷积核大小K应该为奇数。