4.2 概率里的基本计算

你可能之前学到过一些和概率计算相关的知识，我们来快速复习一下。

4.2.1 乘法原理

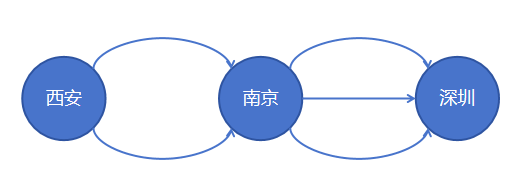
假如你要从西安经由南京去深圳。从西安到南京有2个航班可以选择，从南京到深圳有3个航班可以选择。那么你的行程有几种可能？如果你完全平等的选择每个航段的航班，那么每种行程的概率为多大？

完成这件事分为两步，第一步有两种可能的选择，第二步有三种可能的选择，所以一共有$2\times 3=6$种不同的可能，如果每种可能性的概率相等，那么每种可能的概率就为$\frac{1}{6}$

更正式的定义为：

如果一件事需要经过n步完成，每一步有k种方法完成，第i步有$k_i$种方法完成，则整件事有：

种方法完成。

4.2.2 加法原理

你投一个骰子，得到小于3点的概率为多大？

小于3点就只有2点和1点。1点的概率为$\frac{1}{6}$，2点的概率为$\frac{1}{6}$，所以小于3点的概率就为：

这就是加法原理，更正式的定义为：

如果一件事有n种方案完成，每种方案又有k种不同的实现方法，第i个方案有$k_i$种方法实现，则整件事有：

种方法完成。

4.2.3 排列

如果小明，小刚，小强站成一排，一共有多少种不同的排法？

第一个位置三个人都可以选，有三种可能。第一个人确定后，第二个位置有2个人可以选，有2种可能。前两个人确定后，最后一个位置只剩一个人，只有一种可能。

按照乘法原理，一共有：

种可能。

假如有4个人，选两个人出来排队，一共有几种排法？

同理，第一个位置有4种可能，第一个位置人确定后，第二个位置有3种可能。

按照乘法原理一共有：

种可能。

更正式的定义如下：

从n个不同元素里取r个元素进行排列，不能重复选择元素，并且考虑元素的位置顺序。则这是一个排列问题。按照乘法原理，这种排列共有：

记作$P_n^r$

如果当r=n时，称为一个全排列。此时也可以记作$P_n$，且$P_n=n!$

4.2.4 组合

有4个同学，你从中选出2个人来，有几种不同的可能？

这是一个组合问题，组合问题和排列问题不同的是，不需要考虑顺序。

但分析过程我们可以先考虑顺序，如果考虑顺序，四个人里选两个的答案为：

因为我们考虑了顺序，选出来的两个人里不同的排列顺序为：

最终我们用除法去除掉排列顺序的影响，所以做种答案为：

我们给出正式的定义：

从n个元素中选取r个元素作为一组，不考虑顺序，则这是一个组合问题。可能的组合数为：