3.8方向导数与梯度

3.8.1 方向导数

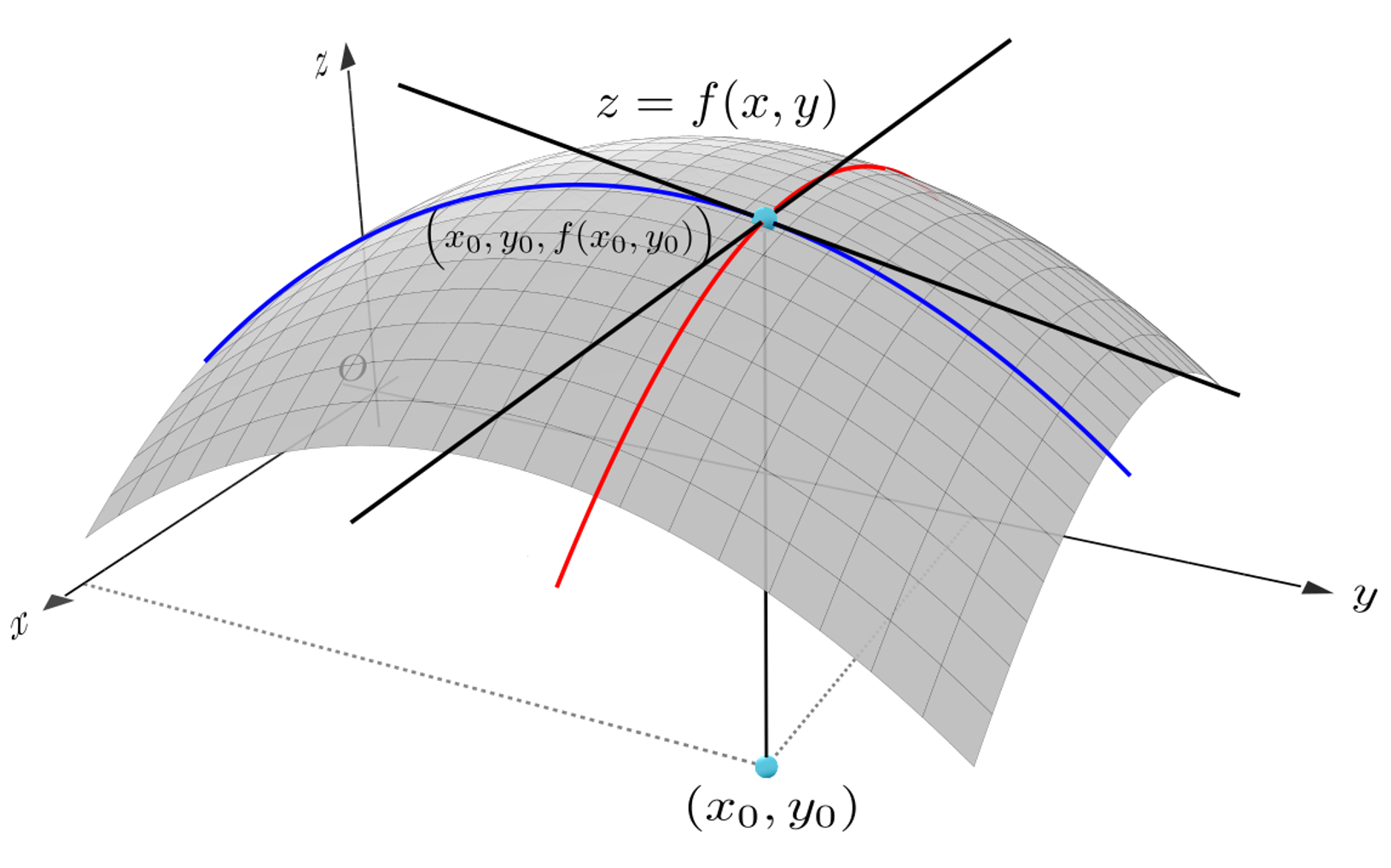
之前我们学过偏导数，我们再来回忆一下，函数$z=f(x,y)$在$(x_0,y_0)$点可以分别对x和y求偏导。对x求偏导时，保持y不变，$y=y_0$，只考虑x变化时，对z的影响。对y求偏导时，保持x不变，$x=x_0$，只考虑y变化时，对z的影响。

但现实情况是自变量在点$(x_0,y_0)$处不光可以沿着平行于x轴（x的偏导），或者沿着平行于y轴（y的偏导）变化，它是可以沿着各个方向进行运动变化的，我们想要研究当自变量沿着不同方向进行变化时，因变量的变化率，这就是方向导数需要研究的内容。

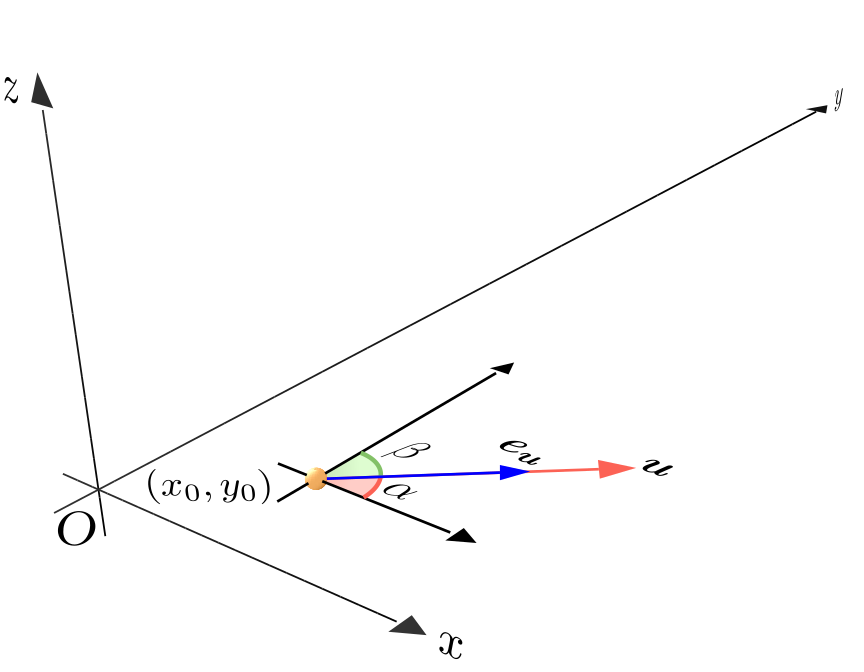
在$(x_0,y_0)$点用一个单位方向向量$e_u$来表示自变量变化的方向，因为$e_u$的模长为1，它与x轴夹角为α，与y轴夹角为β。以$(x_0,y_0)$作为新坐标系的原点，可以用向量[cosα,cosβ]来表示这个单位方向向量。

下边我们给出函数$z=f(x,y)$在$(x_0,y_0)$点，沿单位方向向量$e_u$的方向导数的定义：

上边极限表达式的分子部分是$\triangle z$,然后根据我们上一小节全微分的定义:

$\triangle z=f_x(x_0,y_0)\triangle x+f_y(x_0,y_0)\triangle y+O(\sqrt {(\triangle x)^2+(\triangle y)^2});(\sqrt {(\triangle x)^2+(\triangle y)^2} \to 0)$

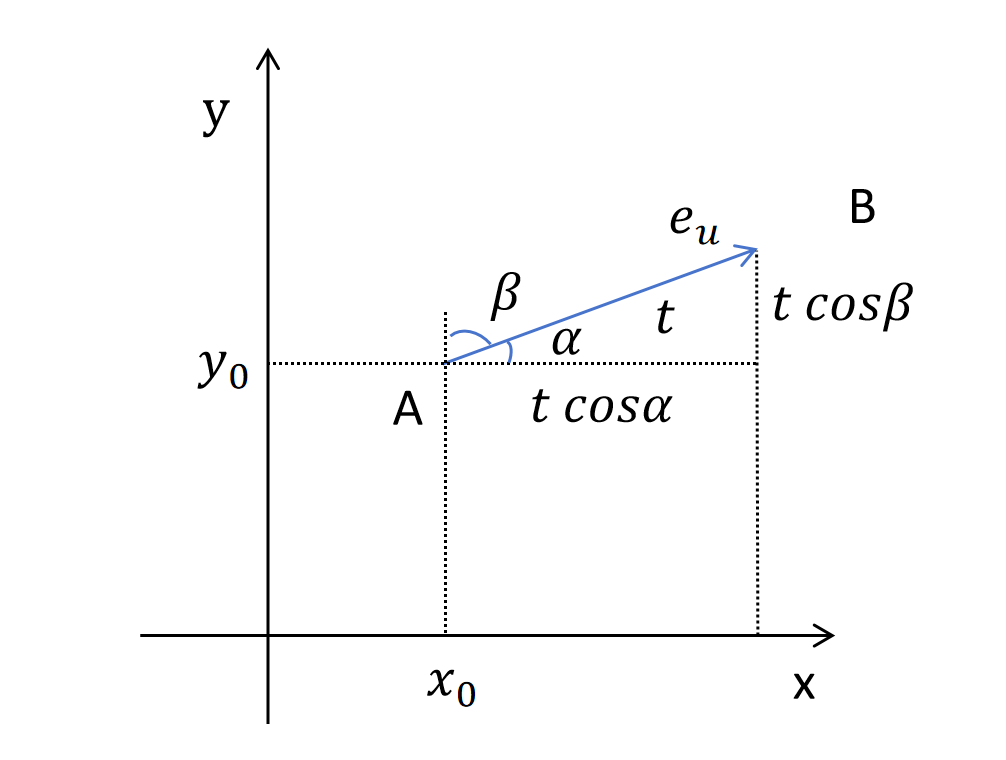
其中$\sqrt {(\triangle x)^2+(\triangle y)^2}$就表示A点和B点之间的距离t，$\triangle x=t \cos \alpha,\triangle y=t \cos \beta$ 所以上式可以转化为：

我们将$\triangle z$的表达式替换到方向导数的极限表达式3-4的分子部分,有：

最终可以得到函数$z=f(x,y)$在$(x_0,y_0)$点，沿单位方向向量$e_u$的方向导数为：

这个式子可以看做是向量$[f_x(x_0,y_0),f_y(x_0,y_0)]$和向量$[\cos \alpha,\cos \beta]$的点乘。

3.8.2 梯度

方向导数研究的是自变量沿着不同方向变化时，因变量的变化率。那么我们自然就关心自变量沿着哪个方向变化，因变量增加最快。根据上边对方向导数的推导，方向导数的值等于方向向量与函数对不同自变量求偏导形成的向量之间的点乘。我们之前介绍过向量点乘的结果是个标量，它的值就等于两个向量的模长乘以它们之间夹角的cos值。方向向量的模长为1，偏导数向量的模长固定，那么能改动的就是这两个向量之间的夹角了，只有让两个向量之间的夹角为0，cos值为1，可以让方向导数取到最大值。也就是让单位方向向量的方向与偏导数向量的方向一致，这时函数变化率最大。

看来用函数在某点，不同维度偏导数作为向量元素，构成的偏导数向量是个特殊的向量，沿着它的方向，可以让函数在此点变化率最大。我们就把这个向量叫做梯度。

如果有一个函数$f(x_1,x_2,...,x_n)$,它的梯度记作$\nabla f$或者grad $f$,表示为：

其中$f_{x_i}$是f关于$x_i$的偏导数。

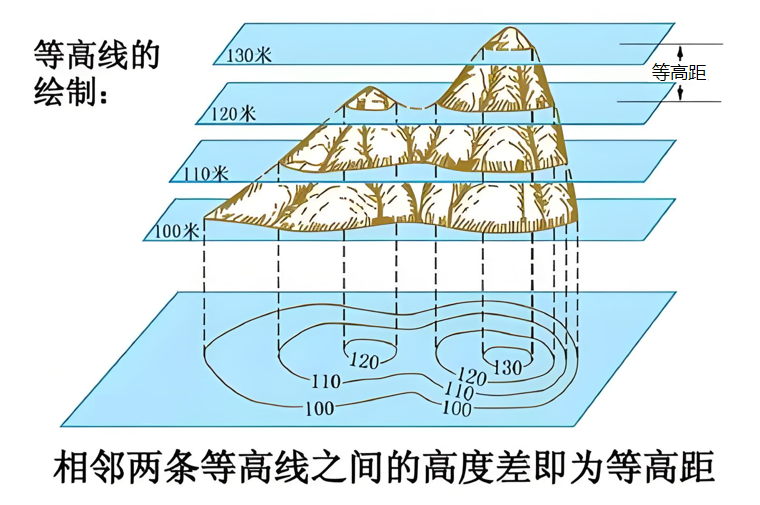
3.8.3 等高线

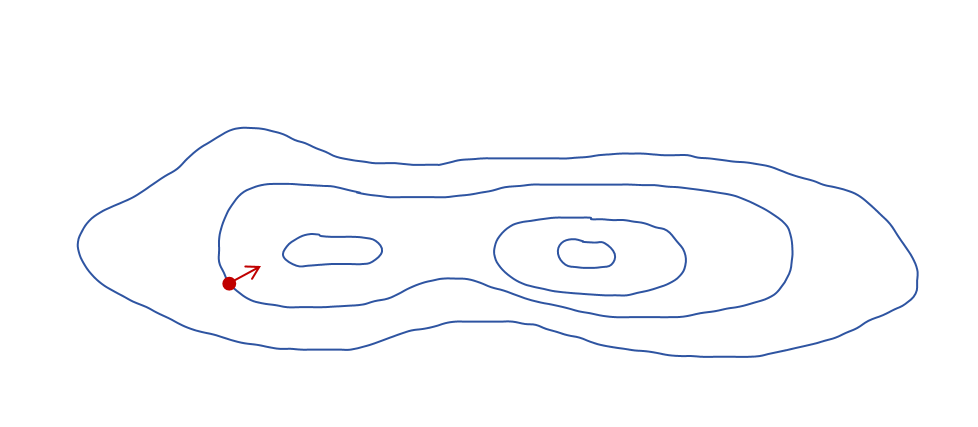
等高线是地形图上一种用来表示相同海拔点连成的曲线。它通过将具有相同高度的地面点连接在一起，展示地形的高低起伏和地势形态。从而可以用二维图展示三维信息。

如果用等高线来表示一个函数z=f(x,y)。x,y 坐标轴构成水平面，z轴表示高度。则在某一点$(x_0,y_0)$上的梯度方向，就垂直于该点所在的等高线，并指向函数值增高的方向。因为这个方向就是在该点让函数值增加最快的方向。

3.8.4 深度学习中的梯度

梯度在深度学习中起着至关重要的作用，是优化和训练过程中的核心工具。深度学习的本质是通过不断调整模型的参数，使其在输入数据上表现得更好，而实现这一目标的关键方法就是利用梯度信息。

梯度是损失函数（通常用来衡量模型预测值和真实值之间的差异）对模型参数的偏导数。它提供了两个重要的信息：

1. 方向：梯度的方向指向使损失函数值增长最快的方向，沿着负梯度方向移动，则可以使损失函数值最快的减少。
2. 速率：梯度的模长反映了参数变化对损失函数变化的影响程度，模长越大，参数的变化对损失的影响越大。

在深度学习训练过程中，模型利用梯度来指导参数更新，这一过程被称为优化。通过计算损失函数相对于模型参数的梯度，优化算法可以确定如何调整参数，使得模型的损失逐步减小，从而提高模型的性能。