4.8 中心极限定理和正态分布

4.8.1 正态分布

首先我们看一下高尔顿钉板。

很多钢珠从钉板上方中间下落，经过钉板上的钉子的阻挡，随机弹开，最终落下到一个个竖槽里。结果形成一个钟形曲线。这个曲线就是正态分布的曲线。正态分布的英文是Normal Distribution，可能翻译为常态分布更合适。为什么它是常态分布呢？因为在自然界和人类社会里，这种分布实在太常见了。 下边这些随机变量都符合正态分布：

• 人的身高
• 高考成绩
• 一批产品每个的重量
• 深度学习里模型的误差
  

正态分布也叫高斯分布，因为他在研究天文学中的测量误差时首次系统地研究了这种分布。正态分布在科研工作中非常有用，以至于为了纪念高斯和他发现的正态分布，曾经将正态分布印在了德国10马克钱币上。

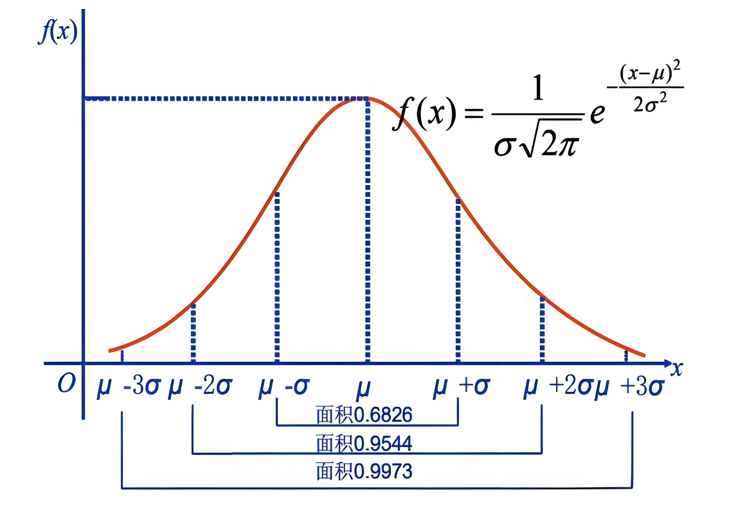
正态分布的概率密度函数如上图所示。符合正态分布的随机变量的结果有68%的概率分布在距离均值左右一倍标准差的范围内，95%的概率分布在距离均值左右2倍标准差的范围内，99.7%的概率分布在距离均值左右3倍标准差范围内。

4.8.2 中心极限定理

为什么自然界中有如此多的正态分布呢？那就不得不提到中心极限定理。

首先我们先大致分析一下为什么从高尔顿钉板落下的钢珠符合正态分布，也就是最终落到中间格子的钢珠多，落到两边的钢珠少。

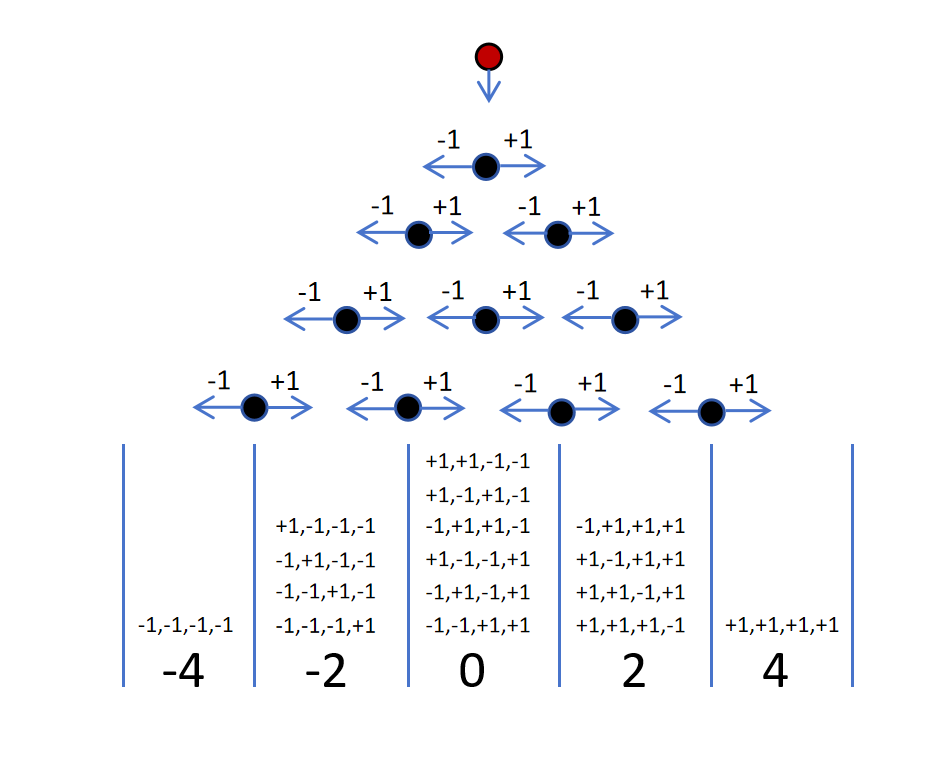
假设钉板有4层，每个钢珠碰到每个钉子有0.5的概率向左，记作-1，有0.5的概率向右，记作+1，则落入最右侧格子的情况只有一种，就是碰到每一个钉子都向右加1，最终结果为4。只有一种排列情况。

落入最左边格子情况类似，只有一种排列情况。落入左二和右二都有4种排列情况。落入中间的排列情况最多，有6种情况。

因此，导致高尔顿钉板最终钢珠落下形成的分布为中间高，两边低的正态分布。

概括一下来说，钢珠一共会碰到4次钉子，每次的结果，向左或者向右是独立的，且他们都是同分布的(0.5左，0.5右）。随机变量X将左映射为-1，右映射为1。则最终四次实验的样本和$X_1+X_2+X_3+X_4$服从正态分布。同样，它们的均值也服从正态分布。

上边的表述已经很接近中心极限定理了。但还需要进行一些拓展，我们上边的随机实验里，钢珠碰到每个钉子，向左和向右的概率是相等的，是一个均匀分布。多个均匀分布的和才能产生正态分布吗？

我们进行下边的实验看看。

中心极限定理在线实验

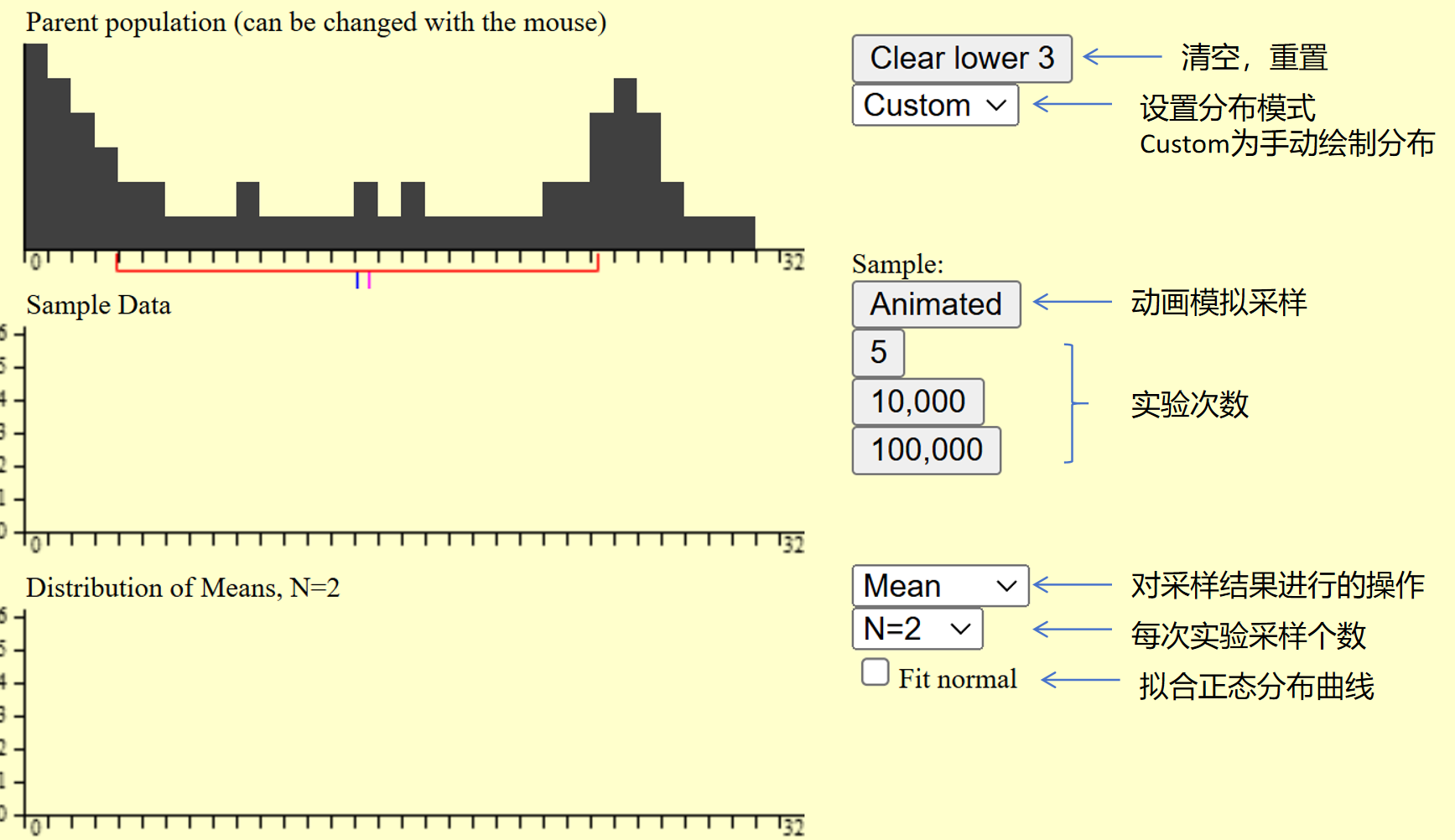
程序的配置项如上图所示。

我们先选择手动绘制一个非常不规则的分布，然后每次实验采样2个样本，计算这两个样本的均值，看看这些均值服从什么分布。我们实验10万次，并绘制由每次实验2个样本产生的均值的分布。

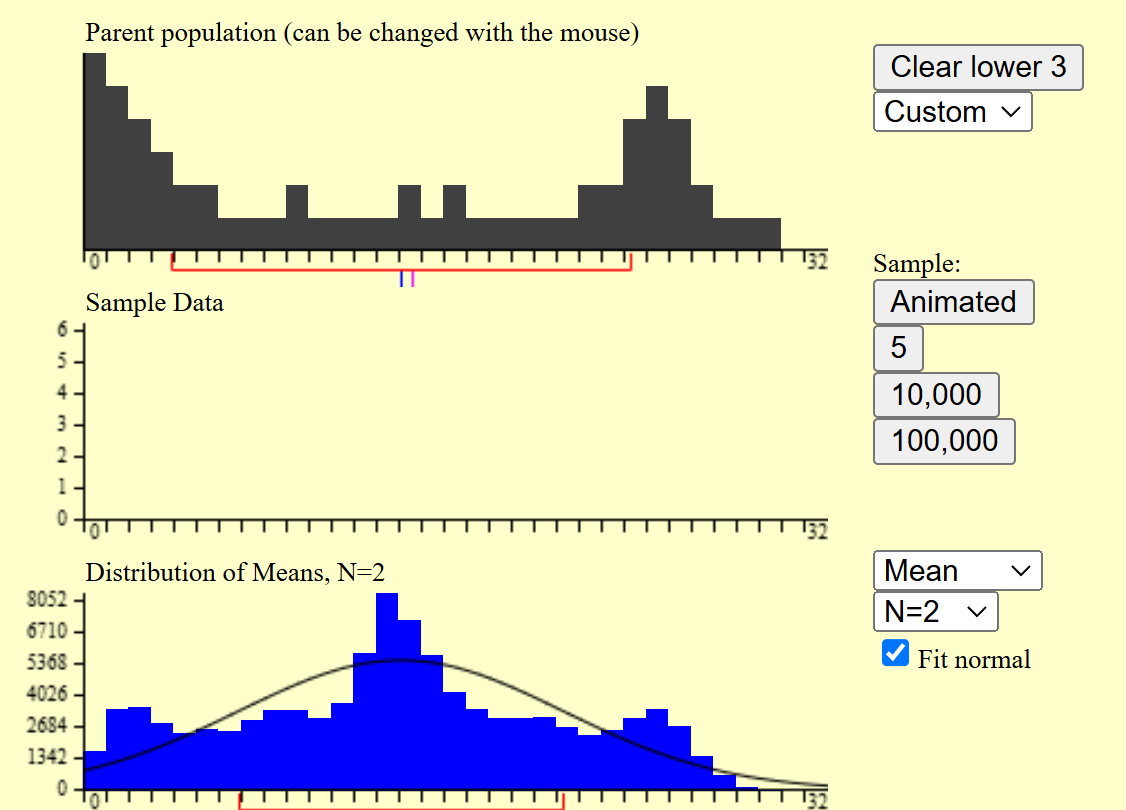
可以看到，虽然均值的分布中间高，两边低，但是仍不是一个完美的正态分布，我们可以提高每次实验采样的次数，从2提升到5。

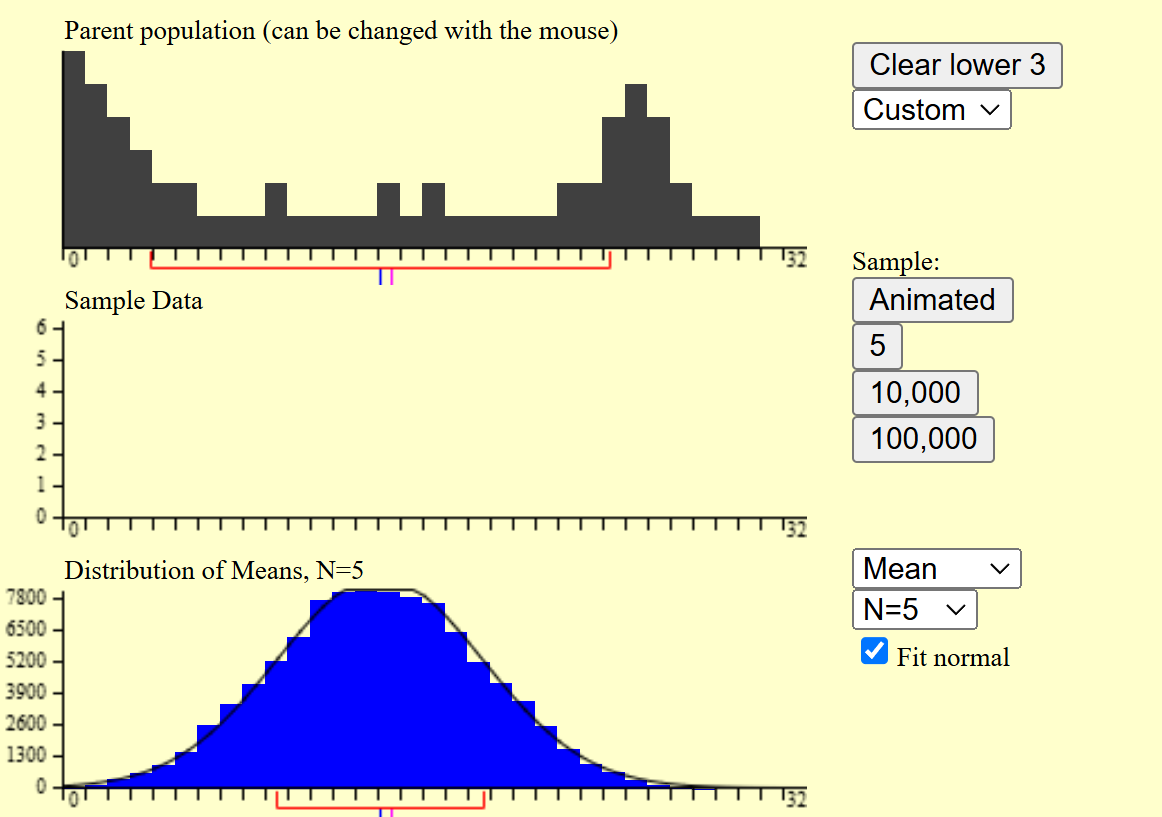
改进了不少，我们继续讲每次采样的次数提升到20。

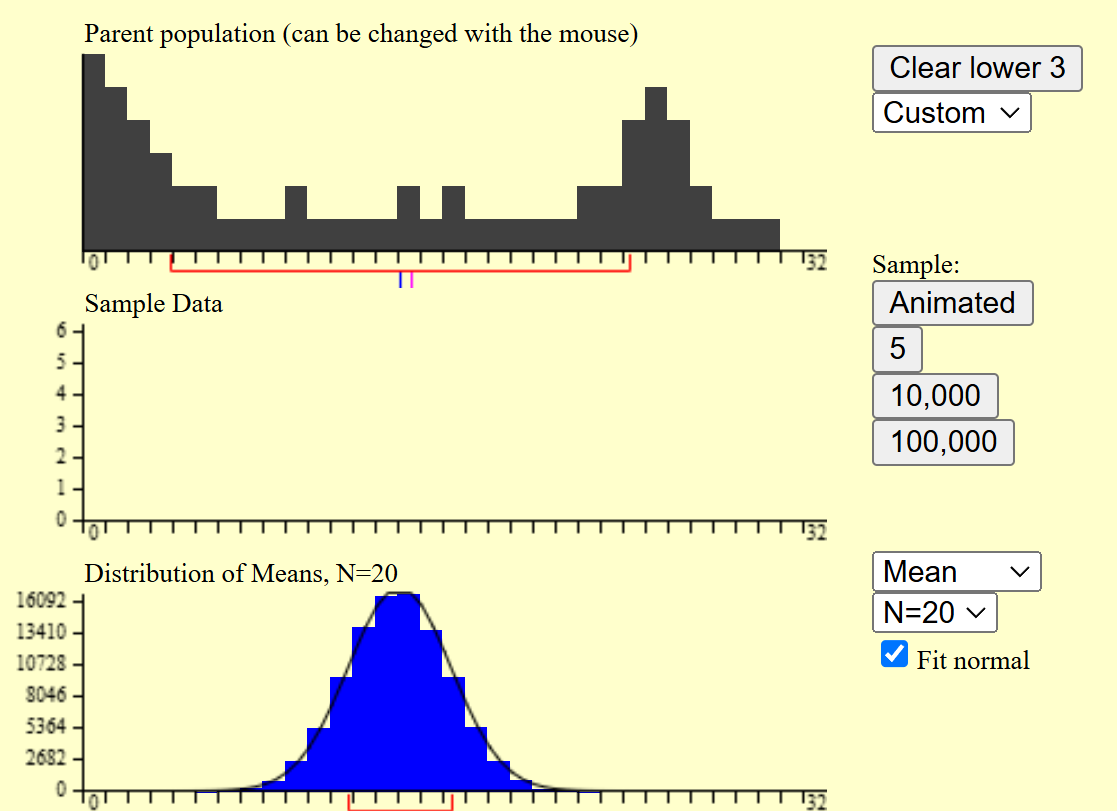
这次我们得到了一个完美的正态分布曲线。

通过这个实验，我们可以得到两点启示。

• 不论原始分布是怎样的，每次实验对原始分布进行采样，然后计算这些样本的均值。进行多次实验，这些均值服从正态分布。
• 每次对原始分布采样次数要足够大，一般为20，才符合正态分布。

下边给出中心极限定理的定义：

无论单个随机变量的原始分布是什么样的，只要随机变量是独立同分布的，且具有有限的均值和方差，那么这些随机变量的和（或均值）在样本量足够大的情况下，其分布将趋近于正态分布。

4.8.3 中心极限定理的拓展

上边我们说的是严格的中心极限定理，拓展的中心极限定理，不要求所有的随机变量都是同分布的，只要这些随机变量是独立的，且具有有限的均值方差，没有占主导因素的随机变量，在样本量足够大的情况下，这些随机变量的和或者均值构成的分布也趋于正态分布。

根据对中心极限定理的拓展，就解释了自然界里为什么那么多现象都符合正态分布了，比如人的身高，是由大量随机因素共同决定的，所以符合正态分布。