2.3 线性变换和矩阵

线性代数里主要研究的是向量，以及对向量的操作。并且对于向量来说，基本操作就只有两个：数乘和向量加法。今天我们来学习对向量进行线性变换和矩阵。

2.3.1 线性变换

你可以将线性变换理解成对向量的一个函数，输入是一个向量，输出还是一个向量。但是这个函数必须满足对数乘和向量加法的封闭性：

加法封闭性：对于任意两个向量u和v，线性变换T满足:

T(u+v)=T(u)+T(v) T(u+v)=T(u)+T(v)

数乘封闭性：对于任意向量v和标量c，线性变换T满足：

T(cv)=cT(v) T(cv)=cT(v)

为什么线性变换必须满足加法封闭性和数乘封闭性呢？

首先因为向量的基本操作就两个：一个是数乘，一个是向量加法。

如果映射前向量a,b,c,d有以下关系：

c=a+b c=a+b

c=0.4d c=0.4d

a,b,c,d经过一个线性变换后，得到a',b',c',d'。我们希望以下关系还成立：

c′=a′+b′ {c}'={a}'+{b}'

c′=0.4d′ {c}'=0.4{d}'

加法封闭性和数乘封闭性就保证了这样性质的成立。保证了线性变换后向量之间的关系不发生变化。线性变换有两个非常好的性质：

直线保持：线性变换前多个终点在一条线上的向量，经过线性变换后，这些向量的终点仍在一条直线上。

原点不变：线性变换后原点仍然在原点位置。

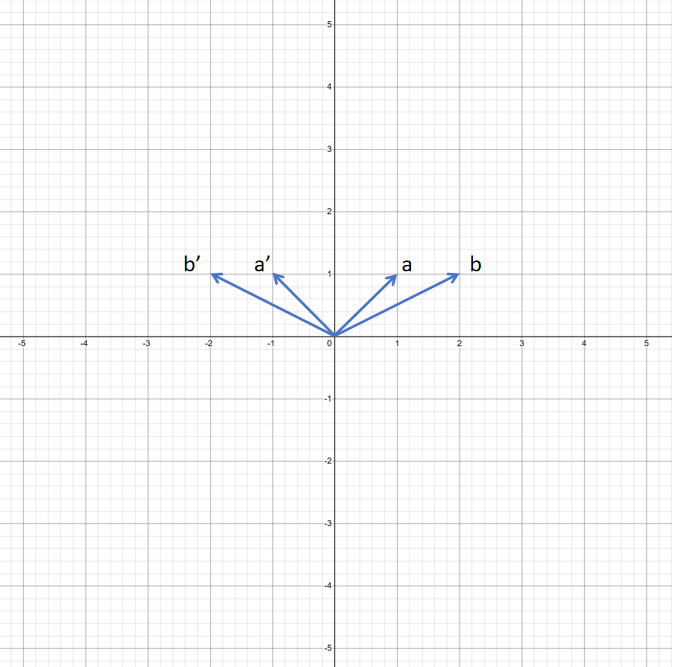
0208.png

通过线性变换，可以把一个向量进行拉伸，旋转，翻转等。那如何用数字准确表述这种线性变换呢？比如上图中向量a,b经过线性变换为a',b',线性变换的规则是对于二维空间的向量，x坐标取负值，y坐标不变，也就是沿y轴镜像。我们需要一个数学的方式来描述这个线性变换。

线性变换的表示 之前我们讲过一个向量和基的关系，我们再来复习一下。一个向量可以理解为用它的各个分量对标准基里的对应向量进行缩放，再将缩放后的基向量相加。

我们只需要记录标准基里的向量(i,j)经过线性变换后的向量(i',j')。原始向量各个分量对变换后的基向量的线性组合就是对该向量的线性变换后的向量。我们举一个例子：

还是以上图沿y轴镜像的线性变换的例子来说，用这个变换规则来对二维向量空间的标准基向量 i 和 j 进行变换。

i′=[−10]j′=[01] \mathbf{i'} =\begin{bmatrix}-1 \\0 \end{bmatrix}\mathbf{j'} =\begin{bmatrix}0 \\1\end{bmatrix}

原始向量b为：

b=[21] \mathbf{b} =\begin{bmatrix}2 \\1 \end{bmatrix}

对b进行相同线性变换时，只需要用b的各个分量对 i' 和 j' 进行缩放再相加就可以。

b′=2i′+1j′=2[−10]+1[01]=[−21] \mathbf{b'} =2i'+1j'=2\begin{bmatrix}-1 \\0 \end{bmatrix} + 1\begin{bmatrix}0 \\1 \end{bmatrix} = \begin{bmatrix}-2 \\1 \end{bmatrix}

也就是说只需要记录标准基经过线性变换后的基就可以表示这个线性变换了。

2.3.2 矩阵

每一个线性变换都可以对应一个矩阵，矩阵就是对向量进行线性变换的函数。矩阵就是由经过线性变换的标准基构成的。还是上边以y轴为镜像的例子，我们把线性变换后的 i' 和 j' 放在一起就构成了一个矩阵AA。

A=[−1001] A=\begin{bmatrix} -1&0 \\ 0&1 \end{bmatrix}

这个矩阵就表示对一个向量按Y轴进行镜像的线性转换。它对向量b的计算法则如下：

b=[21] b=\begin{bmatrix} 2\\ 1 \end{bmatrix}

Ab=2[−10]+1[01]=[−21] Ab=2\begin{bmatrix}-1 \\0 \end{bmatrix} + 1\begin{bmatrix}0 \\1 \end{bmatrix} = \begin{bmatrix}-2 \\1 \end{bmatrix}

我们可以再定义逆时针旋转90°的线性变换来试一下。

i′=[01]j′=[−10] \mathbf{i'} =\begin{bmatrix}0 \\1 \end{bmatrix}\mathbf{j'} =\begin{bmatrix}-1 \\0\end{bmatrix}

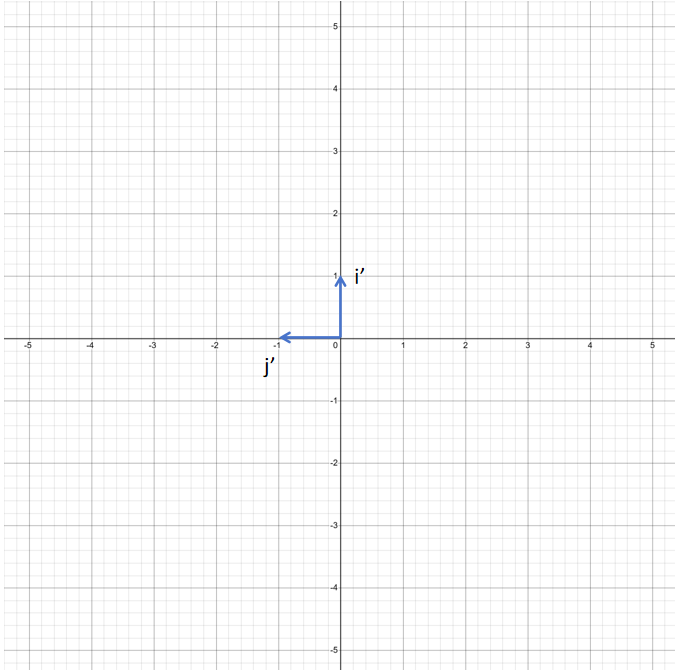
0209.png

接下来我们用 i' 和 j' 构成矩阵AA：

A=[0−110] A=\begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}

我们尝试对向量a进行线性变换，看是否可以对向量a逆时针旋转90°。

b=[21] \mathbf{b} =\begin{bmatrix}2 \\1 \end{bmatrix}

b′=Ab=[0−110][21]=2[01]+1[−10]=[−12] \mathbf{b'} =Ab=\begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}\begin{bmatrix}2 \\1 \end{bmatrix}=2\begin{bmatrix}0 \\1 \end{bmatrix} + 1\begin{bmatrix}-1 \\0 \end{bmatrix} = \begin{bmatrix}-1 \\2 \end{bmatrix}

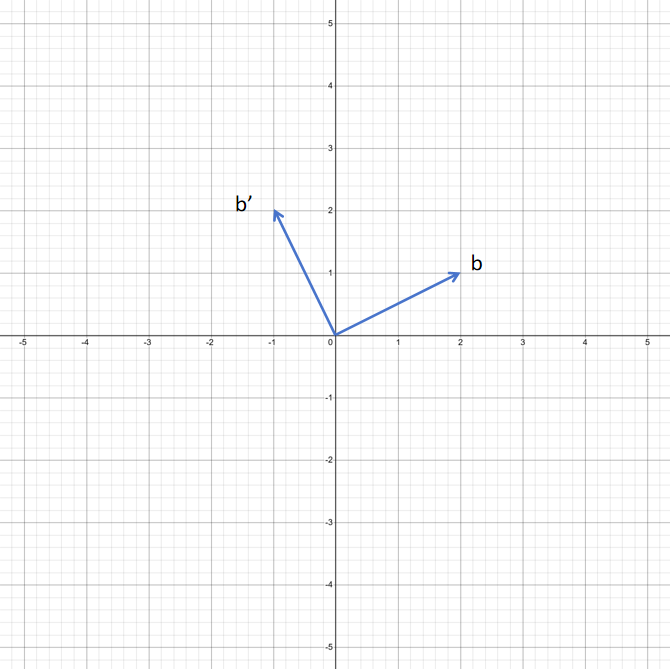
0210.png

可以看到矩阵AA确实可以对向量b进行逆时针旋转90°的线性变换。

单位矩阵

标准基向量构成的矩阵就是一个单位矩阵，单位矩阵对向量进行线性变换后还是向量本身。单位矩阵里的行数和列数相等，只有对角线上元素为1，其他位置元素为0。比如3维单位矩阵为：

I=[100010001] I=\begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix}

矩阵的行和列 上边我们讲的矩阵的行数和列数都是相等的，它们叫做方阵。但矩阵的行数和列数可以不相等。比如下边这个矩阵CC，它就是一个3行2列的矩阵。

C=[0−11021] C=\begin{bmatrix} 0&-1 \\ 1&0 \\ 2&1 \end{bmatrix}

矩阵CC也代表一个线性变换，矩阵CC里的第一列是把二维向量空间里的 i 向量通过这个线性变换得到的3维向量。矩阵CC里的第二列是把二维向量空间里的 j 向量通过这个线性变换得到的3维向量。所以矩阵CC是一个可以把2维向量映射到3维向量的线性变换。矩阵CC对于向量b进行向量变换如下：

b=[21] \mathbf{b} =\begin{bmatrix}2 \\1 \end{bmatrix}

b′=Cb=[0−11021][21]=2[012]+1[−101]=[−125] \mathbf{b'} =Cb=\begin{bmatrix} 0&-1 \\ 1&0 \\ 2&1 \end{bmatrix}\begin{bmatrix}2 \\1 \end{bmatrix}=2\begin{bmatrix}0 \\1\\2 \end{bmatrix} + 1\begin{bmatrix}-1 \\0 \\1\end{bmatrix} = \begin{bmatrix}-1 \\2\\5 \end{bmatrix}

所以，不是方阵的矩阵进行的线性变换，会给进行变换的向量带来维度上的变换。上边的例子，是把一个2维向量变换为3维向量。下边我们看一个把3维向量变换为2维向量的例子。比如下边矩阵DD，它是一个2行3列的矩阵，它就可以把3维向量线性变换为2维向量。

D=[0−11102] D=\begin{bmatrix} 0&-1&1 \\ 1&0&2 \end{bmatrix}

c=[211] \mathbf{c} =\begin{bmatrix}2 \\1\\1 \end{bmatrix}

c′=Dc=[0−11102][211]=2[01]+1[−10]+1[12]=[04] \mathbf{c'} =Dc=\begin{bmatrix} 0&-1&1 \\ 1&0&2 \end{bmatrix}\begin{bmatrix}2 \\1\\1\end{bmatrix}=2\begin{bmatrix}0 \\1 \end{bmatrix} + 1\begin{bmatrix}-1 \\0\end{bmatrix} + 1\begin{bmatrix}1 \\2\end{bmatrix}= \begin{bmatrix}0 \\4 \end{bmatrix}

矩阵乘法

比如代表逆时针旋转90°的矩阵AA,可以同时对3个向量进行旋转。

A=[0−110] A=\begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}

a=[01]b=[11]c=[−11] \mathbf{a} =\begin{bmatrix}0 \\1 \end{bmatrix}\mathbf{b} =\begin{bmatrix}1 \\1 \end{bmatrix}\mathbf{c} =\begin{bmatrix}-1 \\1 \end{bmatrix}

可以把a,b,c组成一个矩阵BB：

B=[01−1111] B=\begin{bmatrix} 0&1&-1 \\ 1&1&1 \end{bmatrix}

AB=[0−110][01−1111] AB=\begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}\begin{bmatrix} 0&1&-1 \\ 1&1&1 \end{bmatrix}

这就变成了矩阵之间的乘法，它的计算法则就是先取BB矩阵的第一列，用AA进行线性变换。

[0−110][01]=[−10] \begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}\begin{bmatrix}0 \\1 \end{bmatrix}=\begin{bmatrix}-1 \\0 \end{bmatrix}

然后取BB矩阵的第二列，用AA进行线性变换。

[0−110][11]=[−11] \begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}\begin{bmatrix}1 \\1 \end{bmatrix}=\begin{bmatrix}-1 \\1 \end{bmatrix}

最后取BB矩阵的第三列，用AA进行线性变换。

[0−110][−11]=[−1−1] \begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}\begin{bmatrix}-1 \\1 \end{bmatrix}=\begin{bmatrix}-1 \\-1 \end{bmatrix}

最后把三个向量经过线性变换后的向量组成最终的结果矩阵：

[−1−1−101−1] \begin{bmatrix} -1&-1&-1 \\ 0&1&-1 \end{bmatrix}

所以，完整的矩阵乘法就为：

AB=[0−110][01−1111]=[−1−1−101−1] AB=\begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}\begin{bmatrix} 0&1&-1 \\ 1&1&1 \end{bmatrix}=\begin{bmatrix} -1&-1&-1 \\ 0&1&-1 \end{bmatrix}

通过上边的不同计算，可以发现矩阵乘法有以下规则：

若矩阵AA的维度是m×nm\times n，矩阵BB的维度是n×pn\times p，那么矩阵AA和矩阵BB的乘积ABAB的维度是m×pm\times p。ABAB可以进行矩阵乘法的前提是AA的列数必须等于BB的行数。

矩阵的转置

对一个矩阵AA，维度为m×nm\times n，即AA有m行，n列。矩阵AA的转置，记作ATA^{T} 。ATA^{T}维度为n×mn\times m。

其中ATA^{T}的第i行第j列的元素是AA的第j行第i列的元素。

也就是说如果用aija_{ij} 表示AA中的第 ii 行，第 jj 列。那么它等于ATA^{T}中的元素ajia_{ji} 。

矩阵乘法的两种理解

AB=[0−110][01−1111]=[−1−1−101−1] AB=\begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}\begin{bmatrix} 0&1&-1 \\ 1&1&1 \end{bmatrix}=\begin{bmatrix} -1&-1&-1 \\ 0&1&-1 \end{bmatrix}

列向量视角

观察我们上边的矩阵乘法，矩阵AA代表线性变换，类似函数。矩阵BB是一组列向量的集合，类似函数的输入。矩阵乘法的结果就是函数的输出。这种理解就是用B里的列向量的分量对A里的列向量进行线性组合。也就是从列向量的角度去理解矩阵乘法。

行向量视角

另一种不同的视角也很重要，它是行向量视角。因为在深度学习里这种视角更常用。同样是上边ABAB的矩阵乘法。可以把矩阵AA看做由两个2维行向量构成，矩阵BB看做两个3维行向量构成。

在行向量视角里，BB矩阵代表线性变换，类似函数。BB的第一行代表将二维行向量里的 i 向量[1,0]，经过线性变换后称为[0,1,-1]。BB的第二行代表将二维行向量里的 j 向量[0,1]，经过线性变换后称为[1,1,1]。 在行向量视角里，AA矩阵里有两个待变换的行向量，类似函数的输入。第一个行向量[0,-1]，经过矩阵BB线性变换后，生成了结果里的第一个行向量[-1,-1,-1]。第二个行向量[1,0]，经过矩阵BB线性变换后，生成了结果里的第二个行向量[0,1,-1]。

2.3.3 深度学习里的矩阵

矩阵在深度学习里有两种作用，一种是存储数据向量，比如你收集的多个学生的年龄，身高，体重。[12,154, 52]。每条数据是矩阵里的一个行向量。数据矩阵可以理解为它是函数的输入。 还有一种是存储参数，可以理解为它是一个函数，对输入向量进行线性变换。

results matching ""

    No results matching ""