4.9 极大似然估计

假如你在街上碰到一个小摊可以玩游戏，老板告诉你他的箱子里有一样多的白球和黑球。如果你抽中白球，他给你10元，如果你抽中黑球，你给他5元。听起来很划算，你决定试一试。第一次，你抽到黑球，然后放回箱子，再抽。你连续抽了10次，8次是黑球，2次是白球。结果你给了老板20元离开。

请问你现在觉得箱子里白球和黑球一样多吗？相信你现在肯定觉得自己被骗了，箱子里肯定黑球比白球多。如果你是这么想的，那么你实际上就已经不自觉的进行了一次极大似然估计。

之前我们求概率是已知分布，求某个事件发生的可能性。而我们上边的例子是已知一个事情发生了（抽到8次黑球，2次白球），求概率分布（箱子里黑球和白球的分布）。

似然函数就是把概率分布的参数作为未知变量，描述事件发生可能性的函数。

我们假设抽到黑球的概率为a，则抽到白球的概率为（1-a）。则抽到8次黑球，2次白球的似然函数为：

$L(a)=a^8(1-a)^2$ (式4-5)

注意这里抽到黑球的概率a为变量。a作为自变量，抽到8次黑球，2次白球事件的概率作为因变量。上式中的函数L(a)就是似然函数，我们可以绘制出这个函数的曲线。

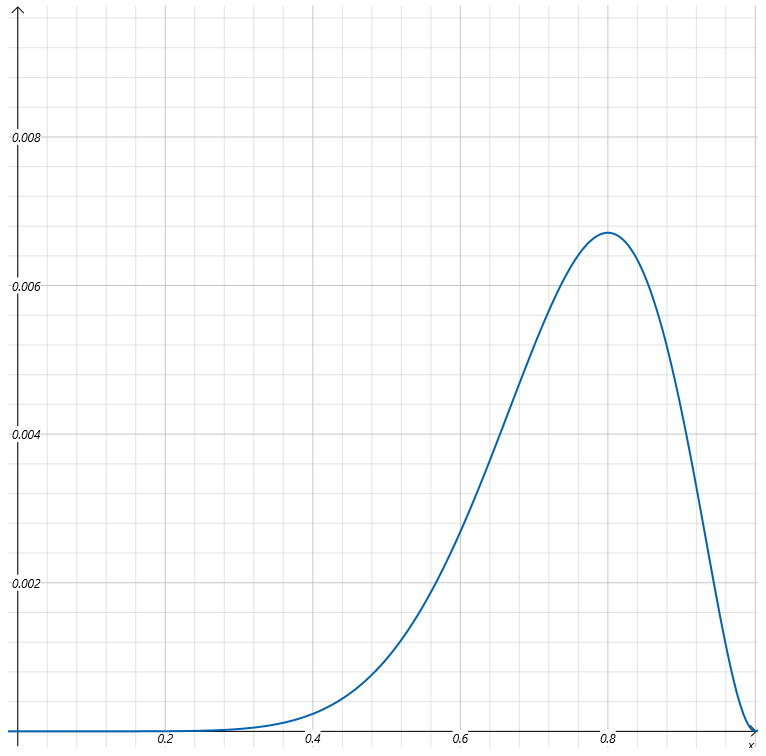
因为a为概率，它的取值只能在0到1之间。所以上图我们只取了a在0到1之间似然函数的图像。

上边我们列出了连续抽了10次，8次是黑球，2次是白球这个事件的似然函数，式4-5。这个事件已经发生了，似然函数表达了不同的分布参数让这个事件发生的可能性。自然我们会想到，最有可能的参数必然是让事件发生可能性最大的那个参数。

通过观察上图，我们可以看到当a取0.8时，似然函数取最大值。也就是说，基于观察结果，箱子里的球有80%是黑球，是最有可能让事件发生的。

因为似然函数一般都是多个概率相乘，多个数值相乘在进行极大值计算时不方便，一般会对似然函数取对数。因为对数运算时一个单增函数，不会改变原函数的极值。同时，对数运算和将多个数相乘，变化为多个数相加。这就大大简化了求极值的过程。

我们对式4-5求对数。

$ln(L(a))=ln(a^8(1-a)^2)=8lna+2ln(1-a)$

我们知道，函数如果可导，则取极值时，导数为0。我们用上式对a求导，并让其等于0，来解出a。

$8\frac{1}{a}-2\frac{1}{1-a}=0$

$\Rightarrow \frac{8}{a}=\frac{2}{1-a}$

$\Rightarrow 8-8a=2a$

$\Rightarrow 10a=8$

$\Rightarrow a=0.8$

下边我们给出极大似然估计的定义。

极大似然估计（Maximum Likelihood Estimation，简称 MLE）是一种统计方法，用于估计模型参数，使得在已知数据样本的情况下，模型生成这些数据的概率最大。

核心思想

假设我们有一个参数化的概率模型，其参数为θ，观测到的数据为 $X=\left \{x_1,x_2,...,x_n \right \}$ 。极大似然估计的目标是找到一个参数 $\hat{\theta}$ ，使得这些观测数据在模型下出现的可能性最大，即最大化似然函数：

$L(\theta | X)=P(X|\theta)=\prod_{i=1}^{n}P(x_i|\theta)$

其中：

为了计算方便，通常取对数，将似然函数转换为对数似然函数：

$\ell(\theta|X)=logL(\theta|X)=\sum_{i=1}^{n}P(x_i|\theta)$

极大似然估计的目标就变为最大化对数似然函数 $\ell(\theta|X)$ 。

极大似然估计