4.3 随机变量及其分布

4.3.1 什么是随机变量

我们投掷一枚硬币，它的样本空间为{正面，反面}。我们去做核酸检查，它的样本空间为{阴性，阳性}。检测一个零件，它的样本空间为{合格，不合格}。不同的实验，有不同的样本空间。但是在研究概率问题时，它们都是同一类问题。都是一个实验结果有2种可能的实验。

为了对同类型的随机实验进行数学抽象，引入了随机变量。它将样本空间里的样本点映射到一个实数。所以随机变量是一个函数。

比如我们把投掷硬币的正面映射为0，反面映射为1。核酸检测的阴性映射为0，阳性映射为1。零件合格为0，不合格为1。这里的数字你可以随意设置，只要能将样本点映射到一个实数就可以。

有的随机实验结果本来就是一个实数，比如测量同学的身高，或者投掷一个骰子。一般情况下就用实验结果作为随机变量映射的实数。

下边给出随机变量的正式定义：在随机实验E中，S是相应的样本空间，如果对S中的每一个样本点 $\omega$ ，有唯一一个实数 $X(\omega)$ 与它对应，那么就把这个定义域为S的单值实值函数：

X=X(\omega)

称为是随机变量。一般用大写字母X，Y，Z表示。

4.3.2 离散随机变量分布

概率质量函数

对于随机变量的值域是离散型的随机实验，比如投掷硬币。如何描述呢？

最简单的办法，就是逐个给出每个样本点的概率取值。比如通过随机变量X将正面映射为0，反面映射为1。

P(X=0)=0.5

P(X=1)=0.5

P(X\notin [0,1])=0

它叫做概率质量函数，数学上定义为：

P(X=x)=p(x)

其中：

x是随机变量X的一个可能的取值
p(x)是X取值x的概率。

它满足三个性质： 1. 非负性：对于所有x，都有 $p(x)\ge0$ 。 2. 归一性：所有可能取值的概率和为1。即： $\sum_{x}^{} p(x)=1$ 3. 如果x不是X的可能取值，则 $p(x)=0$ 。

累积概率分布函数

对于投掷骰子而言，随机变量X的可能取值为{1,2,3,4,5,6}。通过定义上边的概率质量函数，我们可以知道每种取值的概率。但有时候我们在意的是取值小于某个值的概率。比如骰子点数小于等于4的概率。它就是X取值为{1,2,3,4}的概率和。这就是累积概率分布。

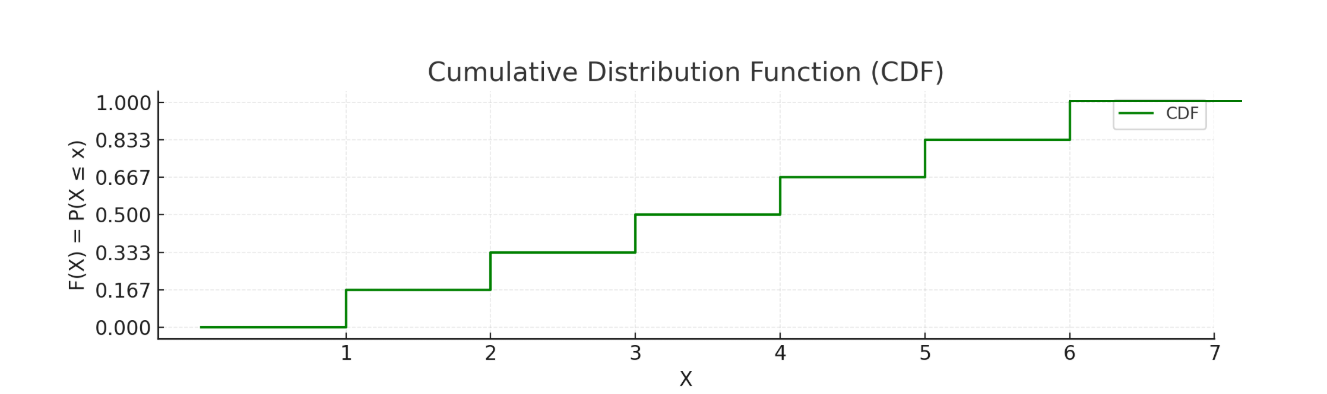
上图为投掷一个骰子的累积概率分布函数，通过它我们可以得到骰子点数大于2，小于等于4的概率。那就是用x=4的累积概率值减去x=2的累积概率值。

它的数学定义为：

给定一个随机变量X，对任意实数 $x\in(-\infty,+\infty)$ 称函数 $F(x)=P(X\le x)$ 为随机变量X的累积概率分布函数。并且对于任意满足条件 $-\infty<a<b<+\infty$ 的实数a,b，有：

P(a < X \le b)=F(b)-F(a)

4.3.3 连续随机变量分布

对于像测量一个班同学每个人的身高，或者测量一批零件每个的重量，得到的结果是连续型随机变量。因为你无法事先列举所有可能的结果。比如人的身高是映射到从0到正无穷这整个区间上的。

因为结果是无穷多个的，我们无法列举每个样本点的概率值。

比如我们要进行一个随机试验，随机从一个高中里选取1000名学生，对他们进行身高测量。得到了随机变量X的1000个值。因为身高是个连续值，取值有无限种可能。有可能再对一个新的学生进行身高测量，结果并不在这1000个测量值中。那么，我们如何利用现在已有的这1000个观测值，来估计一个新学生的身高呢？

概率密度函数

一种解决办法是对这1000个观测值按区间进行统计：

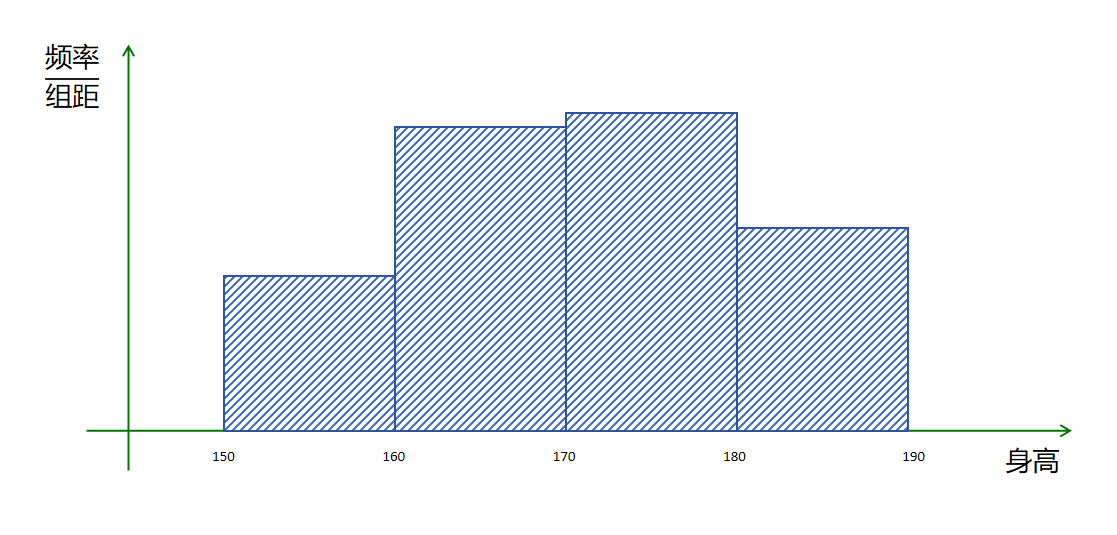
对于身高在150-160区间的人数有170个。除以总数1000，得到随机采样落到这个区间的频率为0.17。

对于身高在160-170区间人数有300个，频率为0.3

对于身高在170-180区间的人数有330个，频率为0.33

对于身高在180-190区间的人数有200个，频率为0.2

可以看到4个区间的频率和为1。更近一步，我们用频率值除以每个分组的组距。这样做的目的是让所有区域的面积和为1。因为我们每个组距为10。所以：

区间	频率	频率/组距	面积
150-160	0.17	0.017	0.17
160-170	0.3	0.03	0.3
170-180	0.33	0.033	0.33
180-190	0.2	0.02	0.2

为什么要让面积和为1。因为一个概率分布的概率和必须为1。这样我们就可以估算一个高中生身高的概率了。我们可以说一个高中生身高在150-160厘米间的概率为0.17，在160-170的概率为0.3，在170-180间的概率为0.33，在180-190之间的概率为0.2。

根据上边的做法，我们更进一步，按5厘米分一个块，这样我们对高中生身高的估算就更加准确了。

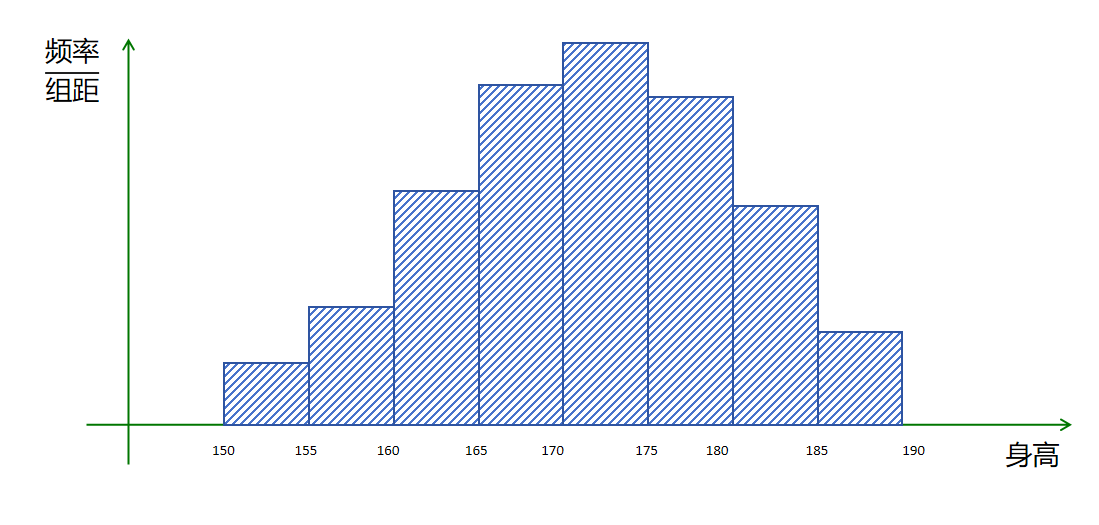
上边的图，可以对一个高中生的身高按照5厘米一个分段来估算概率了。

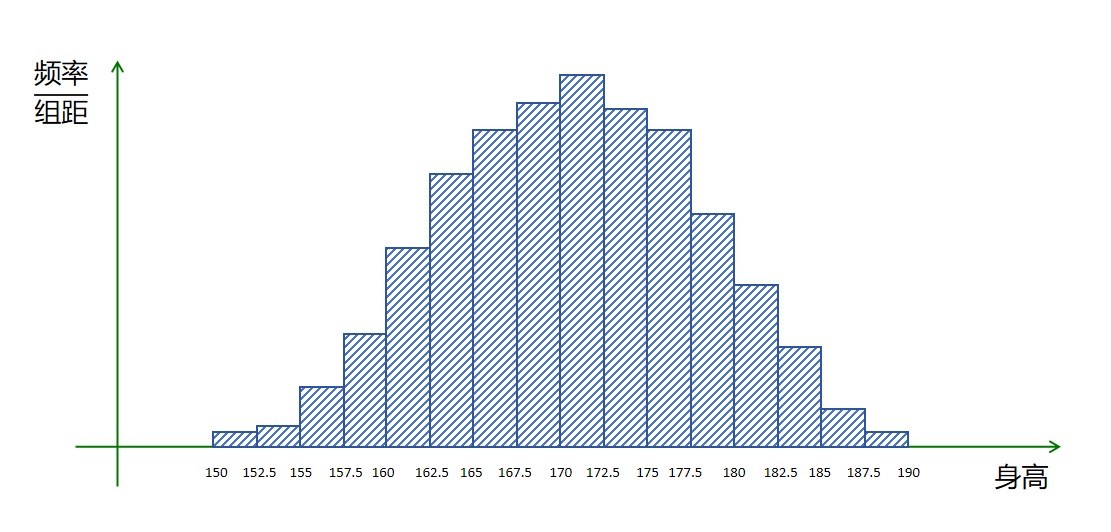
更加细分，可以按照2.5厘米一个间隔估算概率了。

聪明的你肯定想到，如果随机试验的人无穷大，间隔分的无穷小，就可以得到一个分布如下：

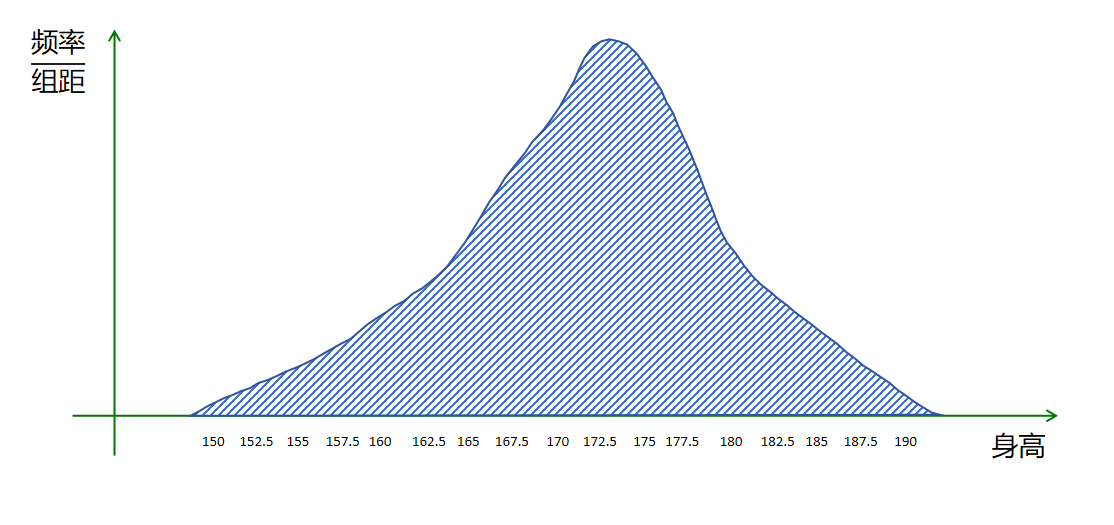
这样我们就得到了连续性变量的概率密度曲线。它形象的刻画了在不同取值区间的概率大小。并且它的面积为1。

概率密度函数（Probability Density Function, PDF）是描述连续型随机变量概率分布的重要工具。概率密度函数 $f(x)$ 是一个非负函数，用来描述随机变量在某一点附近取值的“相对可能性”。

对于连续型随机变量X，其概率密度函数 $f(x)$ 满足以下条件：

非负性： $f(x) \ge 0$ 对所有x都成立。
归一化：总概率为1。 $\int_{-\infty}^{\infty} f(x) \, dx = 1$

连续型随机变量X，其结果取一固定值的概率为0。你可以想象，你随机找一个高中生，他的身高为精确的172.322342的概率为0。其结果取一个区间的概率为：

P(a<X<b) = \int_{a}^{b} f(x) dx

累积概率分布函数

与离散随机变量相同，连续型变量也有累积概率分布函数。定义也是类似：

累积分布函数F(x)表示随机变量X小于或者等于某个值x的概率：

F(x) = P( X \le x)

对于连续型随机变量，F(x) 是通过概率密度函数f(x)的积分来定义的：

F(x)=\int_{-\infty}^{x} f(t) \, dt

对于同一个随机变量X的概率密度函数 $f(x)$ 与累积概率分布函数 $F(x)$ 有如下关系：

f(x) = \frac{dF(x)}{dx}

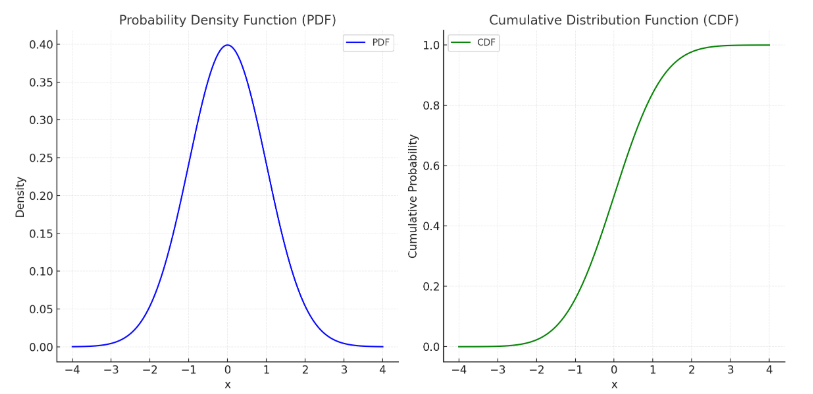
上图左边为正态分布的概率密度函数，右图为正态分布的累积概率分布函数。

随机变量及其分布