4.6条件概率与全概率

以你出门带伞这件事为例，在不同的条件下，你带伞的概率会不同。比如天气预报说今天是晴天，你带伞的概率就比较低，而如果天气预报说今天有可能下雨，那么你带伞的概率就会增加。条件概率就是研究在提供某些条件下，事件发生的概率。

在事件B发生条件下，A事件发生的概率表示为：

P(A|B)

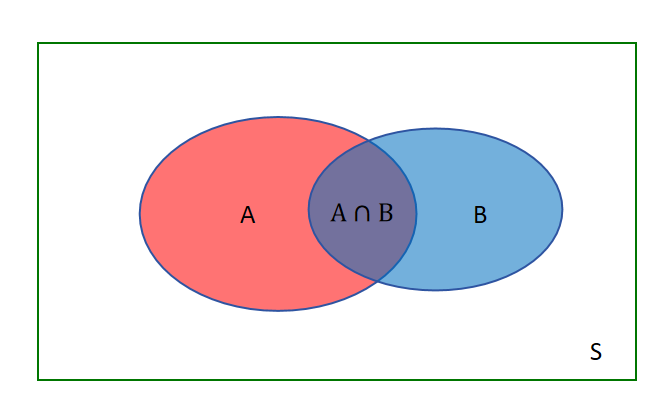
以上图为例，样本空间S，我们想要知道在事件B发生的情况下，A发生的概率。那怎么求呢？通过观察图可以知道，就等于A交B的面积（概率）除以B的面积（概率）。

所以：

P(A|B)=\frac{P(AB)}{P(B)};P(B)\ne 0

条件概率的本质是，额外的条件让事件的样本空间变小。原始P(A)的样本空间是S，而P(A|B)同样是求A的概率，但是样本空间变成了B。

假设投掷一个等概率的骰子。得到奇数的概率为 $\frac{1}{2}$ ，得到奇数，并且为3的概率为 $\frac{1}{6}$ 。那么问题是如果已知一次投掷结果是奇数，那么是3的概率为多少呢？

已知投掷结果为奇数，那么样本空间就从原来的{1,2,3,4,5,6}，缩小到了{1,3,5}。在这个缩小的样本空间里，得到3的概率就为1/3。

当然，也可以根据条件概率公式来求：

P(A|B)=\frac{P(AB)}{P(B)}=\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{3}

如果问你P(A) 和 P(A|B) 那个概率大？根据定义 P(A|B) 也是求A事件发生的概率，不过是给事件A发生提供了额外的信息，也就是B发生。我们看以下这个例子：

一个等概率的骰子，你投掷得到3的概率有多大呢？答案是 $P(A)=\frac{1}{6}$ 。

假如告诉你投掷得到的是奇数，那么投掷得3的概率有多大呢？答案是 $P(A|B)=\frac{1}{3}>P(A)$ 。

假如告诉你投掷得到的是偶数，那么投掷得3的概率有多大呢？答案是 $P(A|B)=0<P(A)$ 。

假如告诉你投掷得到数大于0，那么投掷得3的概率有多大呢？答案是 $P(A|B)=\frac{1}{6}=P(A)$ 。

可见 P(A) 和 P(A|B) 的大小是没有关系的，也就是说提供B事件发生的信息，对于A事件发生可能是有帮助作用，也可能是反作用，也可能没有作用。

根据条件概率公式变换可得：

P(AB) = P(A|B)P(B)

这个公式也很好理解，B事件代表下雨，A事件代表你打伞。下雨天并且你打伞的概率就等于下雨的概率，乘以下雨天你打伞的概率。符合概率多步事件的乘法法则。

先看一个例子，假如我每天上班有0.3的概率开车，0.5的概率骑自行车，0.2的概率步行。开车有0.1的概率迟到，骑自行车有0.2的概率迟到，步行有0.05的概率迟到。那么我迟到的概率为多少呢？

我完成上班这件事一共有且只有3种方式，开车，骑自行车，步行。那么我上班迟到的概率就应该是开车并且迟到的概率+骑自行车并且迟到的概率+步行并且迟到的概率。所以，我迟到的概率就为：

0.3\times0.1+0.5\times0.2+0.2\times0.05 = 0.14

全概率公式就是更加规范化的描述了我们上边的计算过程。

完备事件组，又称为样本空间的分割或者划分。如果一组事件他们两两互斥，并且合集为整个样本空间。那么它们就是一个完备事件组。

比如投掷骰子得到偶数和得到奇数的事件。或者投掷骰子小于3和大于等于3的事件。都是一个完备事件组。

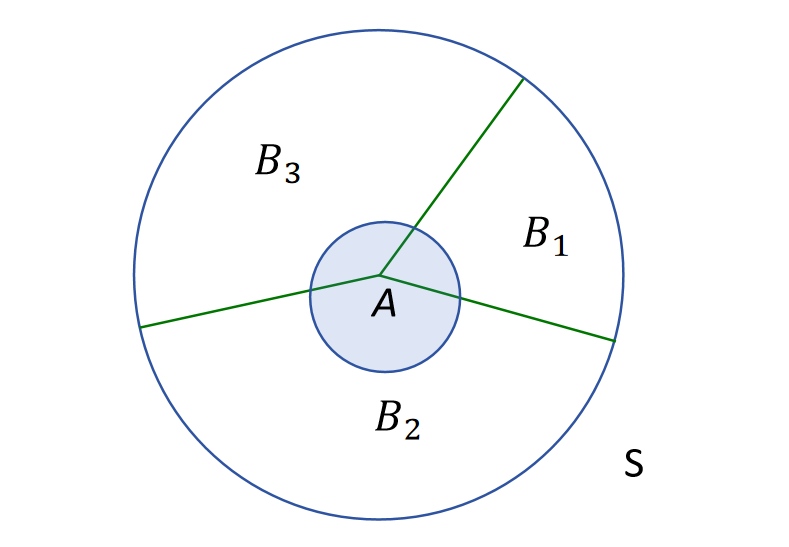
假设样本空间为S， $B_1,B_2,B_3$ 为S的一个完备事件组，则：

$P(A)=P(AS)$

$=P(A(B_1\cup B_2 \cup B_3))$

$=P(AB_1\cup AB_2 \cup AB_3)$

$=P(AB_1)+P(AB_2)+P(AB_3)$

$=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+P(A|B_3)P(B_3)$

全概率公式：

设 $B_1,B_2,...,B_n$ 为样本空间S的一个完备事件组，且 $P(B_i)>0(i=1,2,...,n)$ ，则对任意事件A有：

P(A) = \sum_{i=1}^{n} P(A|B_i)P(B_i)

条件概率与全概率