3.9 定积分

3.9.1 定积分的由来

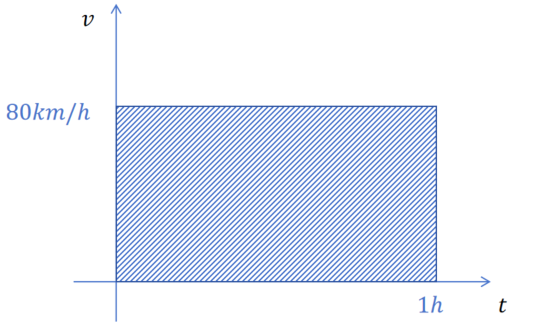
假如你开着一辆车，以80千米每小时的速度匀速前进，开了1个小时，那么你行驶的路程是多少？ 答案是：

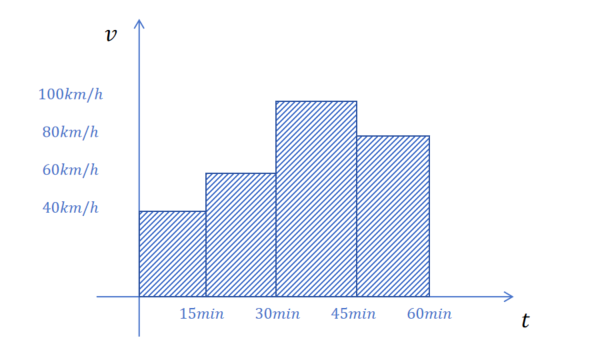
一直以相同速度行驶，实在无聊。前15分钟你以40千米每小时行驶，接下来15分钟以60千米每小时行驶，接下来15分钟以100千米每小时行驶，最后15分钟以80千米每小时行驶，那总共行驶的路程是多少？

答案也不难计算：

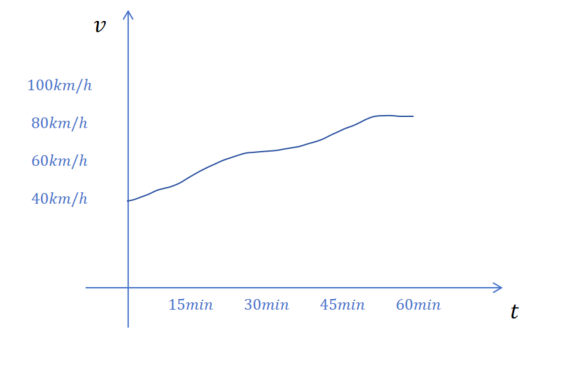
更现实的情况是，你行驶了一个小时，但是行驶的速度一直在变化，那该怎么计算呢？

还是利用微积分里的重要思想，以直代曲。把这一个小时划分成无数个时间片段，每个时间片段里选取任一时刻的速度作为这个时间片段的平均速度。然后用时段平均速度乘以时段时间，就代表这个时段行驶的路程。最终把所有时段行驶路程加起来就是总共行驶的路程。可以想象，时间片段划分的越小，这个估算越准确，当所有划分的时间片段里最大的时间片段都趋于0时，就可以得到真实的行驶路程了。

上边这个思想就是定积分的思想。

3.9.2 定积分的概念

把上边对可变速度看做由一个函数$f(x)$来决定，x是时刻，$f(x)$是时刻x时的速度。用标准的数学语言描述积分就为：

设$f(x)$在[a,b]上有界，在[a,b]中插入若干个分点：

把区间[a,b]分成n个小区间，各个小区间的长度依次为：

在个小区间上任取一点$\xi_i(\xi_i\in[x_{i-1},x_i])$，作乘积$f(\xi_i)\triangle x_i(i=1,2,...)$，并求和

记$\lambda = max\left \{ \triangle x_1,\triangle x_2,...,\triangle x_n \right \}$，不论对[a,b]怎么划分，也不论在小区间$[x_{i-1},x_i]$上的点$\xi_i$怎么选取。只要当$\lambda \to 0$时，和$S$总是趋向于特定的极限$I$,我们称这个$I$为函数$f(x)$在区间[a,b]上的定积分，记作：

即：

3.9.3 定积分的计算

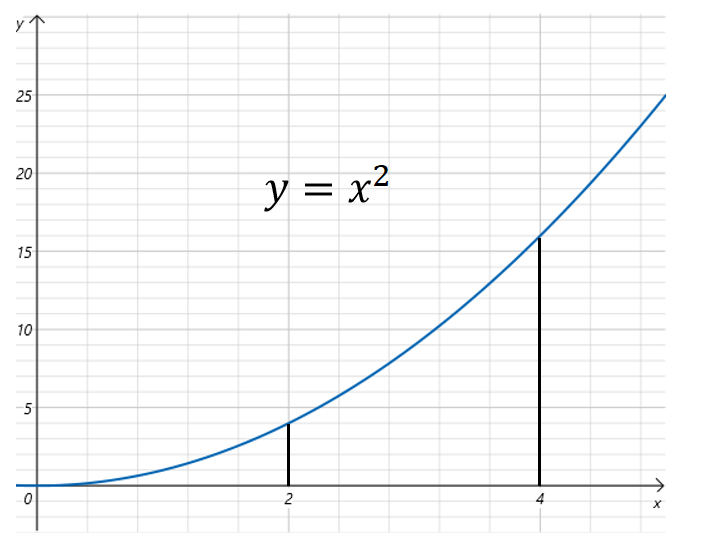
假设汽车的行驶速度y(km/h)满足方程$y=x^2$,x为小时。那么问汽车在第2小时到第4小时之间行驶过的路程怎么算？

根据定积分的定义，这就是求

根据积分的定义，很难算出结果。我们换个思路来考虑，我们可以用汽车在第4小时行驶的总里程减去汽车在第2小时行驶的总里程来计算，这样就简单了很多。

但问题是我们目前只知道汽车瞬时速度随时间变化的函数，不知道路程随时间变化的函数。没有关系，根据我们之前学过的导数的定义，我们知道瞬时速度是路程对时间的导数。

那我们只需要找到哪个函数的导函数是速度函数$f(x)=x^2$，那样就得到路程随时间变化的函数了（称它为导函数的原函数）。不难得到原函数为：

有了汽车里程随时间变化的函数，我们用4时的里程减去2时的里程，就得到了积分的结果：

通过这道题，我们可以得到计算定积分的公式（牛顿-莱布尼茨公式）：

如果函数$F(x)$是连续函数$f(x)$在区间[a,b]上的一个原函数，则：