7.3多元逻辑回归

我们在讲逻辑回归时说过，逻辑回归就是在线性回归的计算结果上，增加了一个Sigmoid激活函数。

LogisticRegression(x)=Sigmoid(LinearRegression(x))=Sigmoid(wx+b)

我们再来复习一下逻辑回归的函数曲线：

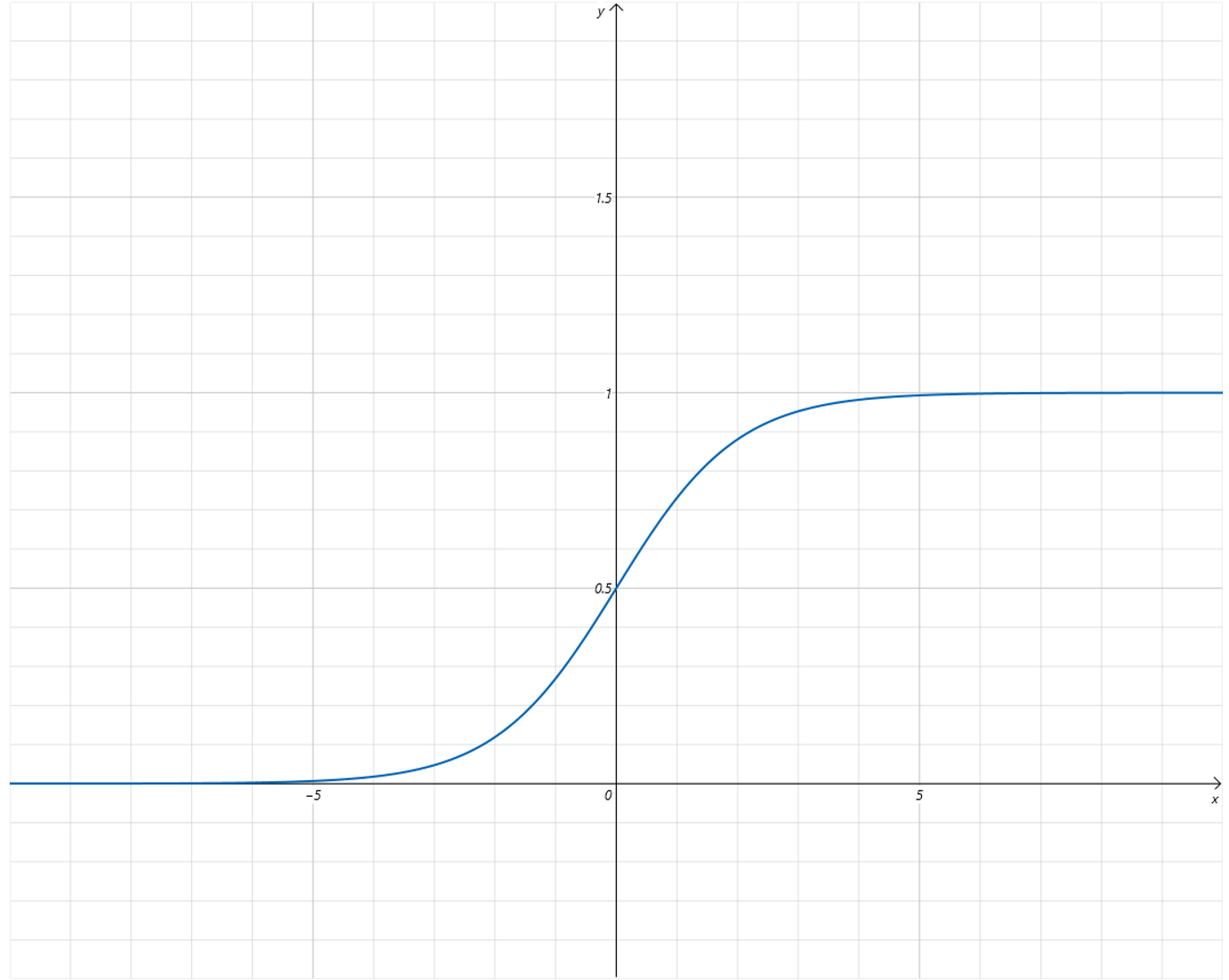
Sigmoid这个激活函数的作用可以将大于0的数快速映射到接近1，小于0的数快速映射到接近0。

在逻辑回归里，Sigmoid函数的输入是线性回归的结果，所以线性回归的作用，就是将Feature通过参数w和b的线性变化，让正例的线性变化结果大于0，让负例的线性变化结果小于0。再由Sigmoid函数将线性回归的结果映射到0-1之间。

多元逻辑回归，就是将一元逻辑回归中的一元线性回归部分，升级为多元线性回归。然后还是对线性回归的结果应用Sigmoid激活函数。

LogisticRegression(x_1,x_2,...,x_n)=Sigmoid(LinearRegression(x_1,x_2,...,x_n))=Sigmoid(w_1x_1+w_2x_2+...w_nx_n+b)

多元逻辑回归中，多元线性回归部分，将多个Feature通过对应的参数w以及b进行线性变化，让正例的多元线性变化结果大于0，让负例的多元线性变化结果小于0。最后同样由Sigmoid函数将线性回归的结果映射到0和1之间。

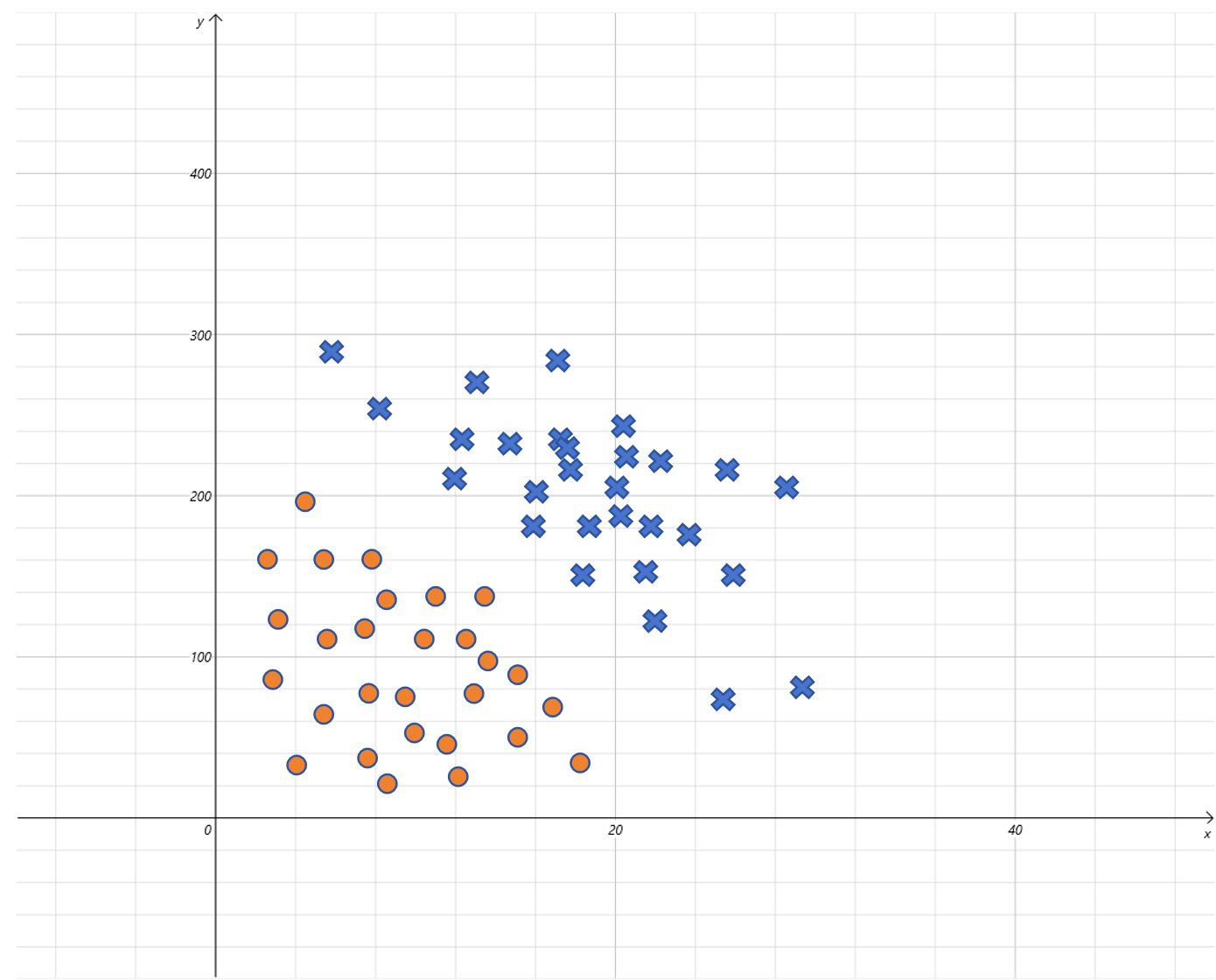
比如上图是小明是否出门与气温（x轴）和PM2.5（y轴）的关系图。就可以构造一个二元逻辑回归来建模。输入由两个特征气温和PM2.5的值，预测出门为1，不出门为0。它的假设函数就为：

Sigmoid(w_1x_1+w_2x_2+b)

其中

x_1

代表气温，

w_1

是气温的权重，

x_2

代表PM2.5的值，

w_2

代表PM2.5的权重，b是线性回归的偏置。 ###7.3.3逻辑回归的决策边界逻辑回归内部是一个线性回归，然后通过Sigmoid函数，线性回归大于0的结果，映射到1，小于0的结果映射到0。线性回归只能是一条直线。我们之前举的例子里，逻辑回归的决策边界都是直线。那么逻辑回归的决策边界只能是直线吗？

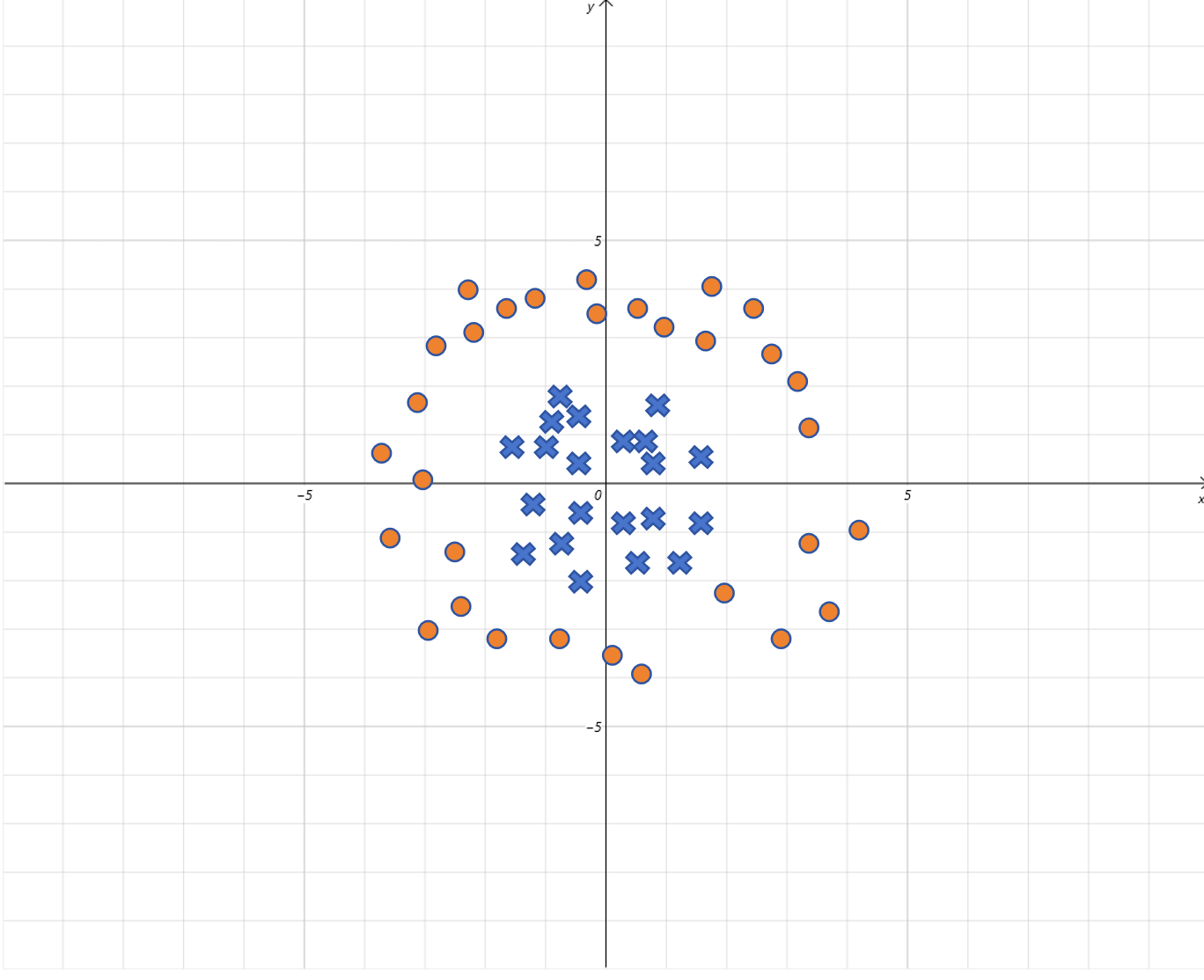
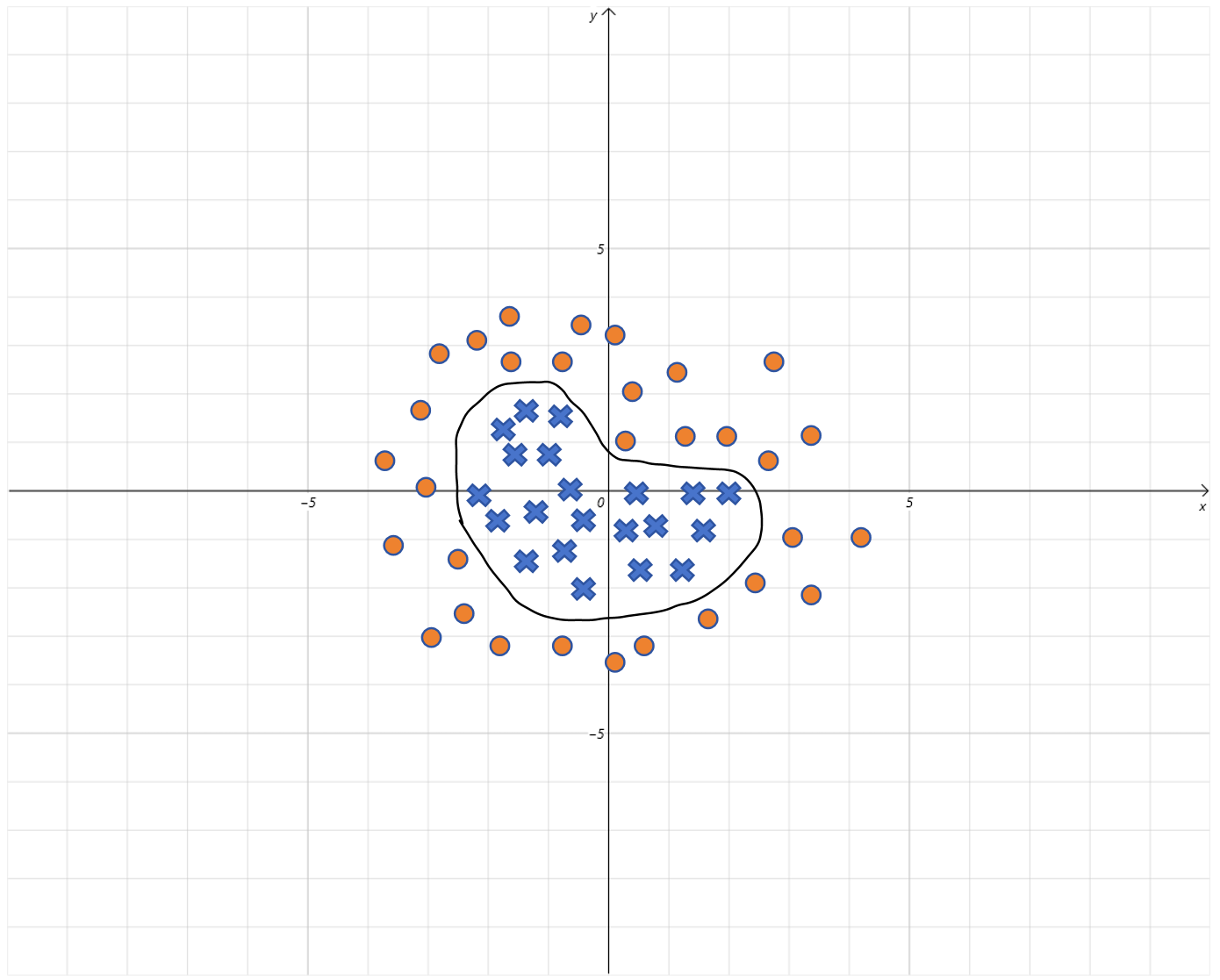
比如像上图中，输入特征有2个，分别用x轴和y轴表示，同样是进行二分类。但是它的决策边界不是直线。逻辑回归可以解决这样的问题吗？答案是肯定的。

还记得我们之前让线性回归拟合曲线的办法吗？对，通过构造高次项的特征就可以让线性回归拟合曲线。同样的，这里通过给逻辑回归里的线性回归部分增加高次项，同样可以解决曲线决策边界的问题。

Sigmoid(w_1x_1^2+w_2x_2^2+b)

假设通过模型训练，我们得到 $w_1,w_2$ 都等于1，b=-4，带入假设函数：

Sigmoid(x_1^2+x_2^2-2^2)

我们知道圆的方程为：

x_1^2+x_2^2=r^2

所以逻辑回归里线性方程就表示一个半径为2的圆，当图上的点在圆的内部，线性方程的取值就小于0，被Sigmoid函数映射到0附近。当图上的点在圆的外部，线性方程的取值就大于0，被Sigmoid函数映射到1附近。

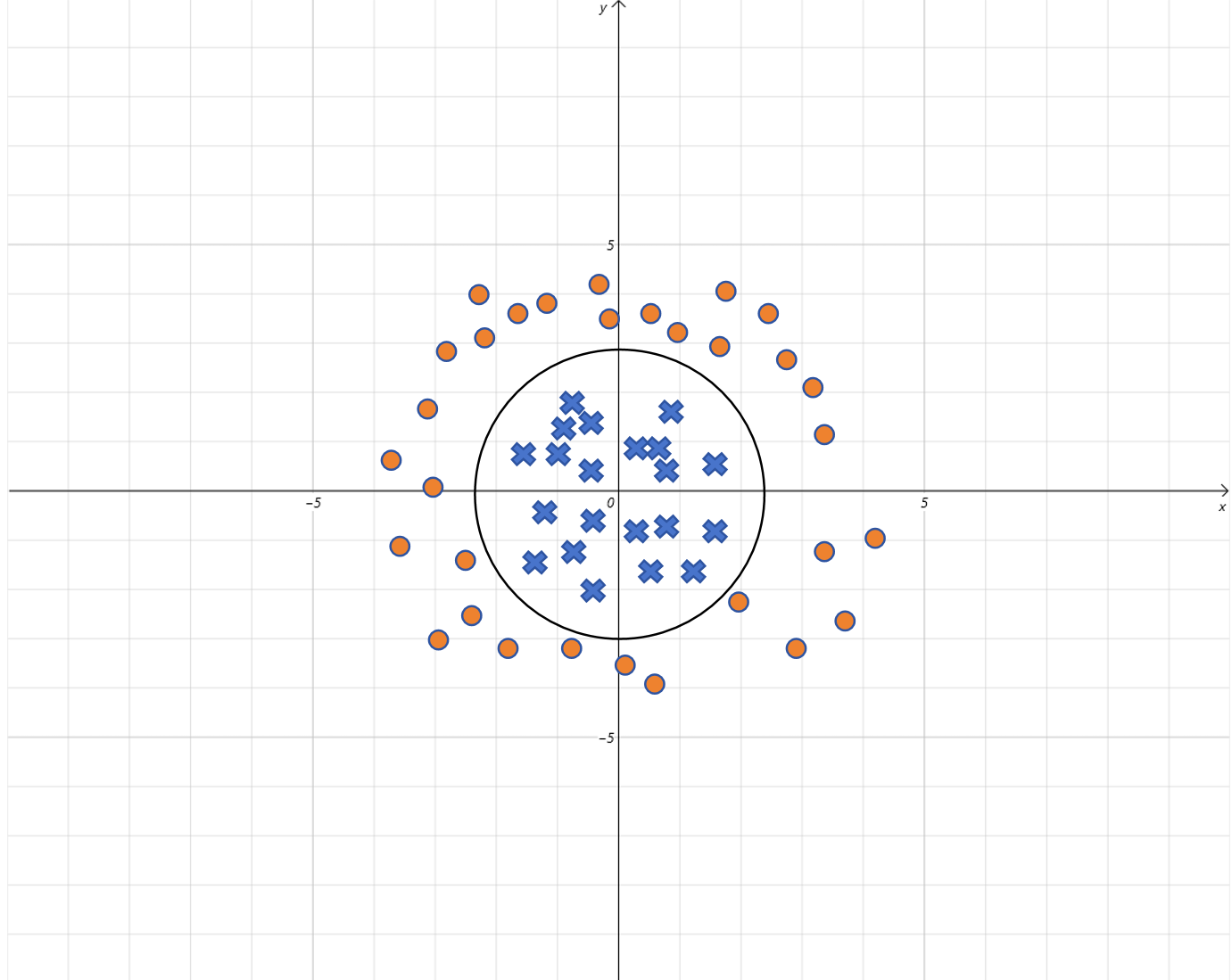
如果你增加更多的高次项，理论上逻辑回归的决策边界可以是任意曲线。

我们上边的例子都是二分类的例子，但是现实生活中有很多分类是多分类。逻辑回归也是可以用来多分类的，最常用的方法，就是1对多方式。

假如要分类的类别为A，B，C，D。

你可以训练4个逻辑回归的模型，它们分别为：

区分A和其他（B，C，D）的二分类模型。以A为正例，Label为1。

区分B和其他（A，C，D）的二分类模型。以B为正例，Label为1。

区分C和其他（A，B，D）的二分类模型。以C为正例，Label为1。

区分D和其他（A，B，C）的二分类模型。以D正例，Label为1。

在预测时，把样本的feature分别输入4个逻辑回归的模型，可以认为每个模型输出的分别是样本类别为A，B，C，D的概率值。取概率值最大的类别作为预测输出即可。

多元逻辑回归