3.2 导数的定义

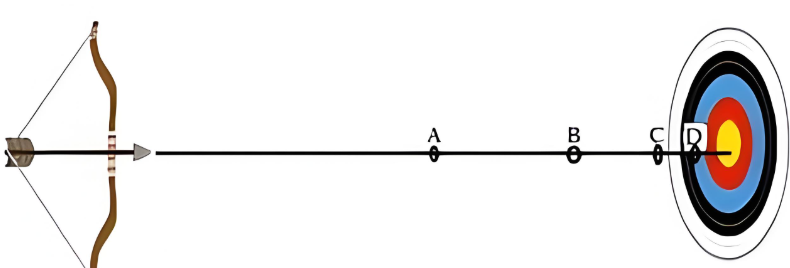
3.2.1 芝诺的飞矢不动论

古希腊哲学家芝诺有一个著名的悖论，他设想了一个情景：

1. 假设一支飞箭正在飞行。

2. 在任意一个瞬间，飞箭在其特定的位置上是静止的，因为在这个瞬间，箭头并没有时间移动到其他位置。

3. 如果每个瞬间箭都是静止的，那么整个过程中，飞箭都是静止的。因此，飞箭永远不会动。

按照芝诺的观点，射出去的箭是静止的。这明显违背常识，但想想好像还有些道理。

3.2.2 汽车的瞬时速度

如果你还在困惑芝诺的飞矢不动论，那么你想想汽车仪表盘上都有汽车的瞬时速度，这是如何获取的呢？我们知道平均速度怎么算，那就是从$t_0$时刻开始，经过一段时间$\triangle t$，行驶了路程$\triangle s$。假设某时刻$t$汽车的总里程为$S(t)$那么平均速度就为：

这时，如果让$\triangle t$趋于0，但不等于零。那么根据上式计算出来的速度就可以认为是$t_0$时刻的瞬时速度。

3.2.3 切线的斜率

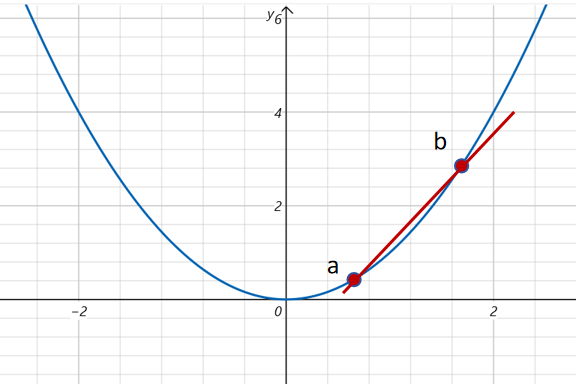
什么是切线呢？

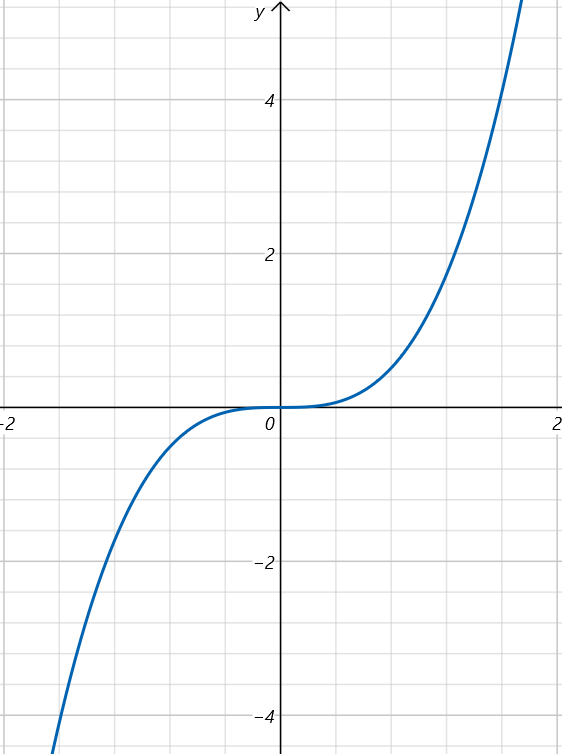
你可能会画出函数在某一点的切线，那到底如何确定函数在某一点的切线呢？你可能会说一条直线，和函数只有一个交点，这个直线就是这个交点的切线。但是我们知道，两点才能确定一条直线。一个点怎么可以确定一条直线呢？ 你可能会说你给不出确定的定义，但是你直觉知道怎么画出一个切线。那么，你知道函数$f(x)=x^3$在（0,0）点的切线是什么吗？

答案是函数$f(x)=x^3$在（0,0）点的切线就是x轴。 下边我们给出切线的严格定义。

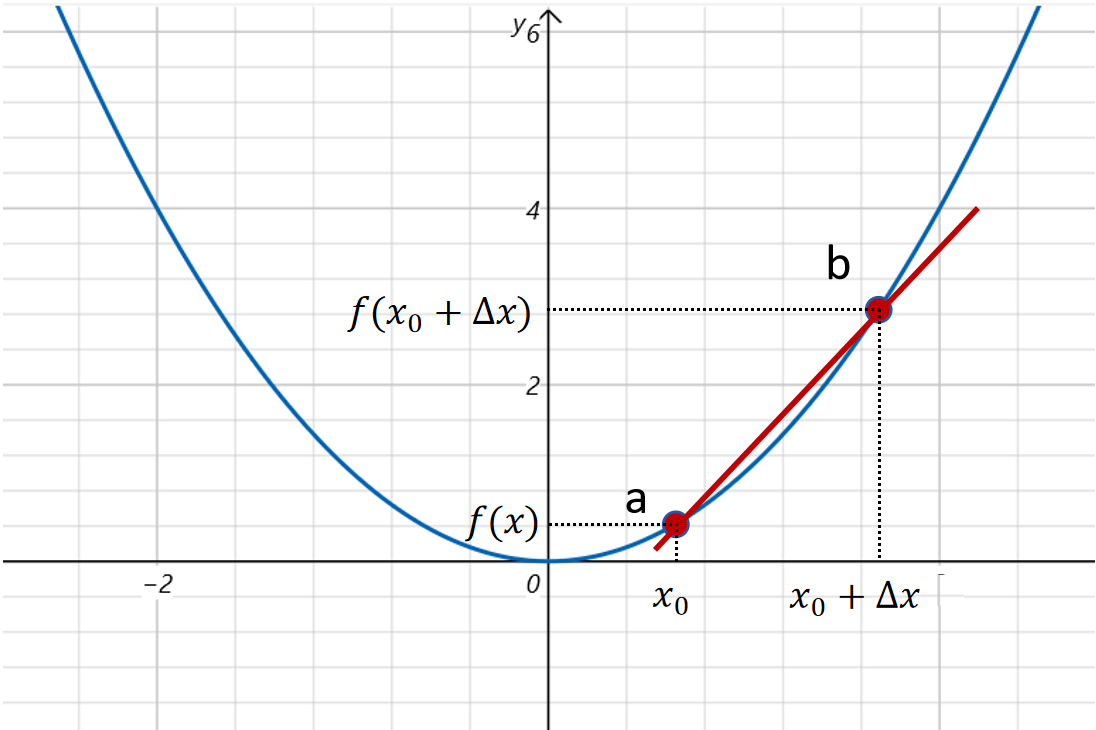
在上图中，如果我们要求a点的切线可以先在曲线上找出另外一点b。然后由a,b两点构成一个直线，然后沿着曲线，移动b，让b无限接近a，但是不和a重合，得到的那条直线就是a点的切线。

有了切线的定义，那如何求a点切线的斜率呢？对于由a，b两点构成直线的斜率计算是：

按照刚才我们对切线的定义，让b无限接近a，也就是让$\triangle x$趋于0。就得到了切线的斜率：

3.2.4 导数的定义

通过上边对瞬时速度和切线斜率的讨论，我们发现式3-1和式3-2非常相似，表达的概念也很类似。

瞬时速度讨论的是位移关于时间的函数在某一点的变化率。

切线斜率讨论的是高度关于长度的函数在某一点的变化率。

数学对这类问题进行了抽象，对所有函数在某一点因变量关于自变量的变化率进行了定义。

如果等式右边的极限存在，则称$f(x)$在$x_0$处可导，导数记作：$f'(x_0)$。如果等式右边的极限不存在，则称$f(x)$在$x_0$处不可导。 你可以再回想一下芝诺的飞矢不动论，函数的自变量取一个固定的值，它的因变量应该是固定的，没有变化率。但是通过导数的定义，就可以利用极限的思想，计算出因变量在自变量取某一个值时的变化率。

3.2.5 导数与连续的关系

函数在某一点的导数存在，则函数在这一点一定连续。因为导数存在，则为一个固定值C。

通过对式3-3进行变换，可得：

$\lim_{\triangle x \to 0}f(x_0+\triangle x) =f(x_0)+ C\cdot\lim_{\triangle x \to 0}\triangle x$

进而可得：

$\lim_{\triangle x \to 0}f(x_0+\triangle x) =f(x_0)$

上式就是函数连续的定义。所以可导一定连续。

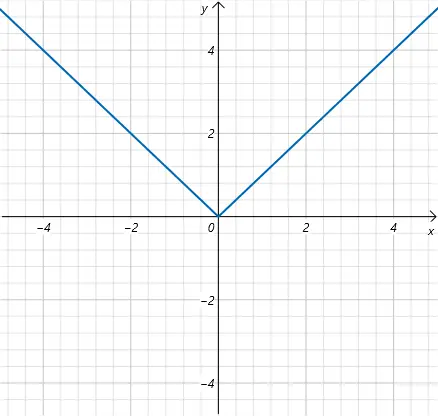
但是连续不一定可导。比如函数：

在$x=0$处不可导。

这里我们先给出函数在某一点可导的充要条件，那就是函数在此点的左导数和右导数都存在，并且左导数等于右导数。

左导数 左导数是自变量从点的左边接近时，研究因变量的变化率。

$f'_-(x_0)=\lim_{\triangle x \to 0^-}\frac{f(x_0+\triangle x)-f(x_0)}{\triangle x}$

右导数 左导数是自变量从点的右边接近时，研究因变量的变化率。

$f'_+(x_0)=\lim_{\triangle x \to 0^+}\frac{f(x_0+\triangle x)-f(x_0)}{\triangle x}$

对于$y=|x|$，它的左导数等于-1，右导数为1，两者不相等。所以它在x等于0处不可导。

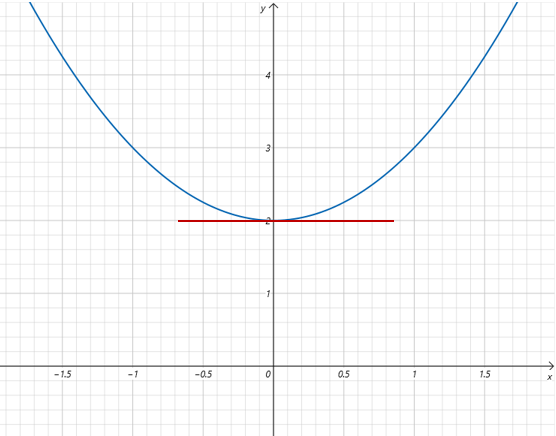
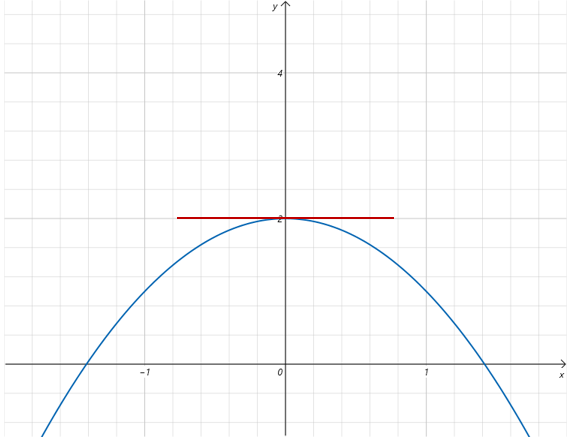
3.2.6 导数与极值的关系

因为如果函数在某点可导，则它在改点的导数，就是该点的切线斜率。通过观察上边两幅图，不难理解当$f(x)$在$x_0$处取得极值，且函数在$x_0$可导，则必有$f'(x_0)=0$。

实际中，经常用导数为0的特性来求函数的极值。

3.2.7 导函数的定义

如果我们需要描述一个函数在每一点的导数，就需要定义导函数。

导函数是一个新的函数，表示原函数在每一点的导数。