2.5 向量叉乘

2.5.1 力矩

我们从一个物理概念来引入向量的叉乘。那就是力矩。

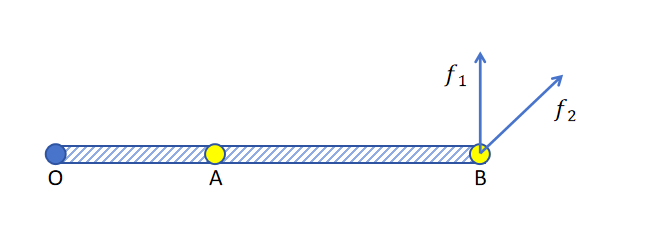
比如上图中，木棍的一端O固定，你要施加一个力来让这个木棍旋转，是A点更容易还是B点更容易呢？有生活经验的你肯定会选择B点。以同样大的力气，沿$f_1$方向让木棍旋转更容易还是沿$f_2$方向让木棍旋转更容易呢？相信你会选择沿$f_1$方向。

物理中描述这种“更容易旋转”的物理量就叫做力矩。力矩与3个因素相关。

力臂的大小 力臂的大小就是旋转点O到力的作用点P之间的长度。相同条件下，力臂越长，力矩越大。旋转越容易。

力的大小 只要力不平行于力臂的方向，相同条件下，力越大，力矩越大。旋转越容易。

力和力臂的角度 力臂大小和力的大小不变的情况下，力和力臂的夹角越接近90°，力矩越大。旋转越容易。而sinθ正好描述了这一关系。sin 0°为0，sin 90°为1。

力矩的定义 所以力矩M的公式为向量P的模长乘以向量F的模长，乘以两个向量夹角的sin值。

$M=|P||F|sin \theta$

2.5.2 向量的叉乘

在线性代数里，我们把类似于力矩这种运算叫做叉乘（叉积，向量积）。用符号$\times$表示。

$a \times b = |a||b|sin \theta$

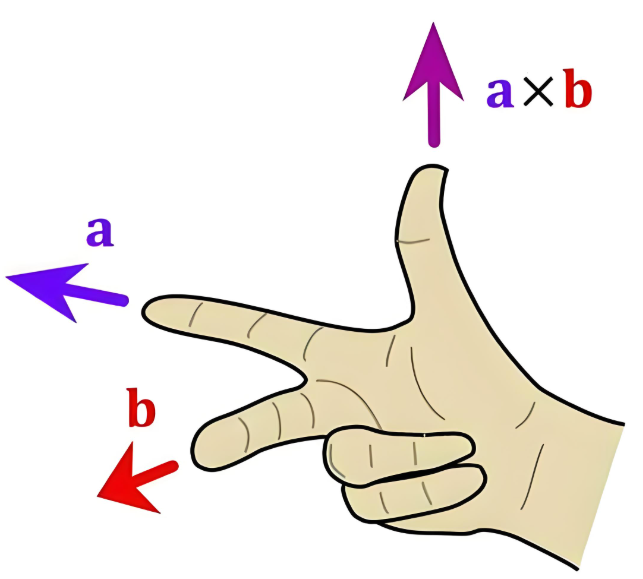
叉乘的方向 力矩是一个向量，它不光有大小，还有方向。因为力矩描述的是使物体旋转的容易程度。但是旋转有可能是顺指针方向，也有可能是逆时针方向。叉乘也是一个向量，有自己的方向。怎么确定这个方向呢？这就要用的右手法则了。

2.5.3 叉乘的计算法则

根据右手法则，$a \times b$ 和$b \times a$的方向是不同的。所以叉乘不满足交换律。

分配率

$(a+b) \times c = a \times c + b \times c$

$c \times (a+b) = c \times a + c \times b$

用力矩可以帮助你理解，两个力在同一个力臂上产生的力矩的和等于它们和力的力矩。

数乘结合率

$(\lambda a) \times b = a \times (\lambda b) = \lambda (a \times b)$

以力矩来理解，不论力或者力臂变为原来的λ倍，力矩也会变为原来的λ倍。

2.5.4 叉乘的计算公式

有了叉乘的计算法则，我们可以把向量a和b用标准基向量加和的方式来表示，推导出叉乘的计算公式。

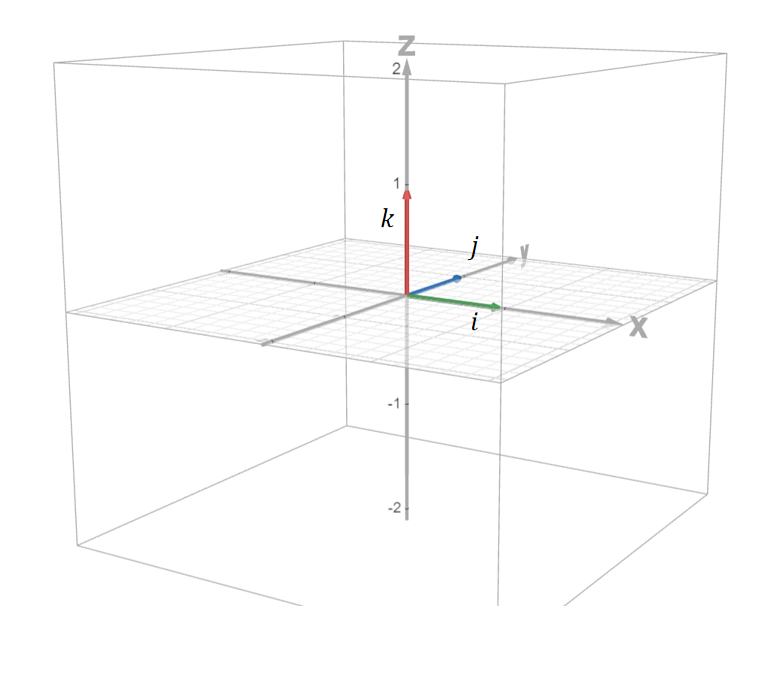
$a = a_xi+a_yj+a_zk, b=b_xi+b_yj+b_zk$

$a \times b=( a_xi+a_yj+a_zk) \times (b_xi+b_yj+b_zk)$

利用叉乘分配率有：

$a \times b=a_xi \times (b_xi+b_yj+b_zk) + a_yj \times (b_xi+b_yj+b_zk) + a_zk \times (b_xi+b_yj+b_zk)$

上式中$a_x,a_y,a_z,b_x,b_y,b_z$都为标量，i,j,k为标准基向量。利用数乘结合律有：

$a \times b= a_xb_x(i \times i)+a_xb_y(i \times j)+a_xb_z(i \times k)+a_yb_x(j \times i)+a_yb_y(i \times j)+$

$a_yb_z(j \times k)+a_zb_x( k \times i)+a_zb_y(k \times j)+a_zb_z(k \times k)$

根据叉乘的定义，标准基向量和自身叉乘为0，因为sin 0°为0。也就是：

$i \times i = 0$

$j \times j = 0$

$k \times k = 0$

另外，根据叉乘的定义，叉乘的结果为向量，结果向量模长为原始两个向量模长的乘积再乘以它们之间夹角的sin值。方向按照右手法则来确定，垂直于原始两个向量构成的平面。

$i \times j = k$

$j \times i= -k$

$j \times k = i$

$k \times j = -i$

$k \times i = j$

$i \times k = -j$

带入上式，最终得到的结果为：

$a \times b = (a_yb_z-a_zb_y)i+(a_zb_x-a_xb_z)j+(a_xb_y-a_yb_x)k$

可以看到，最终的结果为一个向量。

2.5.5 叉乘在深度学习里的应用

在深度学习里的优化算法里用到了梯度下降算法，它是训练深度学习算法能通过对数据的学习，调整模型参数的关键。在证明梯度方向是函数值上升最快的方向时，我们会用到叉乘。到时会用两个向量的叉乘来找到一个同时垂直于这两个向量的向量。