10.2 卷积操作
这一节我们来正式学习卷积核，它的原理和我们上一节讲的探雷器非常相似。
10.2.1 卷积运算过程
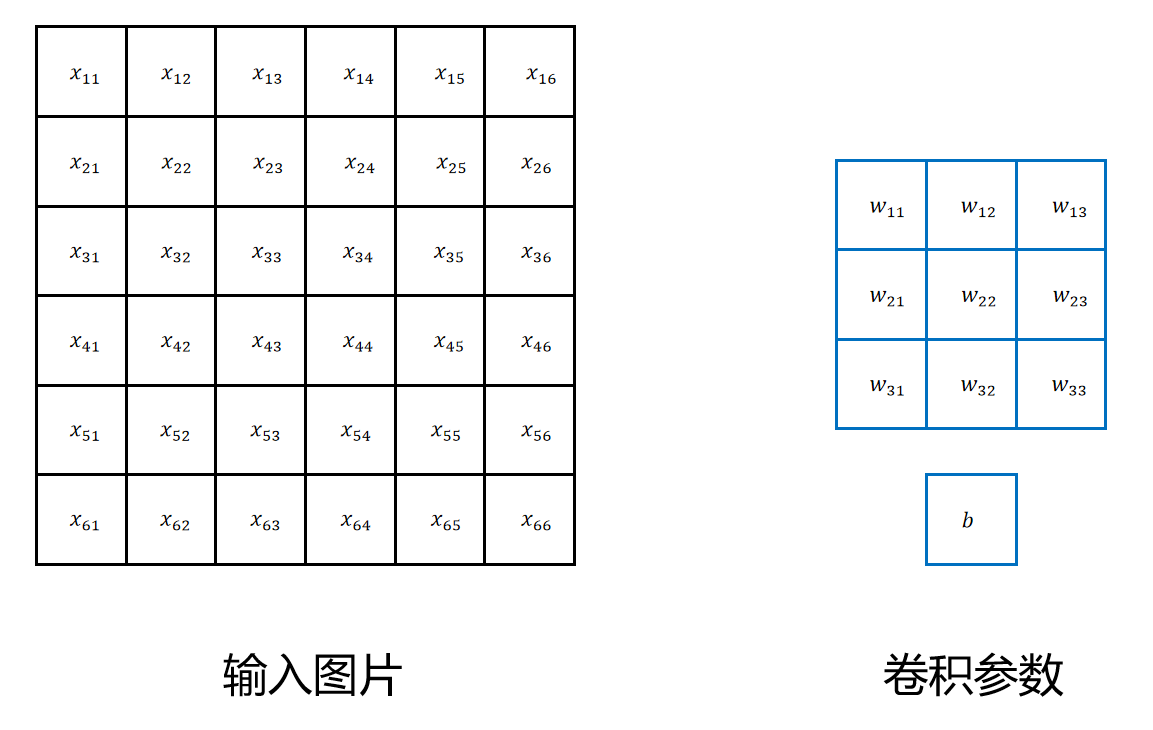首先我们来定义输入和参数。
输入 假设输入是一个照片，它的长和宽都是6个像素。如果它是彩色照片，那么它需要用一个6x6x3的tensor来表示。最后一个维度的3，表示RGB，3个通道（channel）。如果是黑白照片，那么它需要用一个6x6x1的tensor来表示，最后一个维度是1，代表只有一个通道：灰度值通道。下边我们以6x6的黑白照片为例进行讲解。
参数 一个3x3的卷积操作一共有10个参数，包括一个3x3的卷积核参数，还有一个偏置b参数。卷积核和偏置一起被称为一个过滤器（Filter）。
在进行卷积运算时，卷积核从图像的左上角开始，从上到下，从左到右，进行扫描。每次对3x3的像素进行卷积运算。卷积运算对每个位置的像素值和卷积核对应位置的权重相乘，然后累加，最后再加上偏置b，得到z值，然后z值经过激活函数后，得到a值。a值为新的“图片”上的一个“像素”。新的“图片”，我们称为特征图，特征图上的每个“像素”都是从原始图片上提取的一个特征。比如在检测猫的任务中，一个a值可能代表是否在这个卷积区域发现了猫的眼睛。
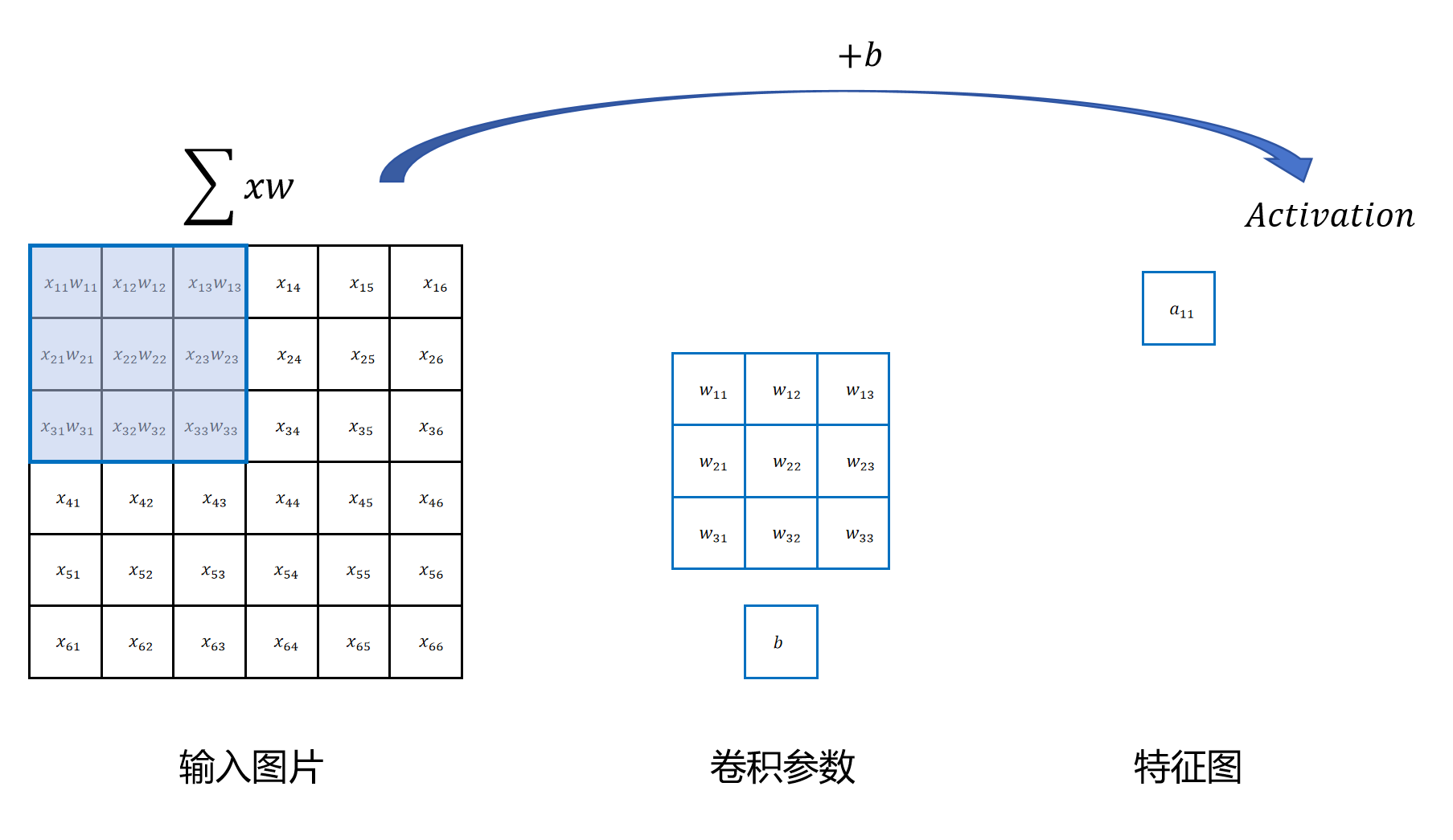
当提取了原始图片的第一个3x3区域的特征后，卷积操作就向右滑动一个像素，然后用同样的卷积参数对下一个区域进行特征提取。
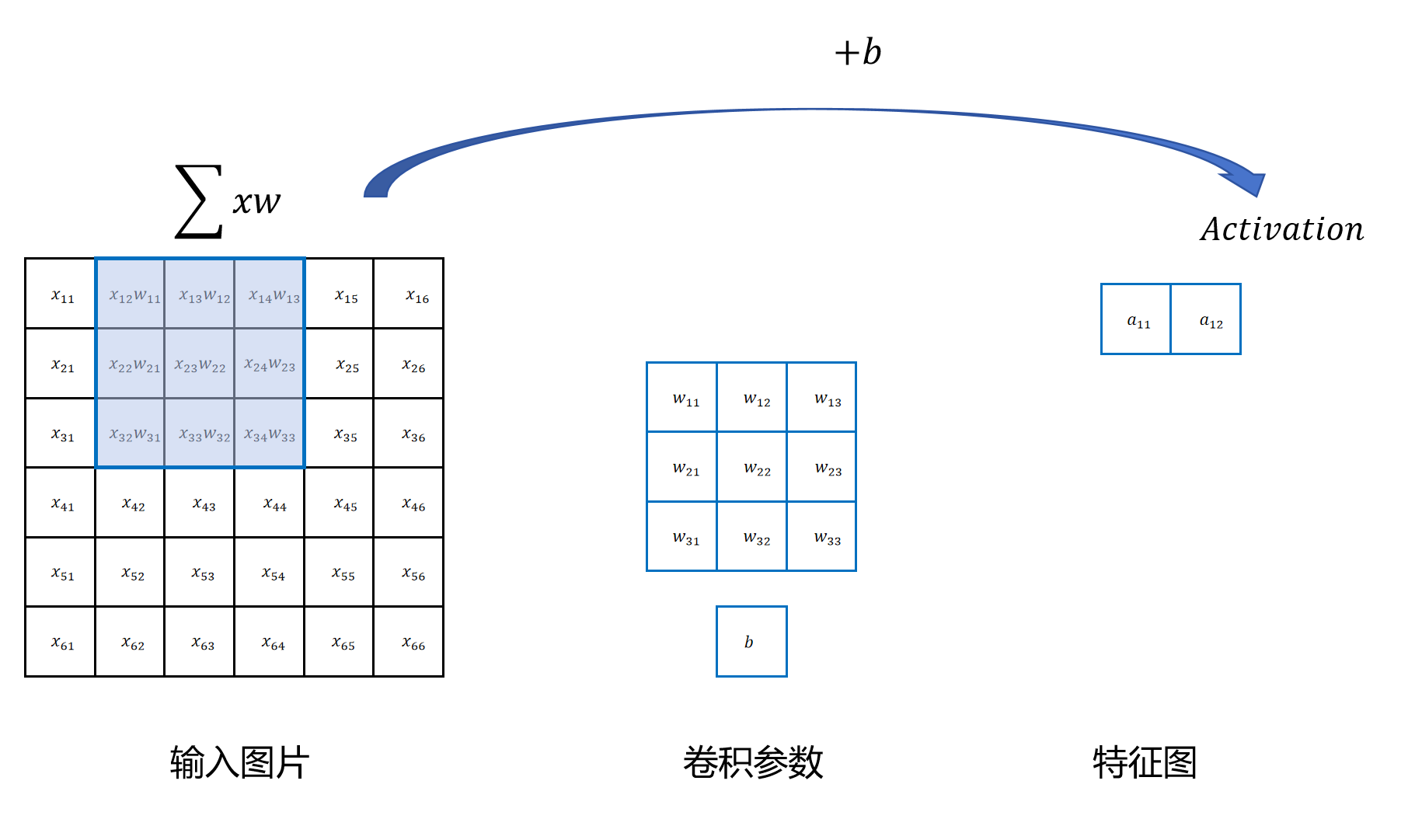
最后当完成对图片的扫描后，我们就得到一个新的完整的特征图：
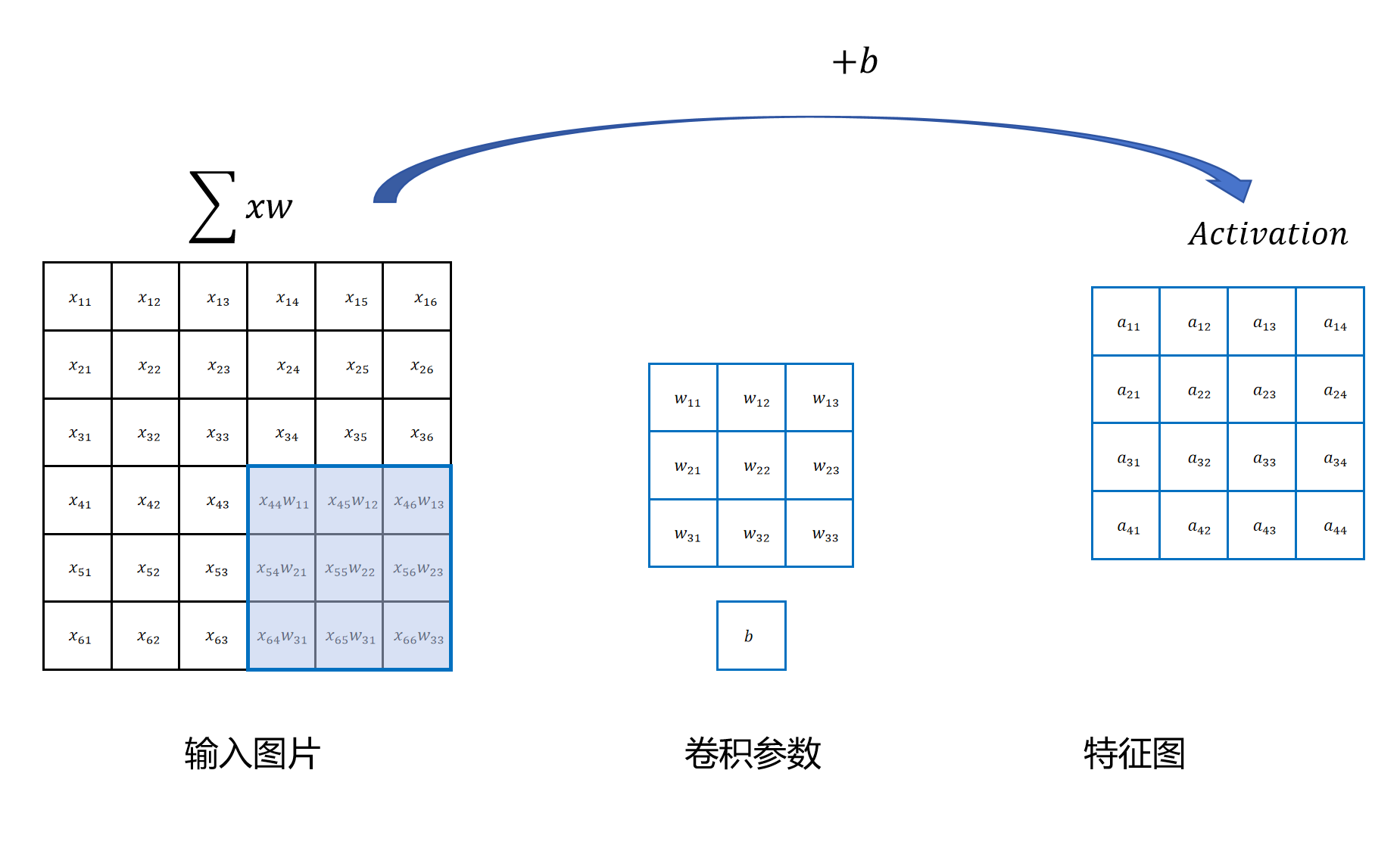
10.2.2 卷积操作的优点
卷积操作完美解决了视觉问题的三个痛点。
图片输入特征多 图片输入特征多，但是一个3x3的卷积操作只有10个参数，就可以对整个图片进行扫描。
特征局部性 卷积操作的每个运算只在特定相邻区域内进行，并不要所有输入特征都参与运算。
平移不变性 卷积操作在整个图片上进行滑动检测，就是假设图片的特征具有平移不变性。
所以对于一个3x3的卷积操作，它只用10个参数就可以在任意大的图片上提取特征。
10.2.3 卷积操作与全连接操作
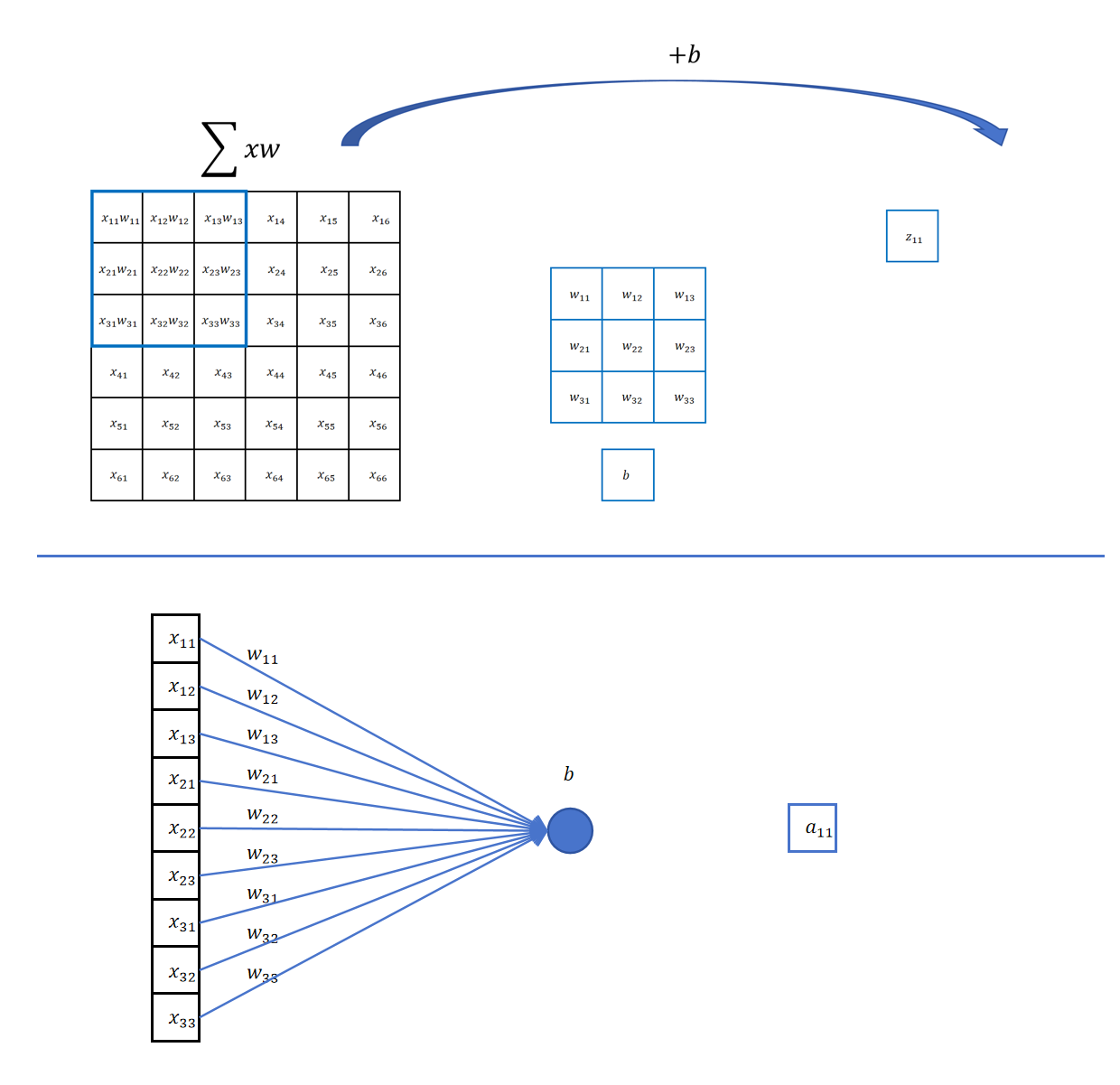
卷积操作和全连接操作并没有本质的不同。对于一个3x3的卷积操作，你可以看成是一个连接9个输入的神经元，它有9个weight参数，一个bias参数。这个神经元会用同样的参数对输入特征图上的任意3x3区域进行计算，形成输出的特征图。
所以卷积操作可看作带有先验知识（局部性、平移不变性）的参数共享全连接层。
10.2.4 多通道卷积操作
上边我们讲的是单通道的黑白照片作为输入，那么对于3通道RGB彩色图片作为输入，卷积操作会有什么不同呢？
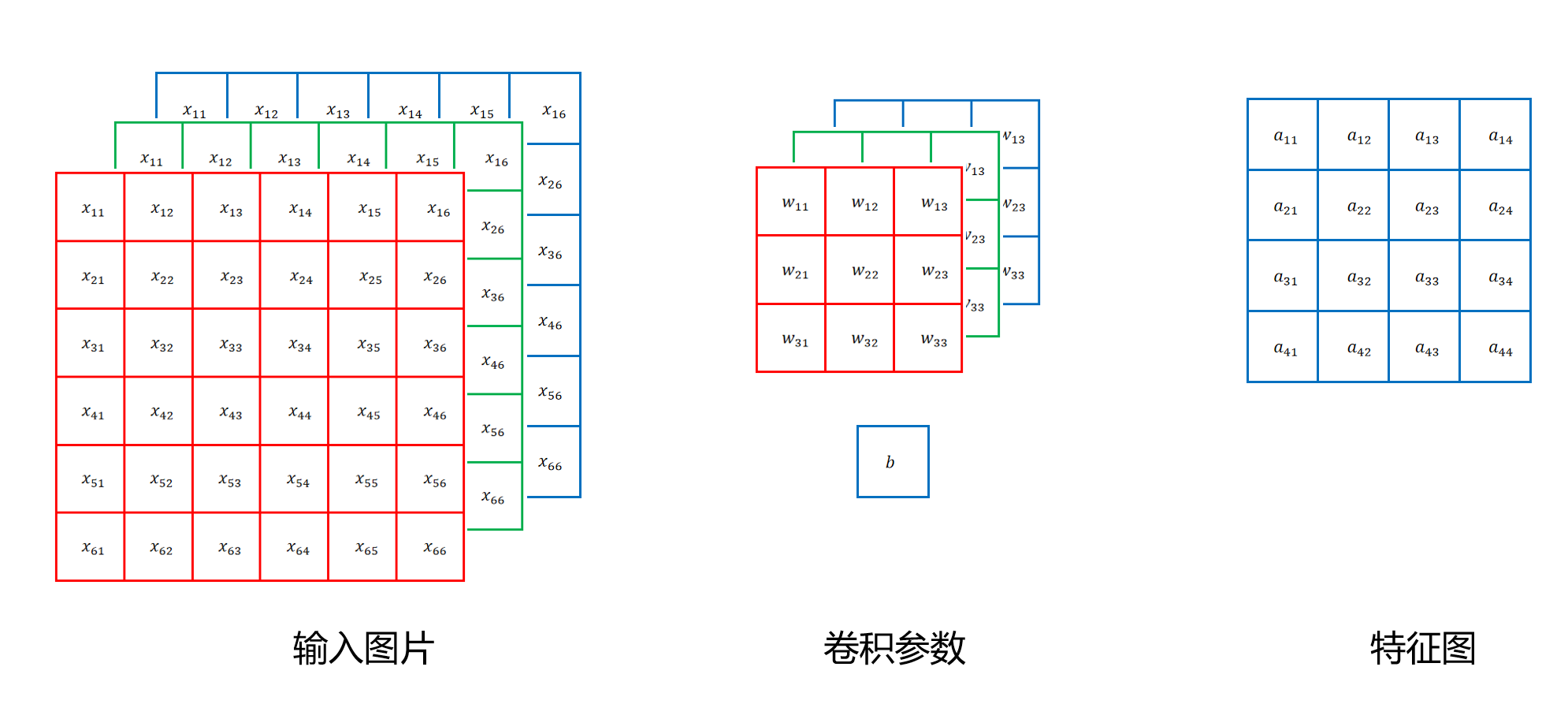
如果输入特征图是3通道的，那么卷积核也必须是3通道的，卷积核的shape为3x3x3，偏置还是只有一个参数b，一共28个参数。在进行卷积操作时，第一个通道的输入和第一个通道的卷积核参数进行卷积操作，第二个通道的输入和第二个通道的卷积核参数进行卷积操作，第三个通道也是类似，然后将三个通道得到的卷积值相加，再加上偏置值b，最终一个三通道卷积操作还是得到一个值。最终输出的通道数还是1个。换句话说，就是对应通道，对应高，对应宽位置上的输入和权重相乘，最后累加所有的值，再加上b值，经过激活函数，得到3x3x3输入区域的特征值a。
10.2.5 多Filter操作
上边我们讲过如果输入特征图是多通道的，如果通道数为C，那么卷积核的通道数也必须为C，但是输出的特征图还只是一个通道。一个卷积操作可能是检测图片里某一种特征，比如在检测猫的例子里，是检测猫的眼睛，我们还需要检测其他特征，比如猫的耳朵，猫的嘴巴等器官。那么我们在一个卷积层里可以定义多个Filter（卷积操作），当我们定义了几个Filter，输出的通道数就为几。
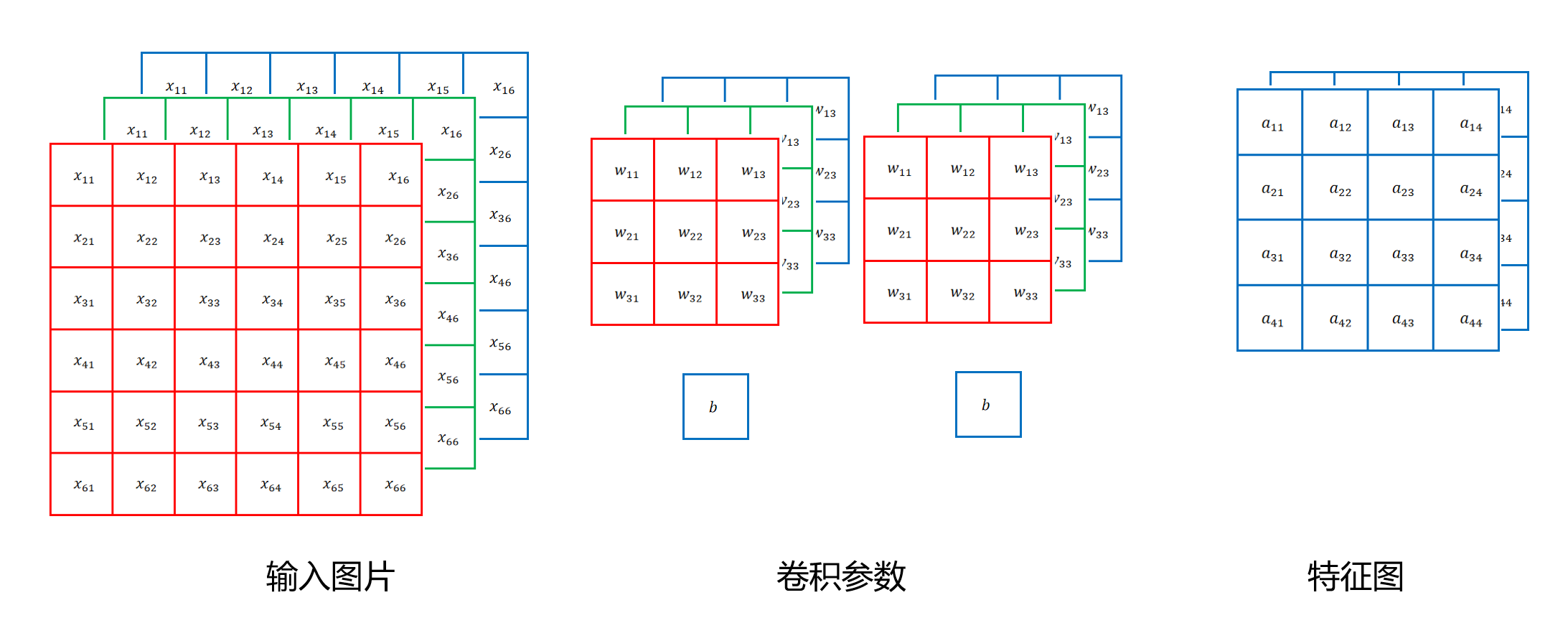
比如上图中，我们对一个输入通道为3的特征图进行卷积，定义了两个Filter，每个Filter的卷积核都是3x3x3。因为定义了2个Filter，最终得到的输出特征图的通道数为2。
10.2.6 定义多个卷积层
之前我们讲过，深度神经网络为什么效果好，是因为每一层都可以看做是一个特征提取器，浅层提取初级特征，深层在初级特征的基础上提取高级的特征。
同样卷积层也可以定义多个进行累加。因为输入的是原始的图像的RGB特征图，第一层，我们定义多个Filter，它们检测原始图像中的点、线、纹理等，生成输出的特征图。输出特征图仍然具备视觉问题的特点，即局部性和平移不变性。所以可以在输出的特征图上继续定义卷积层，也可以定义多个Filter，用来从点、线、纹理这样的基础特征上提取眼睛、鼻子、嘴巴等这样的高级特征。需要注意的是每一个卷积层上的卷积核的通道数，都必须等于它输入特征图的通道数。
所以一般在定义卷积神经网络时，会堆叠多个卷积层，每个卷积层也会定义多个Filter，来提取不同的特征。
10.2.7 卷积核工作的直观理解
假设有以下的3x3的黑白图片，其中0表示全黑，255表示全白。
可以看到上边图片中有一个明暗分隔的竖线。它的像素灰度值为：
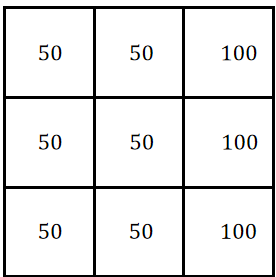
这时我们如果手动设置如下一个卷积核C1，它的权重为：
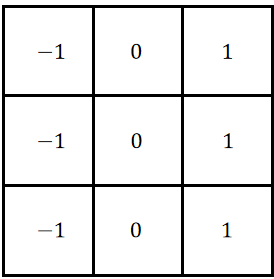那么这个C1输出的值为150。
如果我们用C1来检测一个纯色3x3方块呢？
纯色3x3的方块对应的图像和灰度值为：
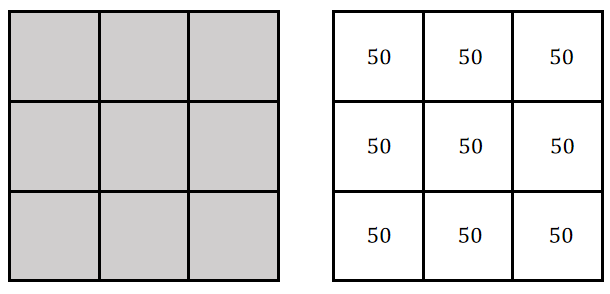经过计算你可以发现C1输出的值为0。
如果我们用C1来检测一个有着横条纹的3x3方块呢？
横条纹3x3方块对应的图像和灰度值为：
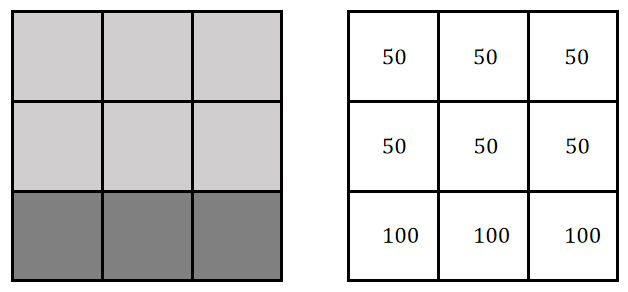经过计算，可以发现C1输出的值仍然为0。
所以C1就是一个竖条纹检测器。
同理你可以设计出横条纹检测的卷积核、斜条纹检测的卷积核。
但是需要注意的是，训练神经网络时，我们并不需要手动设计卷积核的权重，在训练过程中它会自己学到检测各种特征的卷积核。
10.2.8 PyTorch 里的特征图的表示
在我们前面的介绍中，特征图的格式是按照“高 × 宽 × 通道数”（Height × Width × Channels，HWC）来组织的。在一些深度学习框架中，比如 TensorFlow，默认也使用这种格式（channels_last）。
但是在 PyTorch 中，特征图的张量（tensor）采用的是“通道数 × 高 × 宽”（Channels × Height × Width，CHW）这种格式，也就是 channels_first。
比如，对于一张高为 224、宽为 112 的 3 通道彩色图片，在读入 PyTorch 后，它的张量形状为：[3, 224, 112]。
由于一般学术论文里默认采用HWC格式，所以本书后边都采用HWC格式。但是你在调试PyTorch代码时需要注意格式的不同。