3.5 一元函数微分

3.5.1 微分的由来

首先我们看函数：$y=f(x)=2x$，在$x_0$处有：

可以看到在$x_0$处，y的增量等于x的增量的2倍。

接着看函数：$y=x^2$, 在$x_0$处有：

可以看到在$x_0$处，y的增量由两部分构成，第一部分可以看做一个常数$2x_0$与x的增量$\triangle x$的乘积，这部分$\triangle x$和$\triangle y$满足线性关系。第二部分，当$\triangle x$趋于0时，可以看做是$\triangle x$的高阶无穷小。所以当$\triangle x$趋于0时，原本x和y不是线性关系，但是x和y的增量部分，$\triangle y$就可以用$\triangle x$线性表示。所以当$\triangle x$变化很小时，就可以用简单的线性估算出$\triangle y$。

最后我们再看一个函数：$y=x^3$, 在$x_0$处有：

当$\triangle x$趋于0时，$\triangle y$也可以由$\triangle x$的线性部分$3{x_0}^2\triangle x$和$\triangle x$的高阶无穷小部分$(\triangle x)^3$构成。

3.5.2 微分的定义

通过上边3个函数我们发现，当$\triangle x$趋于0时，$\triangle y$可以表示为一个常数A与$\triangle x$的乘积加上一个$\triangle x$的高阶无穷小。

则称$y=f(x)$在$x_0$处可微。$A \triangle x$为线性主部（线性关系的主要部分）。记作：

$\mathrm{d}x$和$\mathrm{d}y$分别是x和y的微分。

可微描述的是$\triangle x$和$\triangle y$之间的类线性关系。

3.5.3微分和导数的关系

$\mathrm{d}y = A \mathrm{d}x$ 中的A等于$f'(x_0)$。

通过3.5.1节的几个例子，你可以发现：

对于$y=2x$，A等于2。

对于$y=x^2$，A等于$2x_0$。

对于$y=x^3$，A等于$3(x_0)^2$。

A都等于在$x_0$处的导数。

下边给出证明：

根据微分定义

$\triangle y = A \triangle x + O(\triangle x);(\triangle x \to 0)$

则有：

所以$f'(x_0)=A$

在一元函数里，可微和可导是等价的。可微必可导，可导必可微。

3.5.4微分的几何意义

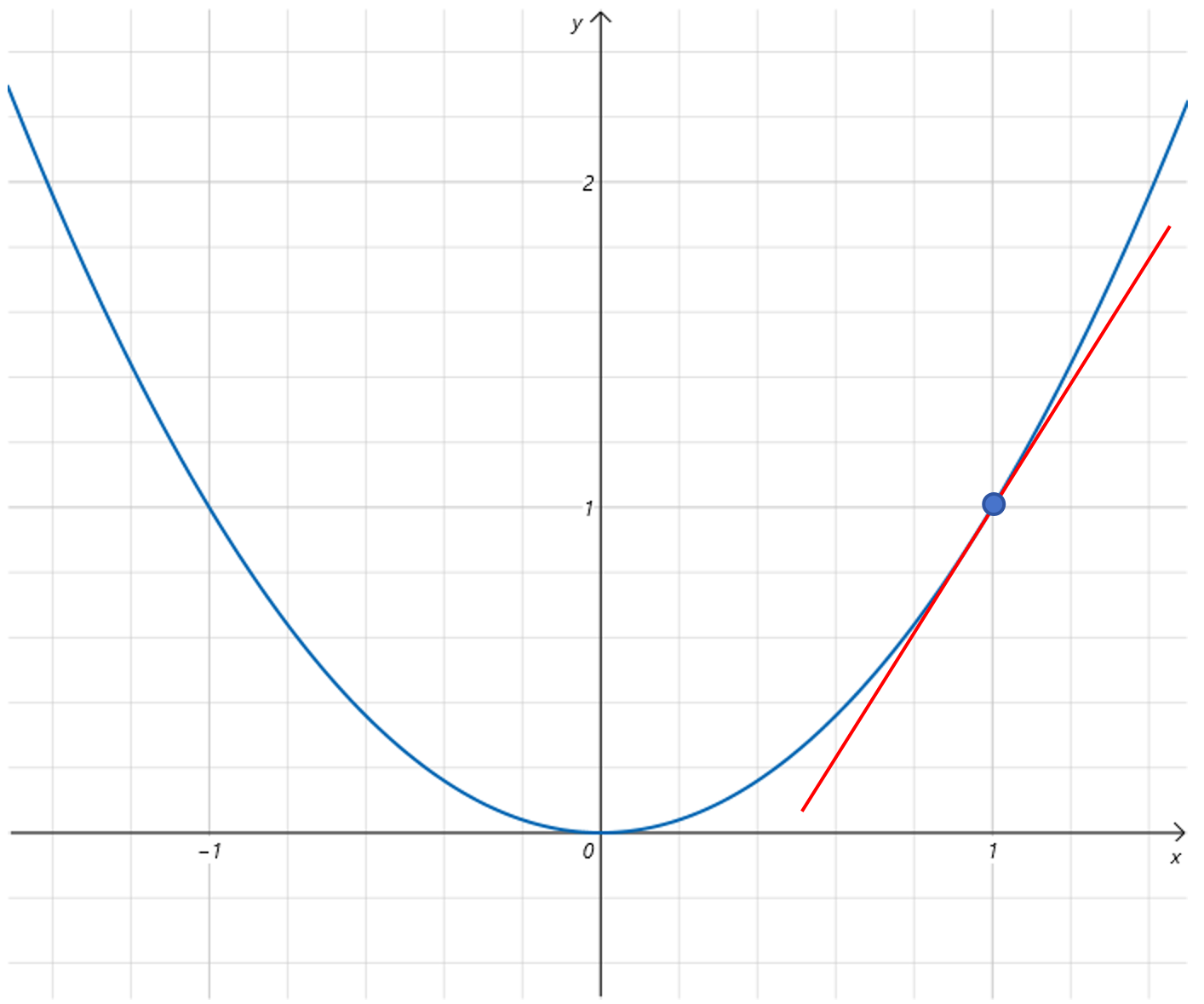
微分的几何意义就是以直代曲。用直线代替曲线。比如上图中$y=x^2$当x等于1附近，x发生微小变化时，y的变化可以用$\mathrm{d}y = 2 \mathrm{d}x$这个线性变化来近似。