2.4 向量点乘

2.4.1 物理里的功

首先我们复习一下物理里对功的定义。

如果一个物体受到力的作用，并在力的方向上发生了一段位移，我们就说这个力对物体做了功。功是物理学中表示力对位移的累积的物理量。功是标量，没有方向的概念。

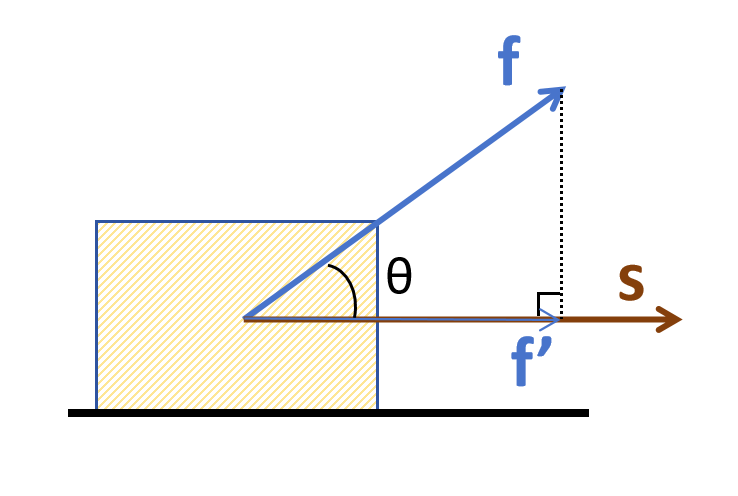
上图中里的力f和位移s都是向量，它们都既有大小，又有方向，并且它们两个的方向并不相同。这时，计算功时，需要考虑将f投影到s上，得到f'，然后用f'的模长乘以s的模长就是功，用公式表示如下：

$W= |f|\times cos\theta \times |s|$

2.4.2 点乘的定义

上边对功的计算得到的结果是一个标量，它等于两个向量的模长与它们之间夹角cos值的乘积。

这实际上就是向量点乘（或者叫做点积、数量积）的定义。用符号 $\cdot$表示。所以功的定义可以用点积形式表示如下：

$W=f \cdot s= |f||s| cos\theta$

上边在对功的计算中是将力f投影到位移s上，实际上通过观察公式我们可以发现，两个向量是对称的，也就是说将s投影到f上的向量s'的模长乘以f的模长也可以得到一样的结果。总之，点积就是两个向量模长与它们夹角余弦值的乘积。

下边给出线性代数里点乘正式的定义，两个向量a和b。它们在同一个向量空间，也就说它们的分量个数相同。它们两个的点乘为：

$a \cdot b = |a||b|cos\theta$

2.4.3 点乘的计算

我们知道了点乘的定义，它等于两个向量的模长与它们之间夹角余弦值的乘积。但是这里又有模长，又有cos，都不好计算。实际上点乘的计算非常简单。我们就根据点乘的定义，一起来推导一下点乘的计算公式。首先看几个点乘的运算法则。

交换律

上边我们讲到过，根据点乘的定义，可以看到，两个向量是对称的，所以满足交换律。

$a \cdot b = b \cdot a$

数乘结合率

$(\lambda a) \cdot b=a \cdot ( \lambda b)= \lambda (a \cdot b)$

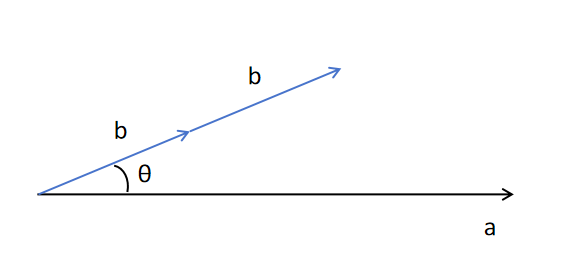
根据上边这张图，可以帮助你理解。对于$a \cdot b$ 的结果等于a的模长乘以b的模长再乘以cosθ。当b变为原来的 λ倍后，它的模长变为原来的 λ倍，而a的模长和cosθ都不变，所以$a \cdot (\lambda b) = \lambda (a \cdot b) = (\lambda a) \cdot b$

分配率 点乘的分配率公式为：

$(a+b) \cdot c=a \cdot c + b\cdot c$

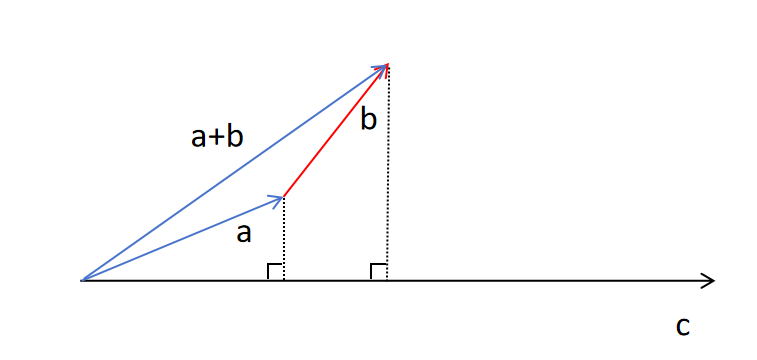上边的图可以帮助你理解，对于a+b与c的点乘，等于a+b在c上的投影的模长，乘以c的模长。而a+b在c上的投影的模长就等于a在c上投影的模长加上b在c上投影的模长。而a在c上投影的模长乘以c的模长就是a与c的点乘，对于b也同理。所以上式成立。

有了以上几个向量点乘的计算法则，我们就可以来推导点乘的计算公式了。

以三维向量$a \cdot b$为例： 将向量a，b用标准基向量i,j,k表示。比如对于a来说，它在x，y，z轴的分量分别为$a_x,a_y,a_z$,则：

$a \cdot b = (a_xi+a_yj+a_zk) \cdot (b_xi+b_yj+b_zk)$

根据分配率和数乘结合律有：

$a \cdot b = a_xb_x(i \cdot i)+a_xb_y(i \cdot j)+a_xb_z(i \cdot k)+a_yb_x(j \cdot i)+a_yb_y(j \cdot j)+a_yb_z(j \cdot k)$

$+a_zb_x(k \cdot i)+a_zb_y(k \cdot j)+a_zb_z(k \cdot k)$

上式中$a_x,a_y,a_z,b_x,b_y,b_z$都为标量，$i,j,k$为标准基向量。 接下来我们计算上式中括号内的标准基向量之间的点乘。因为标准基向量的模长为1，又加之它们与自身夹角为0度，cos值为1，所以它们与自身的点乘为1。即：

$i \cdot i = 1$

$j \cdot j = 1$

$k \cdot k = 1$

又因为标准基向量之间都互相垂直，cos值为0，所以只要是不同标准基向量的点乘都为0。即：

$i \cdot j = 0$

$i \cdot k = 0$

$j \cdot k = 0$

带入上边式中有：

$a \cdot b = a_xb_x+a_yb_y+a_zb_z$

可以看到点乘有一个非常简单的计算规则，就是两个向量的点乘等于两个向量各个分量的值相乘再加和，这个规则可以推广到任意维度的向量点乘上,即：

$a \cdot b = \sum_{i=1}^{n}a_ib_i$

2.4.4 点乘的作用

在深度学习里，经常用两个向量之间的夹角的余弦值来表示两个向量的相似度。比如在深度学习里，模型学习到的人脸特征都是用向量来表示，最终如何判断两个人脸向量是否代表同一个人，就是通过计算这两个向量之间的余弦值来判断。如果余弦值接近1。也就是两个向量之间夹角接近0，则认为这两个向量相似，也就是两个人脸照片相似。这里就用到了点乘。

$cos\theta = \frac{a \cdot b}{ |a||b|}$

很多情况下都会把特征向量归一化到模长为1，也就是|a||b|都为1。

两个向量的相似性计算就变为：

$CosSimilarity= a \cdot b$

所以最终变化为，计算两个向量之间的点乘，就是计算两个向量的相似度。

为什么深度学习会用Cos相似度来衡量向量之间的相似性呢？而不用欧式距离呢？

一是因为点乘计算简单，效率高。

二是不同维度向量之间的Cos相似度有可比性，比如两个向量方向完全一样，值就是1; 两个向量垂直，也就是完全无关，值为0；两个向量方向相反，也就是负相关，值为-1。但是欧式距离不同维度向量之间的距离可能相差很远，没有可比性。