17.2 旋转位置编码

之前我们讲过Transformer里使用sin和cos函数生成位置编码，Bert里采用的是可学习位置编码，Llama-1采用了旋转位置编码。在大模型时代越来越多的模型采用了旋转位置编码，今天我们就来一探究竟。

17.2.1 旋转矩阵

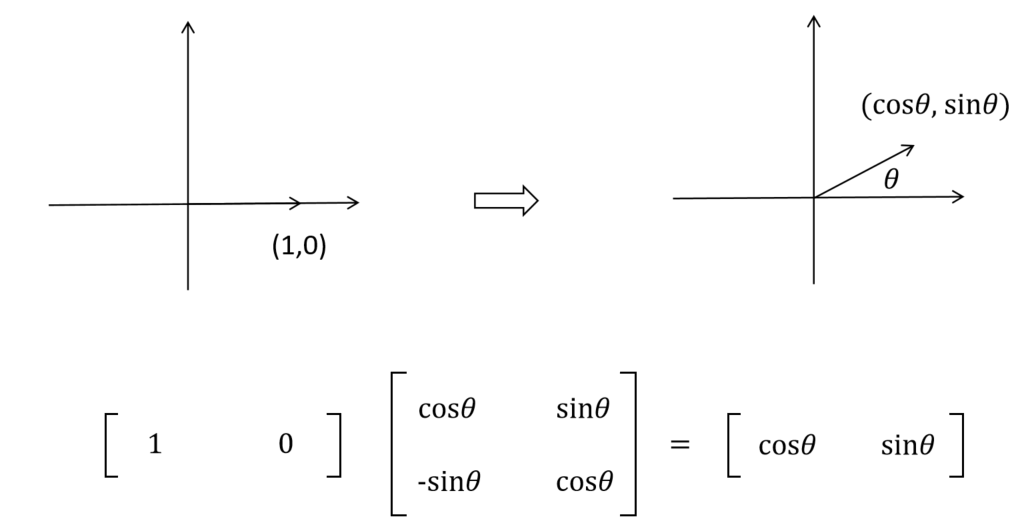
旋转位置编码的核心是通过sin和cos函数构成的旋转矩阵，对二维向量进行旋转。在二维坐标系里，假设一个向量位于x轴上，即向量$v=(1,0)$。我们希望讲这个向量绕原点旋转一个角度$\theta$。旋转后的向量$v'$长度保持不变，则其坐标变化为$(cos\theta,sin\theta)$。我们定义旋转矩阵$R(\theta)$为：

$R(\theta)=\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$

将向量$v$与旋转矩阵$R(\theta)$相乘后，结果为$(cos\theta,sin\theta)$。

同理，对于位于y轴上的向量$v=(0,1)$，逆时针旋转$\theta$后，得到向量$v'=(-sin\theta,cos\theta)$。$v'$同样等于$v$与旋转矩阵$R(\theta)$相乘的结果。

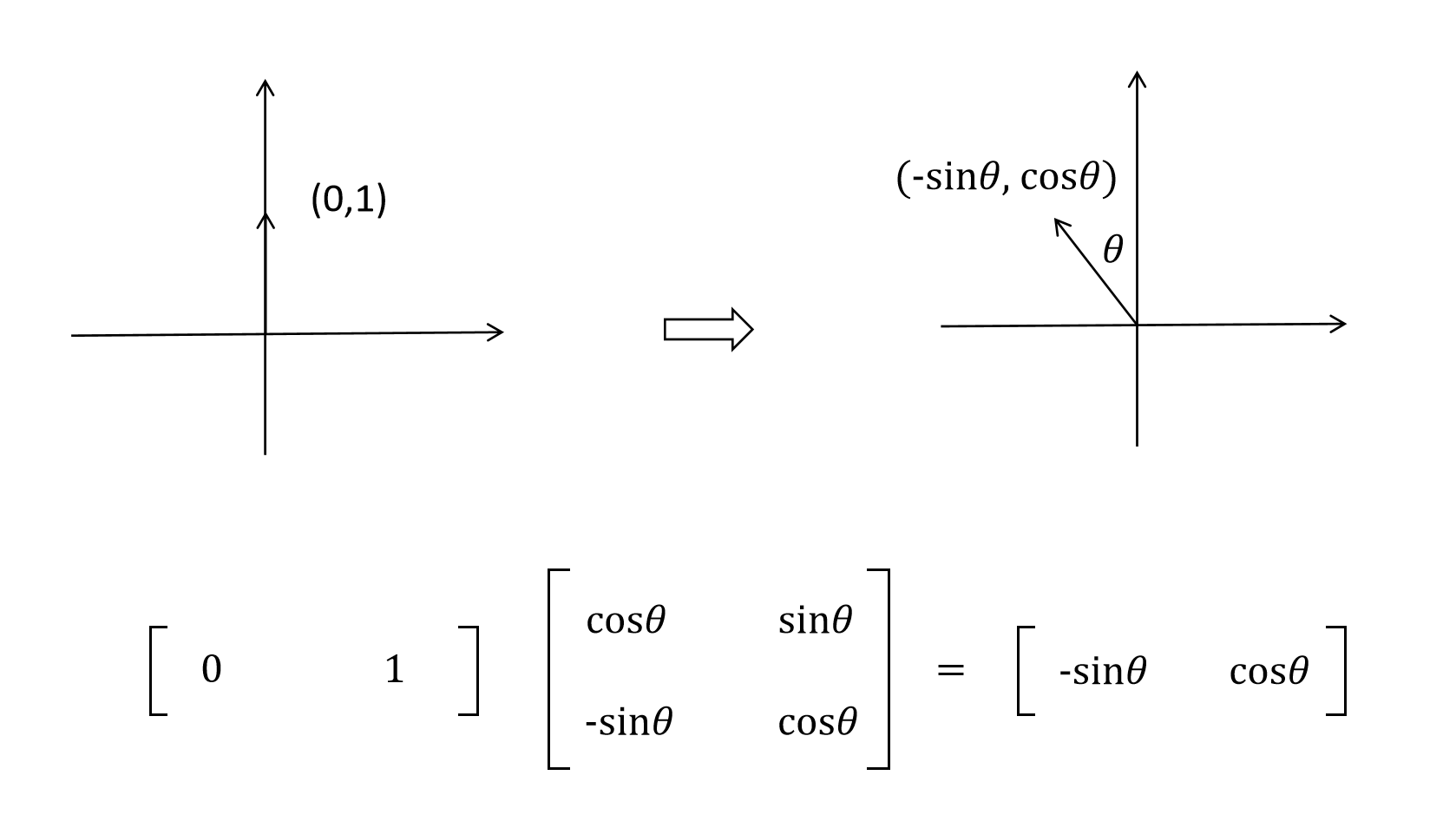
向量（1,0）和向量（0,1）是二维坐标系中的标准基向量。当这两个基向量通过旋转矩阵$R(\theta)$逆时针旋转$\theta$角度时，则等于整个坐标系随之旋转了$\theta$角度。

接下来证明一下旋转矩阵$R(\theta)$可以对任意二维向量进行逆时针旋转$\theta$角度。假设一个向量长度为$r$,与x轴夹角为$\alpha$，逆时针旋转$\beta$角度。则证明如下：

$\begin{bmatrix} rcos\alpha& rsin\alpha \end{bmatrix} \begin{bmatrix} cos\beta & sin\beta \\ -sin\beta & cos\beta \end{bmatrix}$

$=\begin{bmatrix} rcos\theta*cos\beta-rsin\alpha * sin\beta & rcos\alpha * sin\beta+rsin\alpha*cos\beta \end{bmatrix}$

$\begin{bmatrix} rcos(\alpha+\beta)& rsin(\alpha+\beta) \end{bmatrix}$

17.2.2 旋转矩阵的性质

旋转矩阵具备以下两个性质： 旋转矩阵具有结合性：

$R(\theta_1)R(\theta_2)=R(\theta_1+\theta_2)$

旋转矩阵的转置就是旋转负的$\theta$角度，证明如下：

$R(\theta)^{T}=\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}=\begin{bmatrix} cos(-\theta) & sin(-\theta) \\ -sin(-\theta) & cos(-\theta) \end{bmatrix}=R(-\theta)$

其中证明过程中用到了sin和cos的奇偶性：$cos\theta=cos(-\theta)$和$sin(-\theta)=-sin\theta$

17.2.3 旋转位置编码

在Transformer架构里进行注意力计算时，关键在于计算查询向量q和应答向量k之间的点积。$qk^T$表示两个向量之间的点积，这种计算方式没有直接考虑到token的位置信息。为了引入位置信息，可以通过旋转矩阵对两个向量进行编码来添加位置信息。编码过程为对每个向量根据它们的位置索引（分别为m和n）进行旋转。如果对q应用旋转矩阵$R(m)$，对k应用旋转矩阵$R(n)$，然后再进行点积计算，则有：

$qR(m)\cdot kR(n)$

$=qR(m)R(n)^Tk^T$

$=qR(m)R(-n)k^T$

$=qR(m-n)k^T$

上边的证明用到了旋转矩阵的两个性质。我们注意到最后得到的注意力表达式里不光含有q，k，还还有m-n这样的相对位置信息。这种相对位置信息可以更好的建模token之间的关系。

17.2.4 拓展到高维

上边讨论的是2维的旋转矩阵，如何扩展到高维呢？答案是将维度两两一组进行旋转，如果q和k的特征长度为8，那么就让特征两两一组，一共4组。每一组在它们两个特征组成的子空间内进行旋转，至于是哪两个特征一组，是无所谓的。任意两个一组都可以。

如下图所示，m代表token的位置，比如一个token在序列里第一个，m就为0。F代表sin()和cos()的系数。在这个公式里，系数最大的是第一个二维子空间，系数为1。系数最大，则波长最短。同理，系数最小的是最后一个二维子空间，系数接近1/10000。系数最小，波长最长。

给予不同的二维子空间不同的旋转频率，是因为sin()和cos()都是周期函数。可以通过时钟来理解，频率最快的是秒针，它精准，但是每过一分钟就重复一次。频率最慢的是时针，它频率慢，但不容易重复。秒针，分针和时针一起组合来构成时间。

因为多维旋转矩阵里大部分都是0，token的特征在和多维旋转矩阵相乘时可以简化，其中h是token的特征向量，$h_i$是特征向量第i个位置的值。$R(h,m)$表示对序列里第m个位置的token的特征向量h进行旋转。

$R(h,m)_1=[h_0,h_1,...h_{d-2},h_{d-1}]\otimes [cos(mf_0),cos(mf_0),..,cos(mf_{\frac{d}{2}-1}),cos(mf_{\frac{d}{2}-1})]$

$R(h,m)_2=[-h_1,h_0,...-h_{d-1},h_{d-2}]\otimes [sin(mf_0),sin(mf_0),..,sin(mf_{\frac{d}{2}-1}),sin(mf_{\frac{d}{2}-1})]$

$R(h,m)=R(h,m)_1+R(h,m)_2$