8.5神经网络的多分类

之前我们在讲逻辑回归时谈到过，可以通过一对多的方式用逻辑回归进行多分类。那样做很麻烦，要训练多个模型，而且最后无法给出预测样本属于每一个类别的概率值。神经网络对于多分类有更好的解决办法。

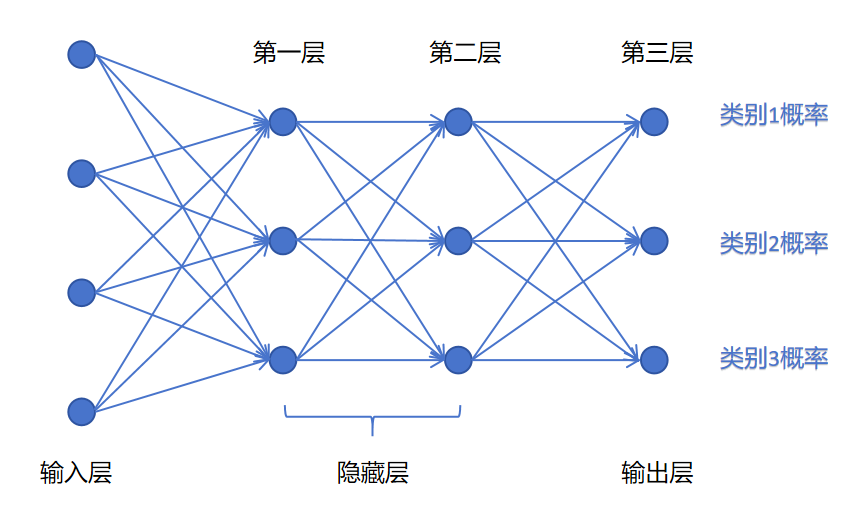
假如我们的神经网络需要进行三分类，那么我们可以设置输出层的神经元个数为3个。并且希望每个输出神经元可以输出一个类别的概率，表明这个样本属于这个类别的概率。

对于神经网络，输出层经过线性回归，还没有经过激活函数的值，叫做logits。logits经过激活函数后就是最终的输出值了。

我们希望神经网络最后一层的logtis经过激活函数后可以代表样本属于每个类别的概率值。既然是概率值，则要求它们的和为1。

你可能有一个直接的想法，那就是用每个神经元logits的值，除以所有神经元logits值的和作为最终的概率值。这样做有两个问题： 1. logits的值有正有负，这样得到每个神经元的激活值，也就是概率值可能为负。 2. 这样做对不同类别的差异是线性的，我们希望能放大不同类别的差异，加速训练过程。

所以，人们提出了softmax函数。我们假设输出层3个神经元的logits值为 $z_1,z_2,z_3$ ，经过softmax输出的概率值为 $o_1,o_2,o_3$ ，softmax函数的计算公式如下：

$o_1 = \frac{e^{z_1}}{e^{z_1}+e^{z_2}+e^{z_3}}$

$o_2 = \frac{e^{z_2}}{e^{z_1}+e^{z_2}+e^{z_3}}$

$o_3 = \frac{e^{z_3}}{e^{z_1}+e^{z_2}+e^{z_3}}$

然后我们给出通用的softmax的公式：假设这个分类问题有n个类别，也就是输出层有n个神经元，输出的logits值有n个。对于第i个logits值输出的概率值，通过softmax计算公式如下：

$o_i = \frac{e^{z_i}}{e^{z_1}+e^{z_2}+\cdot\cdot\cdot+e^{z_n}}$

然后我们看一下softmax函数的优势：

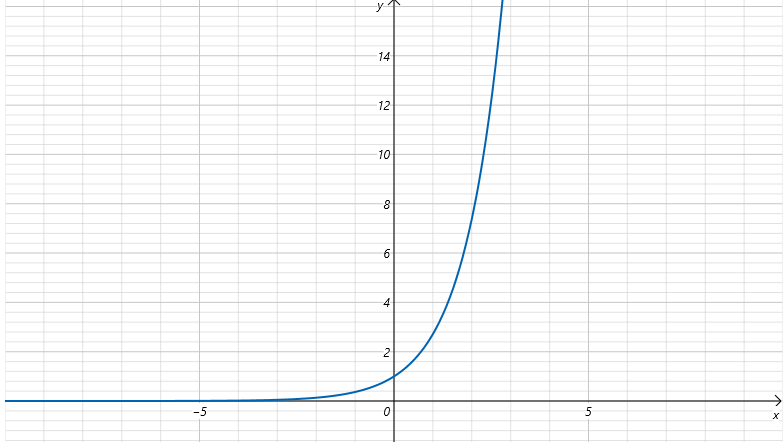
上边是 $y=e^x$ 的函数图形，可以看到不论x取值是多少，经过 $e^x$ 之后，输出值都是大于0的。解决了我们之前说的取值有正有负的问题。保证了输出概率值都为正，且在0-1之间。

另外softmax可以放大logtis之间的差异，加快训练速度。比如logits值为[2,2,5]，普通归一化后的值为：[0.22, 0.22, 0.56]，softmax之后为：[0.0453, 0.0453, 0.9094]。

之前我们讲过逻辑回归的损失函数，它是针对二分类的。对于多分类问题，同样使用交叉熵损失函数。假设如下：

类别个数为C。
真实标签用one-hot向量表示： $y=(y_1,y_2,\cdot\cdot\cdot,y_C)$ 其中y是一个样本的标签值，它的值是一个向量，有C个元素，里边只有一个元素 $y_i=1$ ，代表这个样本的真实类别，其余值都为0。
预测的概率分布是： $p=(p_1,p_2,\cdot\cdot\cdot,p_C)$ 其中p是这个样本经过神经网络的softmax激活输出，它的值是一个向量，有C个元素，这C个元素因为是softmax的输出，代表概率，满足 $\sum_{i=1}^{C}p_i=1$ 。

那么交叉熵损失定义为：

$loss = -\sum_{i=1}^{C}y_ilog(p_i)$

对于一个具体的样本，由于 $y_i$ 只有一个为1，其余都为0，所以上式可以简化为：

$loss=-log(p_y)$

其中 $p_y$ 是模型对真实类别y的预测概率。如果样本的真实类别为2，则这个样本的损失值就为 $loss=-log(p_2)$ ，当 $p_2$ 等于1时（预测类别和真实类别一致），loss为0。当 $p_2$ 越接近0，loss越接近无穷大。

如果是对于批量样本计算loss，batch size 是N，则总的交叉熵损失就为：

$loss = -\frac{1}{N}\sum_{n=1}^{N}\sum_{i=1}^{C}y_i^nlog(p_i^n)$

对于二分类问题，也可以让神经网络最后输出层有2个神经元，输出2个logtis，利用softmax做二分类。但是更常用的方式还是让神经网络最后输出一个值，用sigmoid函数转化为0-1之间的概率，用1表示正例，0表示负例。

神经网络的多分类