6.7优美的loss曲线

在模型训练过程中，有一个最重要的指标，就是loss值。而通过观察loss值变化的曲线，可以得到很多有用的信息。首先，我们利用TensorBoard这个工具来对上一节我们实现的线性回归模型训练过程绘制loss曲线。

6.7.1安装TensorBoard库

你可以通过下边的命令来安装TensorBoard库。

1. 打开Anaconda Prompt。
2. 通过conda activate 切换到你的conda环境。
3. pip install tensorboard

6.7.2修改代码

import torch
from torch.utils.tensorboard import SummaryWriter

# 确保CUDA可用
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 生成数据
inputs = torch.rand(100, 3)  # 生成shape为(100,3)的tensor，里边每个元素的值都是0-1之间
weights = torch.tensor([[1.1], [2.2], [3.3]])
bias = torch.tensor(4.4)
targets = inputs @ weights + bias + 0.1 * torch.randn(100, 1)  # 增加一些随机，模拟真实情况

# 创建一个SummaryWriter实例
writer = SummaryWriter(log_dir="runs/lr")

# 初始化参数时直接放在CUDA上，并启用梯度追踪
w = torch.rand(3, 1, requires_grad=True, device=device)
b = torch.rand(1, requires_grad=True, device=device)

# 将数据移至相同设备
inputs = inputs.to(device)
targets = targets.to(device)

epoch = 10000
lr = 0.003

for i in range(epoch):
    outputs = inputs @ w + b
    loss = torch.mean(torch.square(outputs - targets))
    print("loss:", loss.item())
    #记录loss，三个参数分别：tag，loss值，第几步
    writer.add_scalar("loss/train", loss.item(), i)
    loss.backward()

    with torch.no_grad():  # 下边的计算不需要跟踪梯度
        w -= lr * w.grad
        b -= lr * b.grad

    # 清零梯度
    w.grad.zero_()
    b.grad.zero_()

print("训练后的权重 w:", w)
print("训练后的偏置 b:", b)

在上一节的代码基础上增加了3行代码。分别是：

导入SummaryWriter类：

from torch.utils.tensorboard import SummaryWriter

创建一个SummaryWriter实例：

writer = SummaryWriter(log_dir="runs/lr")

通过log_dir设置记录文件的位置。

训练的每一步写入loss值：

writer.add_scalar("loss/train", loss.item(), i)

其中传入的3个参数分别为：标签名，loss值，训练的步数。

然后我们重新训练模型，会发现我们指定的记录位置处产生了文件。

6.7.3查看loss曲线

然后我们在Anaconda Prompt里，激活你的环境，运行下边的命令：

tensorboard --logdir=C:/projects/lr/runs/lr

注意需要设置logdir到你代码里设置的存放记录的路径。

然后你可以在浏览器里输入http://localhost:6006 来打开TensorBoard，查看loss曲线了。

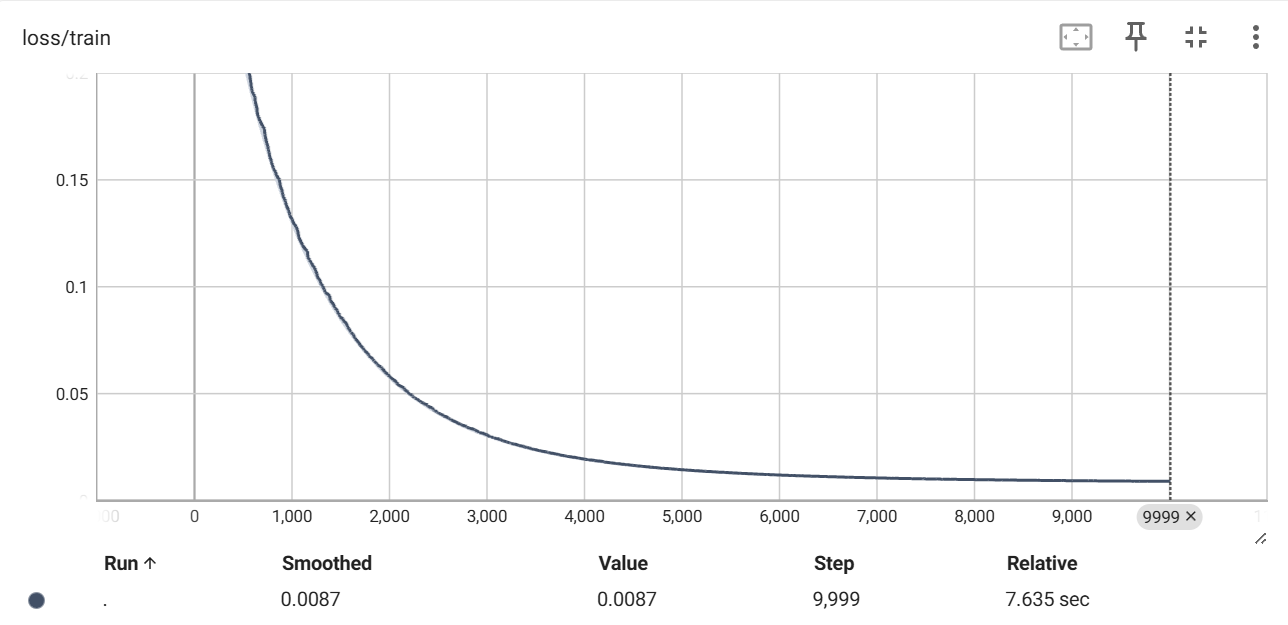
这是一个非常理想的loss曲线，前边一段训练过程loss快速下降，到后边loss逐渐变化很小，证明已经收敛。整个训练过程loss变化也很平稳，因为整个曲线很平滑。

6.7.4利用loss曲线进行诊断

上边的loss曲线很完美，但是情况并不总是如此。如果你发现你的loss曲线并不下降，那么有以下几种可能。1.你的代码有bug，你需要检查你的代码。2. 你的学习率设置太大。你可以先将学习率设置成足够小的值，然后看loss值是否下降。如果loss值还是不下降，那么很大可能就是代码的问题了。

根据loss曲线，你也可以判断什么时候终止训练，那就是loss几乎不变，看起来是一条平行于x轴的直线。这时我们认为模型收敛了，梯度下降已经不能进一步减少损失了。此时，我们就得到了最优的模型。