8.3神经网络与矩阵计算

神经网络之所以能够独步天下，成为当今最重要的机器学习算法。与它可以将计算转化为高效的矩阵计算密不可分。再加上GPU硬件专门针对矩阵运算进行了优化。让神经网络的训练速度大幅提高，也加快了神经网络的推广。

8.3.1 一个例子

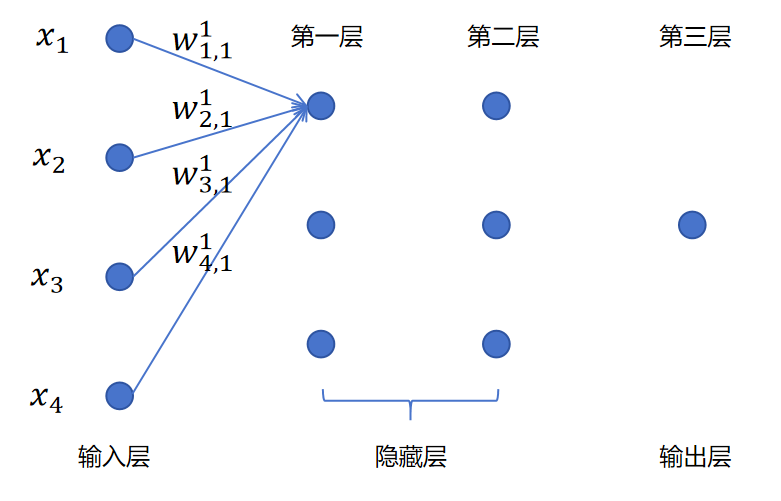
对上图这样一个3层的神经网络。我们关注第一层的第一个神经元的计算。其中x1,x2,x3,x4x_1,x_2,x_3,x_4是一个样本的4个特征值，也就是输入层的输入。 其中w1,11w_{1,1}^1表示一个权重值。上标1，表示这是第一层的参数。下标(1,1)，第一个1表示这是针对第一个输入的权重。第二个1表示这是第一层的第1个神经元。所以w1,11w_{1,1}^1表示第一层的第一个神经元对对一个输入的权重参数。

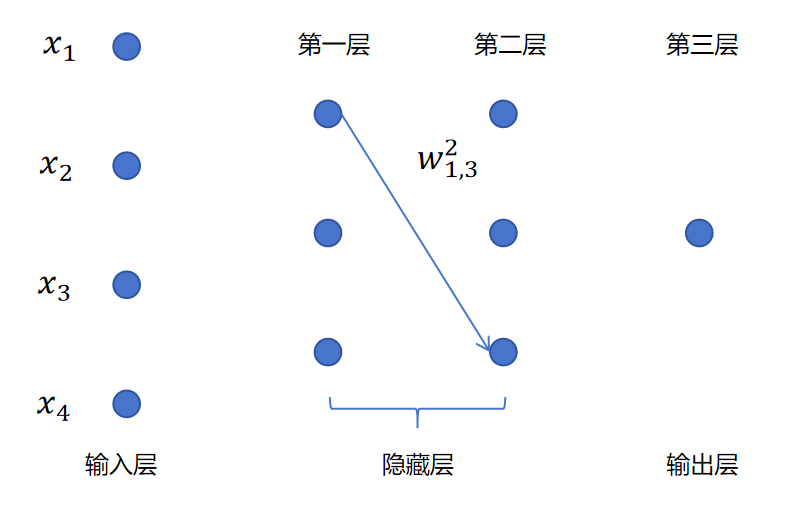
类似的对于w1,32w_{1,3}^2，就表示第2层的第3个神经元对第1个输入的权重参数。如下图所示：

我们回到第一层第一个神经元的线性回归计算，暂时不考虑偏置和激活函数。则它的计算式为：

z11=[x1,x2,x3,x4][w1,11w2,11w3,11w4,11]z_1^1=[x_1,x_2,x_3,x_4]\begin{bmatrix}w_{1,1}^1\\w_{2,1}^1\\w_{3,1}^1\\w_{4,1}^1\end{bmatrix}
其中z11z_1^1表示线性回归的结果，上标1表示第1层，下标1表示第一个神经元。

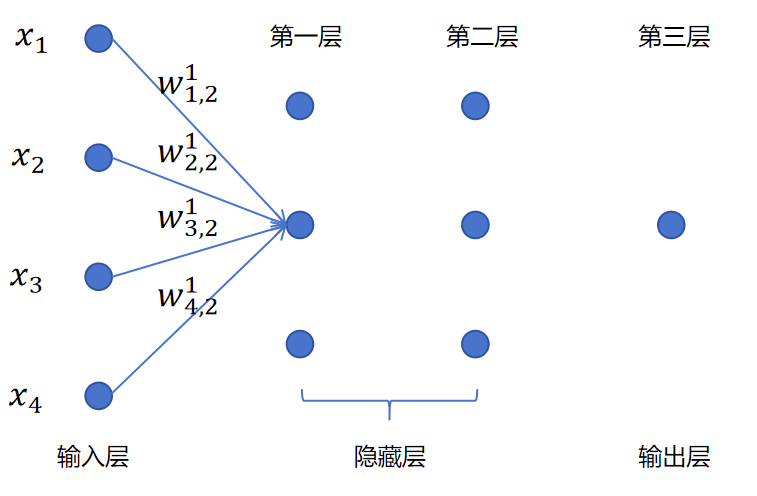
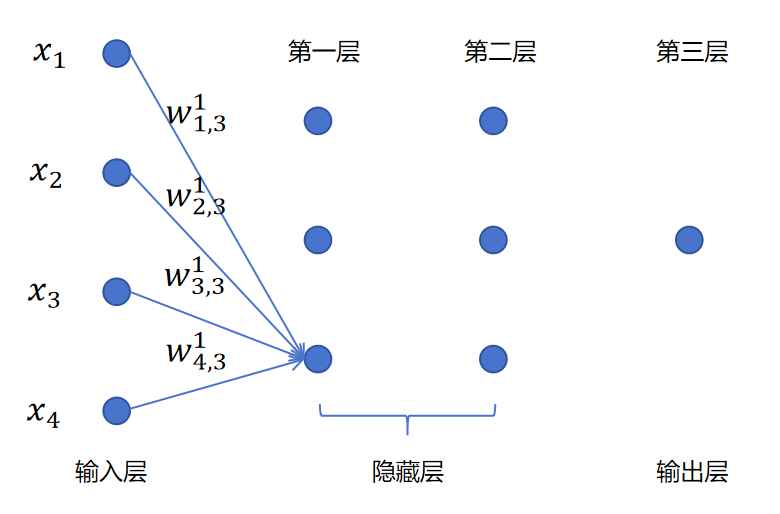
同理，我们可以得到：

z21=[x1,x2,x3,x4][w1,21w2,21w3,21w4,21]z_2^1=[x_1,x_2,x_3,x_4]\begin{bmatrix}w_{1,2}^1\\w_{2,2}^1\\w_{3,2}^1\\w_{4,2}^1\end{bmatrix}
z31=[x1,x2,x3,x4][w1,31w2,31w3,31w4,31]z_3^1=[x_1,x_2,x_3,x_4]\begin{bmatrix}w_{1,3}^1\\w_{2,3}^1\\w_{3,3}^1\\w_{4,3}^1\end{bmatrix}

上边是分别对z11,z21,z31z_1^1,z_2^1,z_3^1进行计算。我们可以换成更高效的矩阵计算方式，对z1z^1一次性进行计算。

z1=[z11,z21,z31]=[x1,x2,x3,x4][w1,11w1,21w1,31w2,11w2,21w2,31w3,11w3,21w3,31w4,11w4,21w4,31]z^1=[z_1^1,z_2^1,z_3^1]=[x_1,x_2,x_3,x_4]\begin{bmatrix}w_{1,1}^1&w_{1,2}^1&w_{1,3}^1\\w_{2,1}^1&w_{2,2}^1&w_{2,3}^1\\w_{3,1}^1&w_{3,2}^1&w_{3,3}^1\\w_{4,1}^1&w_{4,2}^1&w_{4,3}^1\end{bmatrix}

这是对一个样本的4个特征进行计算，我们可以对多个样本进行计算，这样就变成两个矩阵相乘。 x1,2x_{1,2}表示第1个样本的第2个特征。

[x11x12x13x14x21x22x23x24][w1,11w1,21w1,31w2,11w2,21w2,31w3,11w3,21w3,31w4,11w4,21w4,31]\begin{bmatrix}x_{11}&x_{12}&x_{13}&x_{14}\\x_{21}&x_{22}&x_{23}&x_{24}\end{bmatrix}\begin{bmatrix}w_{1,1}^1&w_{1,2}^1&w_{1,3}^1\\w_{2,1}^1&w_{2,2}^1&w_{2,3}^1\\w_{3,1}^1&w_{3,2}^1&w_{3,3}^1\\w_{4,1}^1&w_{4,2}^1&w_{4,3}^1\end{bmatrix}

对于每一层都是类似的，我们可以对批量输入数据和多个神经元的线性回归进行矩阵运算。这大大加速了神经网络的计算，特别是在GPU上。

当我们计算出了z1=[z11,z21,z31]z^1=[z_1^1,z_2^1,z_3^1]可以给线性回归结果加上偏置值[b11,b21,b31][b_1^1,b_2^1,b_3^1]。b21b_2^1表示第一层第二个神经元的偏置值。

z1=[z11,z21,z31]+[b11,b21,b31]z^1=[z_1^1,z_2^1,z_3^1]+[b_1^1,b_2^1,b_3^1]

然后对每个元素应用sigmoid函数就得到了第1层的激活值：

a1=sigmoid([z11,z21,z31])a^1=sigmoid([z_1^1,z_2^1,z_3^1])

接下来a1a_1就成为神经网络第二层的输入，同样第二层的计算也可以用矩阵运算完成。比如：

z2=[z12,z22,z32]=[a11,a21,x31][w1,12w1,22w1,32w2,12w2,22w2,32w3,12w3,22w3,32]z^2=[z_1^2,z_2^2,z_3^2]=[a_1^1,a_2^1,x_3^1]\begin{bmatrix}w_{1,1}^2&w_{1,2}^2&w_{1,3}^2\\w_{2,1}^2&w_{2,2}^2&w_{2,3}^2\\w_{3,1}^2&w_{3,2}^2&w_{3,3}^2\end{bmatrix}

在神经网络进行反向传播，计算梯度时，同样可以利用矩阵运算进行加速，后边我们会详细讲解。

8.3.2为什么GPU适合做矩阵运算

GPU与CPU最大的不同是GPU拥有大量的上千个计算核心，这些核心可以同时处理大量简单的计算任务。而矩阵运算本质就是大量相同的操作（如乘法和加法），非常适合并行化。进行矩阵乘法时，每个结果矩阵的元素可以由不同的GPU核心并行进行计算，彼此并不影响。

GPU最初是为了图像处理而设计的，而图像也是一种矩阵（像素的二维矩阵）。GPU天生就优化了对矩阵、向量的处理能力。另外，随着人工智能的兴起，GPU也专门加强了GPU在人工智能领域的计算能力，从硬件层面做出优化，比如Tensor Core，它就是专门为了矩阵乘法设计的硬件单元。

results matching ""

    No results matching ""