5.3 梯度下降算法
前两节我们讲的例子里,只有w和b两个参数需要找出最优解。并且我们的假设函数是线性的。可以直接让损失函数对w和b求编导,并让偏导数为0,联立方程组来求出让loss最小时w和b的最优解。
但是在深度学习里,对参数求最优解却用的是梯度下降算法。为什么呢?
高维参数空间 深度学习里需要优化的参数非常多,比如对于大语言模型,一般都有几百亿参数,这么多参数联立方程求解是不可能的。
非线性 后边我们会讲到,由于深度学习里引入了激活函数,激活函数是非线性的变化。解方程的方法将非常复杂,以致无法实现。
5.3.1 一元函数求最小值
假设有下边这样一个一元函数,它的函数图像如下:
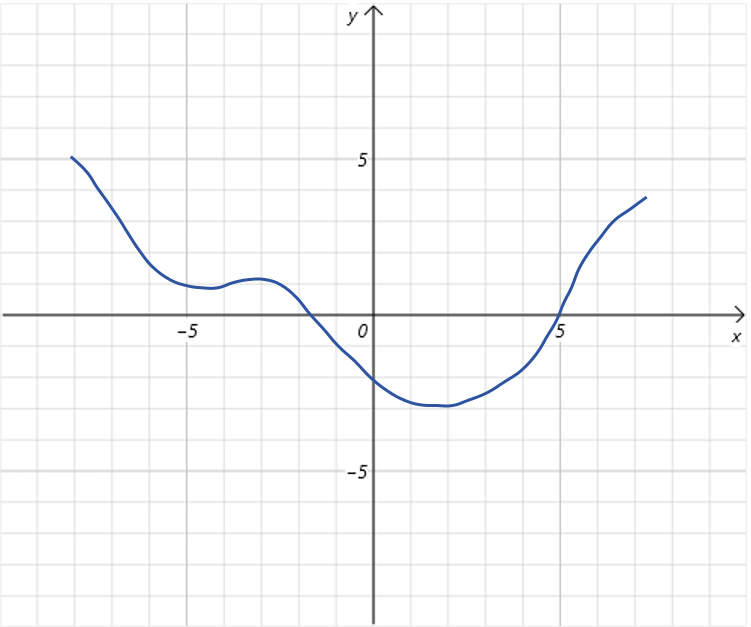
目标是找到能让最小的。首先随机设置的初始值,比如点:
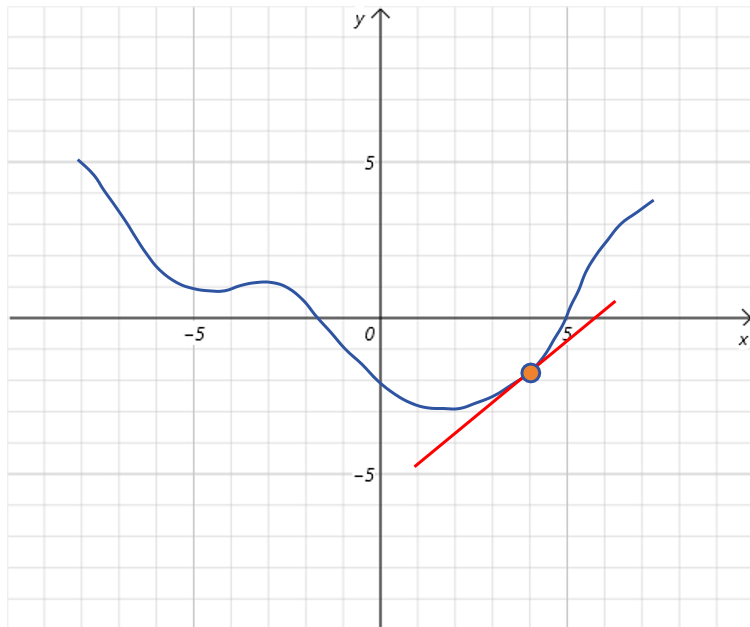
然后我们求出导数,通过观察图像可以看到在点,是大于0的。根据导数的定义,导数大于0,表明当x在处增大时,也就是向右变化时, 是增大的;x在处减小时,也就是向左变化时, 是减小的。
所以根据的正负号,我们就确定了修正的方向。也就是取导数的反方向。如果导数为正,那意味着对做减操作(向左运动)。如果导数为负,那意味着对做加操作(向右运动)。
方向确定后,如何确定移动的步长呢?
直接取负的导数值
有一个简单的做法,就是步长就取导数值的大小。又因为上边说移动方向要和导数方向相反。所以直接的做法就是给加上负的导数值。比如上图中,那么接下来就给加上-1。就从4移动到了3。可以看到它离全局最小点更近了。
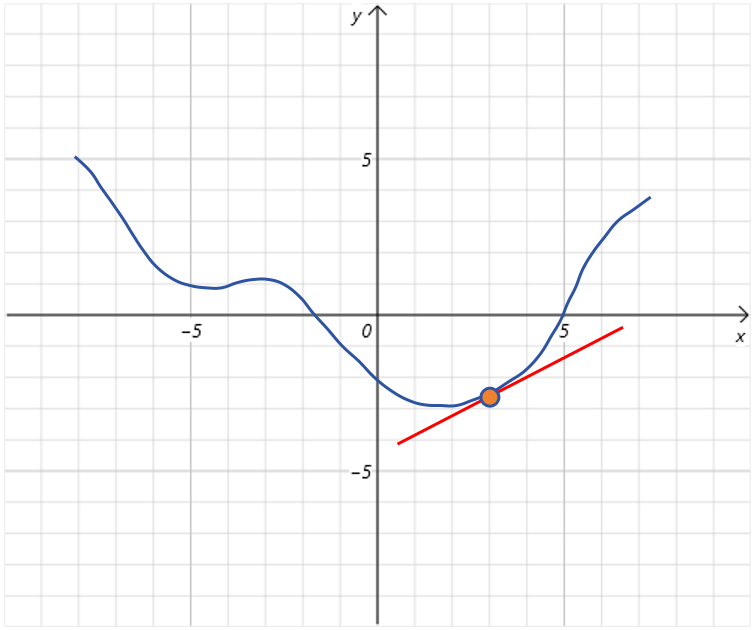
可以看到,在时,的值大概为0.7,比时的导数值小,从图像观察不难发现,随着不断接近全局最低点,曲线也变的平滑,导数值变小。这时我们接着对加上负的导数值,更新为2.3。
根据上边的步骤,我们不断更新的值,而且随着不断接近全局最低点,曲线也变的平滑,导数值变小,每次步长也变小,这有利于我们在全局最低点附近进行精细调整。最终到达全局最低点。
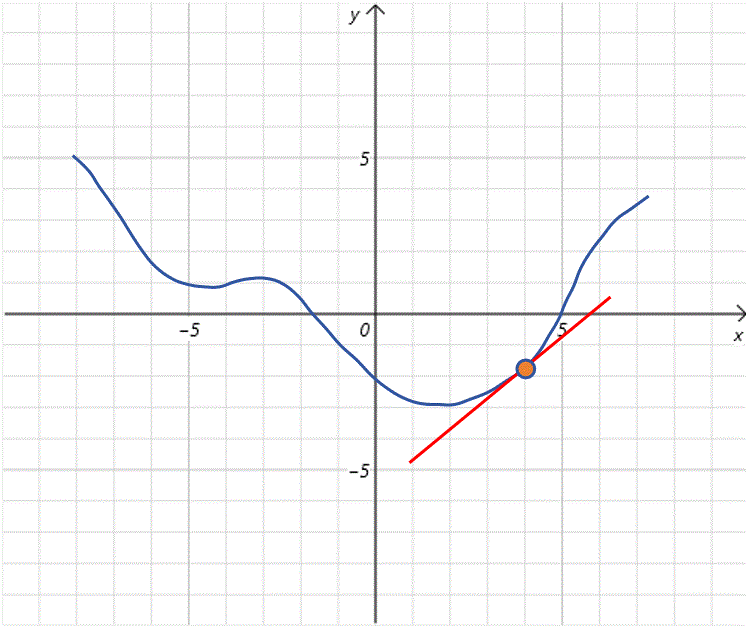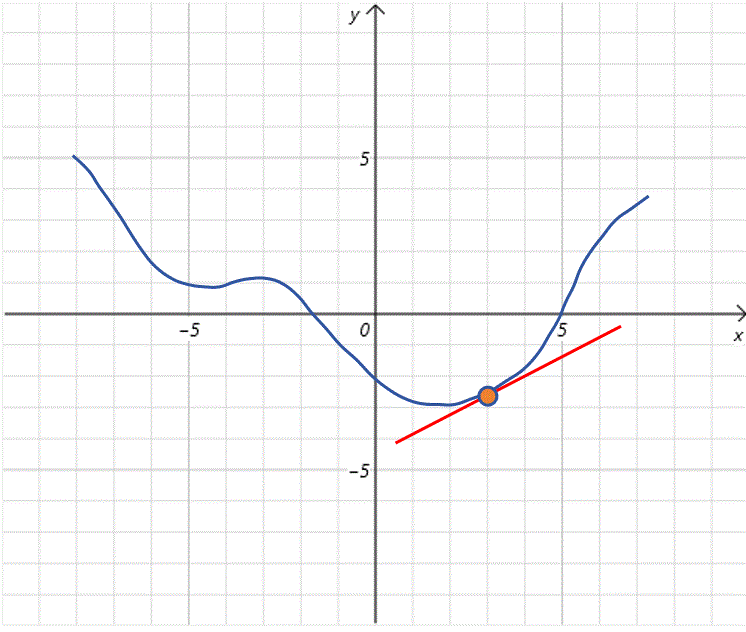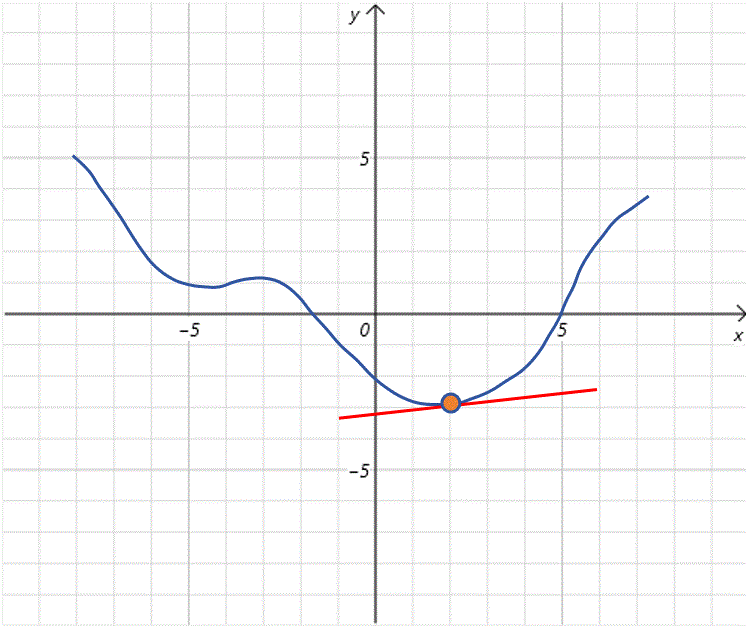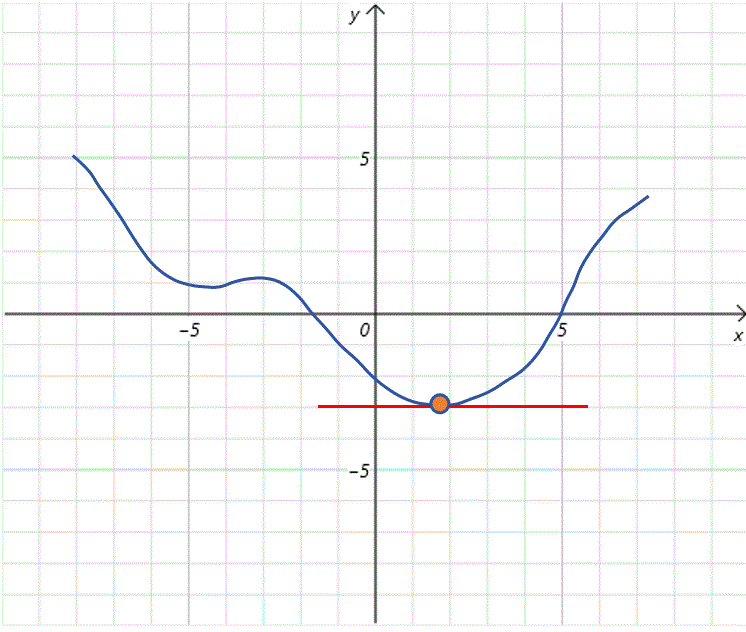
学习率
通过上边的例子,我们可以看到,直接以导数值的大小作为步长看起来不错,但是实际上还需要乘以一个步长的系数。步长系数更正式的名字叫做学习率(Learning Rate)。简写做lr。因为导数值并不是总是那么合适,有时候偏大,导致步长太大,跳过全局最小值。有时候偏小,导致训练过程很慢。这时就可以通过设置学习率来调整。一般情况下,学习率都是小于1的。比如设置为0.001。
参数和超参数
在机器学习领域,在训练过程中由算法调整的变量叫做参数。参数是通过数据学习而来的,不是人为设定的。参数决定了模型如何从输入数据映射到输出。训练好的模型会保存这些参数,以便在预测/推理时使用。比如线性回归里的权重和偏置就是参数。
超参数是模型训练前需要人为设置的变量,它们不会在训练过程中自动学习,而是由人根据实验或者经验设定的。比如学习率就是一个超参数。
5.3.2 多元函数求最小值
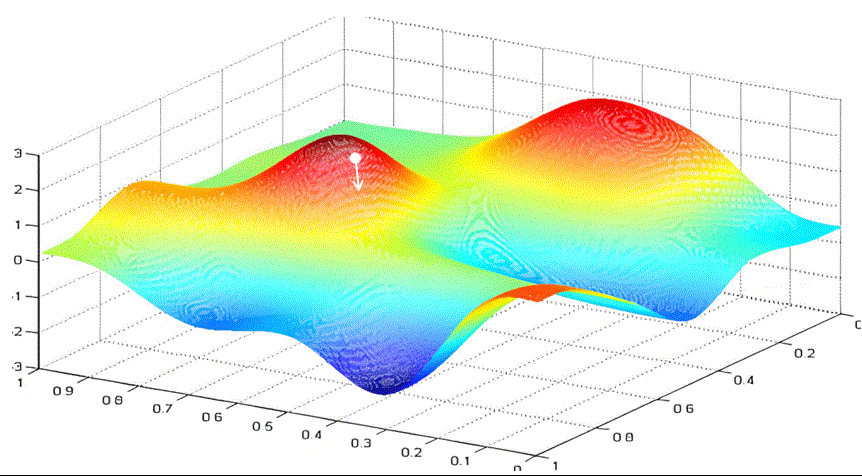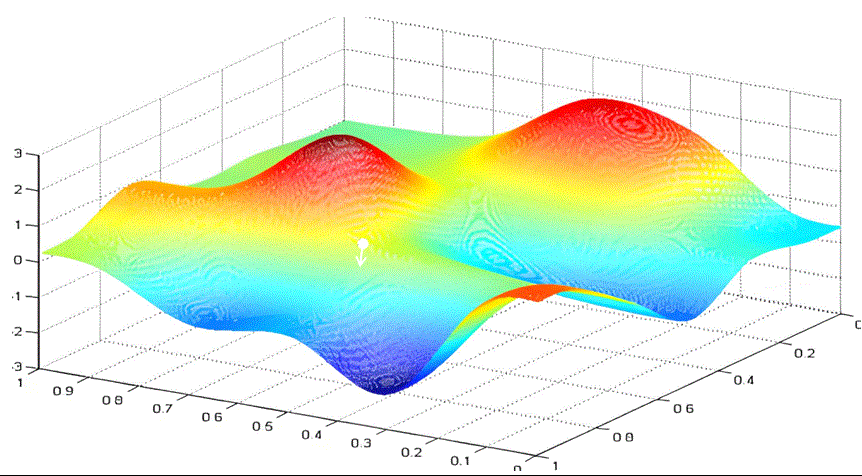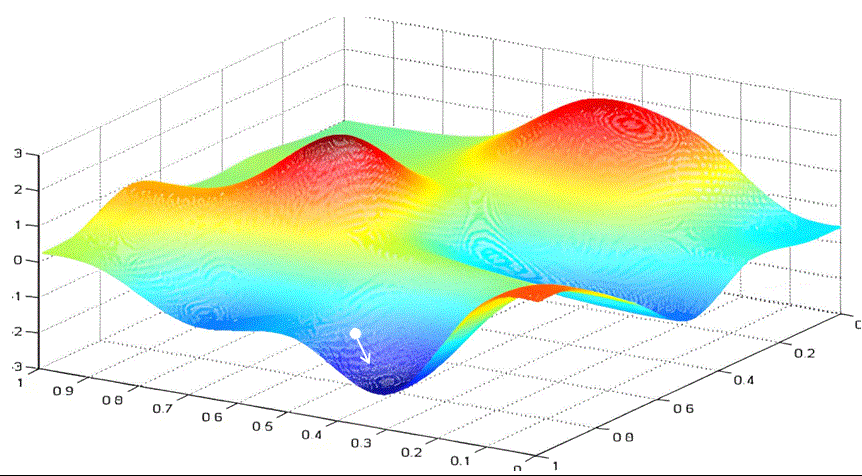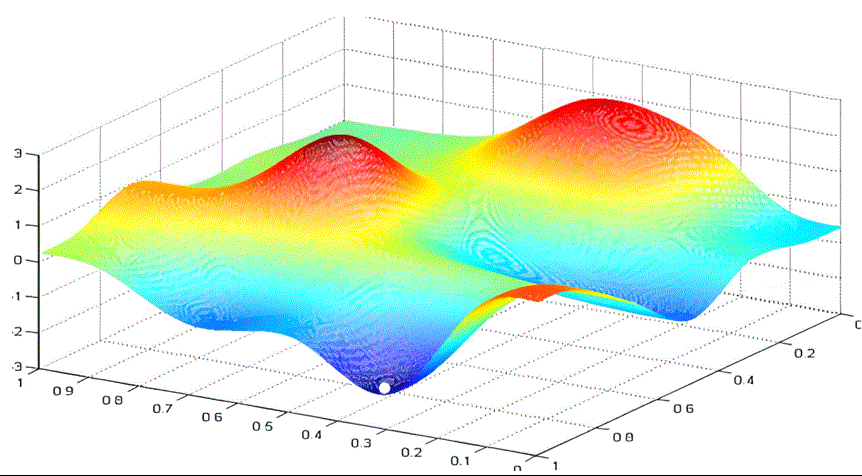
实际情况中,我们都是要优化多个参数。当我们需要优化的参数从一个变为两个时。假设我们要优化参数w和b。以w作为x轴,b作为y轴,loss函数作为z轴。绘制的图像为:
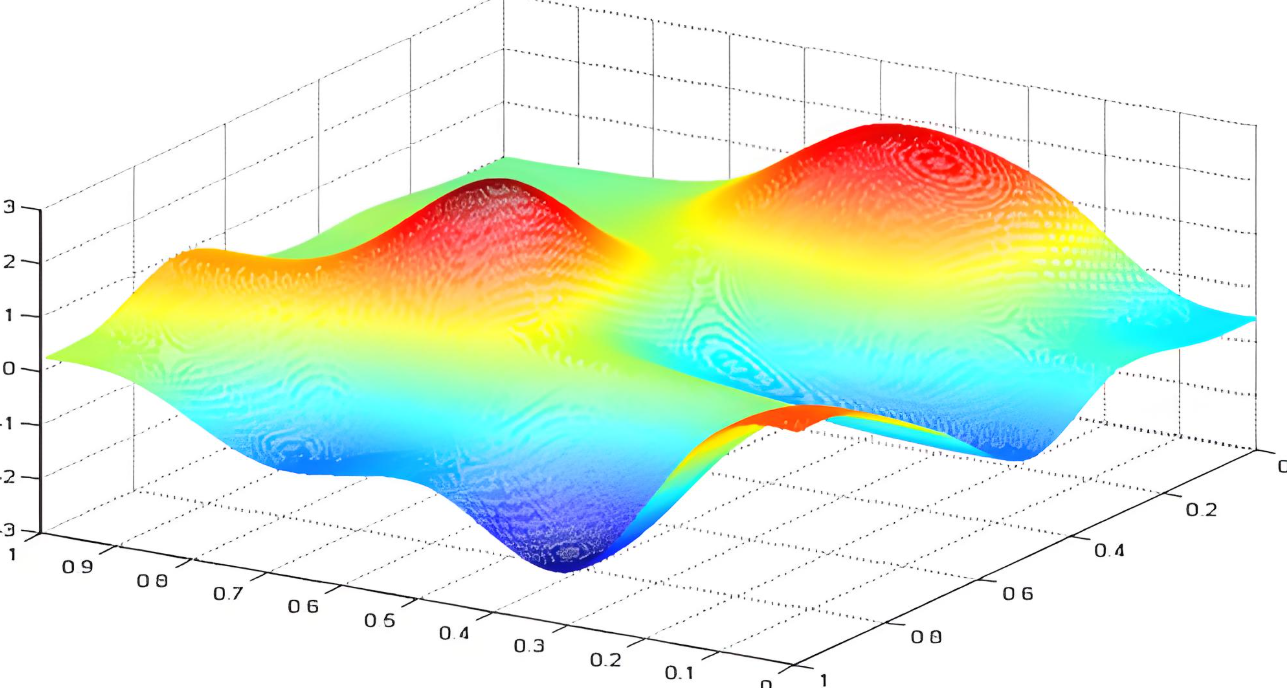
我们的目标是找到loss最小时的w和b。

你可以想象你是一个登山者,被困在一个云雾缭绕的大山里。你想尽快下山,但看不清远处的路。你会怎么选择眼前的路呢?梯度下降的做法是选择沿最陡峭的路向下走一段,然后再观察,再选择最陡峭的路向下。
与一元函数求最小值类似,我们可以给每个参数随机设置初始值。根据梯度的定义我们知道,沿梯度方向函数值增长最快,那么沿着梯度的负方向,函数值就下降最快。所以我们选择沿着梯度的负方向,给梯度值乘以学习率作为步长前进。
这样不断迭代,最终得到loss最小时的w和b。
5.3.3 梯度下降算法的几个要素
初始化
对于每个要优化的参数,随机初始化一个值。
计算梯度
根据当前参数值,对每个参数求偏导,得到梯度值。
迭代更新参数
让当前参数向量沿着梯度负方向,用学习率乘以梯度的值前进。然后再计算梯度。
停止条件
可以设置迭代次数,当到达迭代次数后则停止更新。
或者可以设置loss连续多个迭代不减小,则认为到达loss最小处,停止更新。
5.3.4 损失函数除以样本数
每个参数在每次梯度下降迭代时,都和损失函数的偏导数相关。损失函数不能和样本个数相关。之前我们定义的损失函数是所有样本的label和预测值的误差的平方和。
为了让训练稳定,不同的样本数也有差不多大小的偏导数值。一般在loss函数都会除以计算loss的样本数。
对于回归问题,一般采用的均方误差(Mean Squared Error,MSE)。其公式为:
5.3.5 不用担心鞍点和局部最优解
鞍点
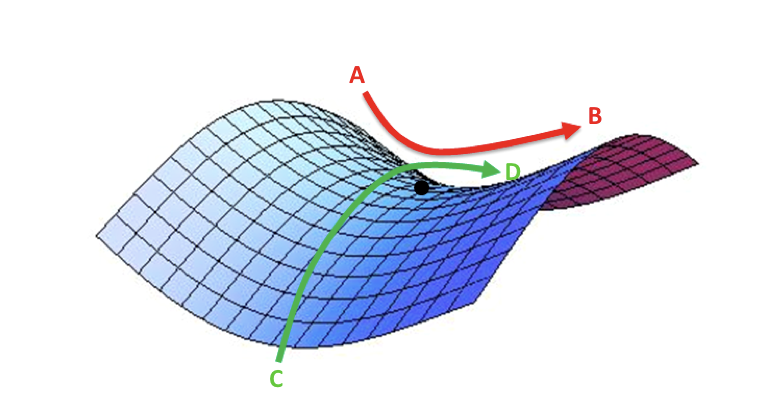
向上图中的点,就称为鞍点,之所以叫做鞍点,因为它像马鞍。沿AB方向鞍点处于最小值,沿CD方向鞍点处于最大值。但是因为实际训练模型时,参数非常大,基本不可能在某一点让每个维度不是最大值就是最小值。所以你不用担心训练过程最终会收敛到鞍点。
另外局部最优解的情况也不用担心,基本上不会遇到。因为训练的参数量非常大,几乎不可能所有参数在某一点同时到达局部最小值。另外后边我们会讲到的带动量的优化算法也会规避陷入局部最优解的情况。带动量的优化算法你可以理解为从山上滚下的小球是带有惯性的,可以帮助它冲过一些小的坑,不会陷入下降过程中的局部小坑中。