8.7梯度消失和梯度爆炸

在上一节里，我们推导了神经网络的每层权重和偏置的梯度计算。我们利用链式求导，从最终的loss值开始，逐层反向计算梯度值。最终导致前边层的梯度值，是很多导数值的连乘。 以上一节3层的神经网络为例，其中第一层权重的梯度值就为：

$\frac{\partial loss}{\partial w^1}={x}^T\delta^1$

我们把$\delta^1$展开就有：

$\frac{\partial loss}{\partial w^1}={x}^T\delta^2(w^2)^T\odot act'(z^1)$

再把$\delta^2$展开就有：

$\frac{\partial loss}{\partial w^1}={x}^T(a^3-y)(w^3)^T\odot act'(z^2)(w^2)^T\odot act'(z^1)$

可以看到第一层权重的梯度值由它后边各层的激活函数的导数值：$act'(z^2),act'(z^1)$，以及后边各层的权重值：$(w^3)^T,(w^2)^T$，一起连乘构成。

上边的例子还只是一个3层的神经网络，如果是100层的神经网络，对于第一层的权重的梯度值，就有99个激活函数的导数值连乘，99个权重值连乘。

很多数的连乘有个问题，就是如果这些数都小于1，比如为0.7，100个0.7的连乘就为2的负16次方，导致梯度非常小，几乎消失，让参数无法更新。如果这些数都大于1，比如都为1.5,100个1.5连乘，结果大概是4的17次方。导致梯度过大，称为梯度爆炸。不论梯度消失还是梯度爆炸，都会让神经网络无法正常训练，特别是对于深度神经网络。

8.7.2 激活函数的选择

上边我们可以看到，在求神经网络中某一层的参数的梯度时，里边会有它后边各层的激活函数的导数值的连乘。

首先我们看一下sigmoid函数的原函数（蓝色）和导函数（红色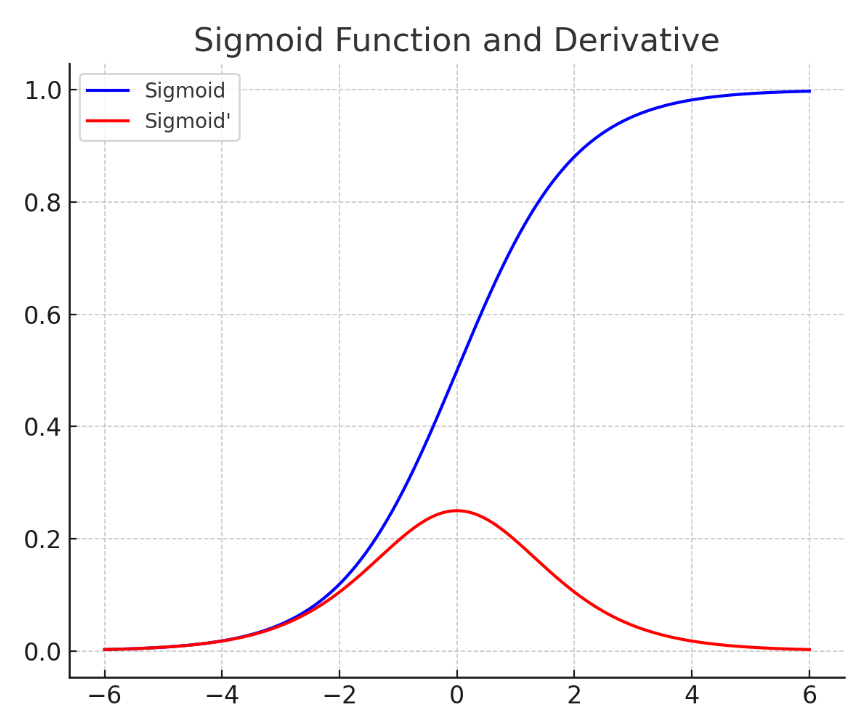）： 可以看到在输入为0时，simgoid的导数取最大值，即使最大值，也只有0.25。如果神经网络中某一层后边还有很多层，在计算该层参数的梯度时，就会连乘很多sigmoid的导数值，取值范围为（0-0.25），这将导致梯度消失，无法正常更新参数。另外还有上一节我们所说的sigmoid函数会导致每一层输出都非负，训练变慢，所以sigmoid函数不适合作为作为隐藏层的激活函数，只适合作为二分类函数最后输出层的激活函数。将最后一层的logits映射到0-1之间，刚好表示结果是正例的概率。

接着我们看一下tanh函数的图像：

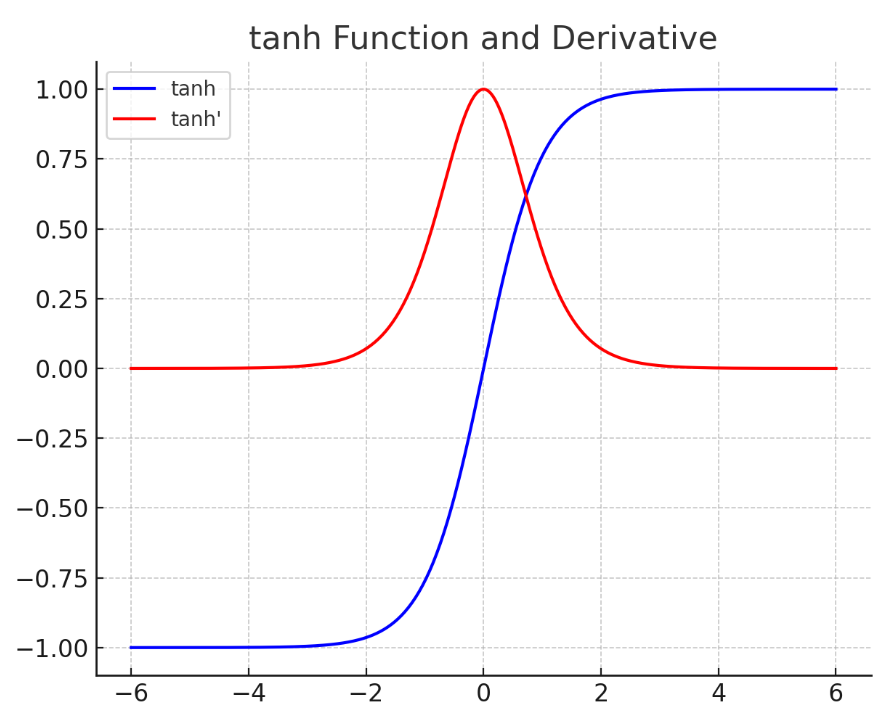
通过看图，我们发现tanh函数的输出有正有负，而且它的导函数取值范围为0-1，也比sigmoid函数要好。但是你会发现当tanh的输入小于-4或者大于4时，梯度就非常接近0了，所以在训练时要非常小心，确保让tanh函数的输入不能偏离0太远。

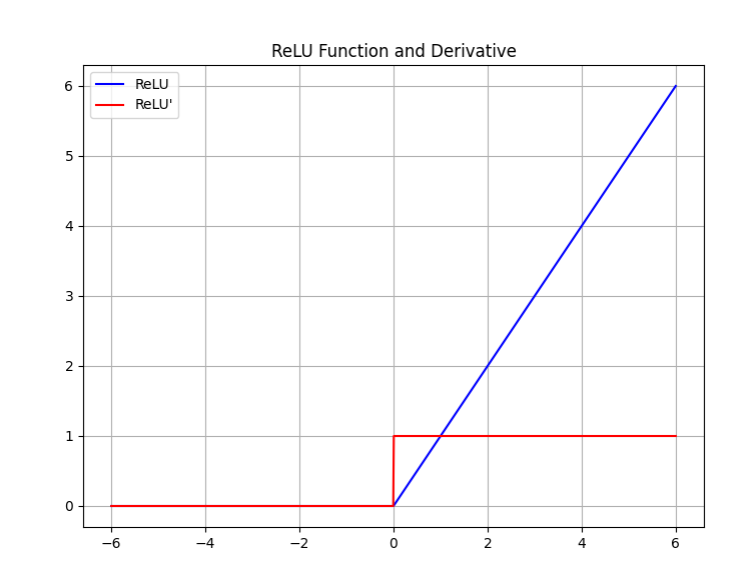
对于ReLU函数而言，只要输入大于0，它的导数值恒等于1，输入小于0，导数值为0，神经元处于抑制状态。所以ReLU更适合用在深度神经网络里。几乎成为深度神经网络默认的激活函数。

8.7.3 参数值的初始化

对于深度神经网络而言，参数的正确初始化也非常重要，因为我们通过前边的例子可以看到，梯度值公式里也有很多权重值相乘。如果权重值初始化为很小的值，或者很大的值，那么也会出现梯度爆炸或者梯度消失的问题。

消除对称性

首先参数初始化一定要随机，如果某一层的神经元的参数都设置为同样的初始值。因为对于同一层的不同神经元，它们的输入是相同的，如果参数也相同，则输出也相同，反向传播的梯度也相同，每次参数更新后的值也一样，多个神经元就失去了差异性。所以初始化参数时一定要随机，来消除神经元之间的对称性。

控制方差

一般神经网络的输入都经过了标准化，输入都是均值为0，方差为1的变量。我们可以通过随机生成均值为0，方差为1的参数值来初始化网络参数。但是有个问题，就是我们希望神经网络正向传播时，每一层输出的方差不变，保持稳定。但是神经网络每一层都是每个输入和对应权重乘积的累加，有n个输入，就是n个值的累加。导致方差变为n。另外考虑因为采用ReLU激活函数，导致大约一半的输入为0，所以方差应该修正为$\frac{n}{2}$，为了保持方差不变，对初始化权重进行调整，将权重初始化为均值为0，标准差为$\sqrt{\frac{2}{n}}$的随机变量。其中n为当前层输入的数量。这是用正态分布初始化参数的方法，也有用平均分布来初始化权重的方法。对于偏置，默认初始化为全零即可。不用担心，在使用PyTorch定义神经网络层时，它会自动帮你初始化好参数。

8.7.4其他方法

除了选择合适的激活函数，恰当的初始化参数外，还有其他一些缓解深度神经网络训练时出现梯度消失或者梯度爆炸的方法，比如后边我们会讲到的批量归一化方法，或者残差连接这样的网络结构设计。