9.3动量梯度下降

今天我们来学习一种对梯度下降算法改进的算法：动量梯度下降算法（Momentum Gradient Descent）。它可以让训练时稳定并且迅速。

9.3.1梯度下降的问题

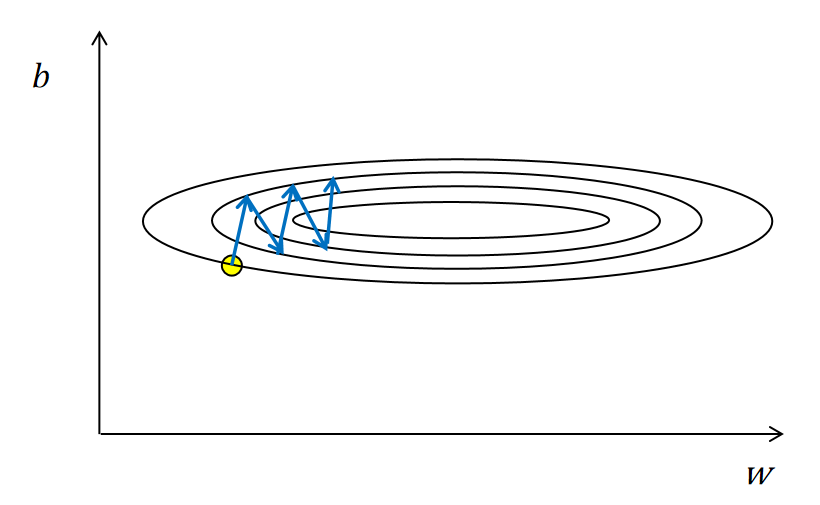
如上图中有两个需要优化的参数，横轴的w和纵轴的b。图中的椭圆是损失函数的等高线。黄色的点为初始化的w，b的位置。然后逐步计算loss函数对w和b的偏导数，生成梯度值。按照梯度的反方向更新参数。有一个问题是，神经网络的参数很多，训练时，有的参数的梯度值很大，有的很小。在接近最优点时会产生震荡，如上图所示，沿纵轴b参数的方向产生了震荡。这样训练下去永远到达不了最优点。

梯度下降还有一个问题，当某一参数有局部最优解时，也就是loss对这个参数的偏导数在某一个很小的局部接近0。这时，传统的梯度下降算法对这个参数的更新就非常慢，停滞不前。

9.3.2动量梯度下降

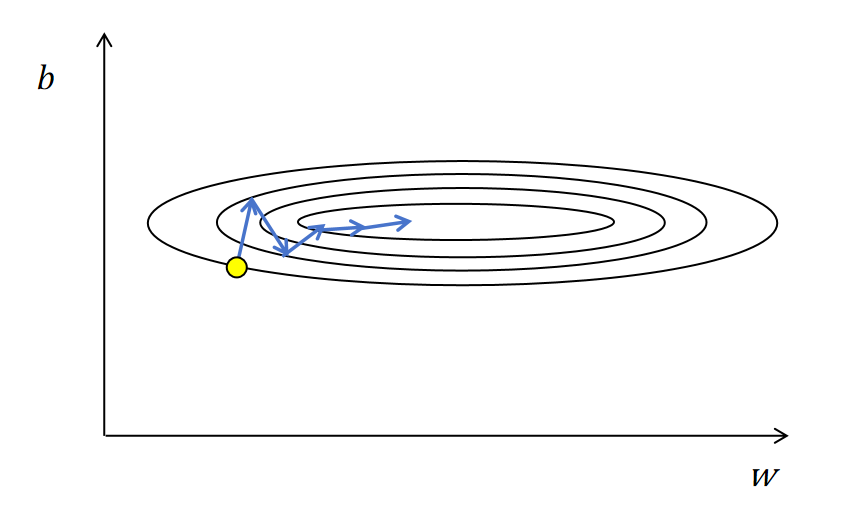
动量梯度下降的做法是每次不用当前每个参数的梯度值来更新参数，而是用梯度值的指数加权平均来更新参数。它可以很好的解决上边说的梯度下降的两个问题。 训练震荡 可以看上图中训练震荡过程中，b的梯度在训练过程中，是正负不断变化，进行震荡的。经过指数加权平均，正负可以部分抵消。减小了模型训练过程的震荡，使loss函数可以降到最低。 局部最优 因为指数加权平均会考虑历史的梯度值，不会因为当前的梯度值为0而为零，所以在局部最优点，也就是梯度值为0时，它的更新梯度值还是沿着历史方向继续更新。不会陷在局部最优点。

你可以形象的理解，一个小球从山顶滚下来，因为有惯性（动量），它会逐渐克服震荡，沿着一个方向滚动，而且遇到一些小的沟壑（局部最优），也会靠惯性冲过去，最终到达底部（最优解）。

一句话来说动量梯度下降的作用就是抑制震荡，惯性加速。

9.3.3动量梯度的更新过程

以对w参数的更新为例，首先计算w的梯度：

$g_w=\frac{\partial loss}{\partial w}$

我们定义变量$V_w$, 表示$g_w$的指数加权平均值，每个batch按照下边的公式更新自身值：

$V_w=\beta V_w+(1-\beta)g_w$

更新w参数, $lr$是学习率：

$w=w-lrV_w$

可以看到在训练过程中，对于参数w，一直需要保存一个指数加权平均值$V_w$。另外$\beta$ 的取值一般为0.9。