3.6 偏导数
3.6.1 一元函数的导数
之前我们讲过一元函数的导数,函数在自变量某一点x0的导数,表示当自变量的变化量△x→0时,因变量关于自变量的变化率。
f′(x0)=lim△x→0△x△y=lim△x→0△xf(x0+△x)−f(x0)
3.6.2 多元函数的偏导数
对于多元函数,比如:
我们想要求函数在点(x0,y0)处的导数时,情况就变得复杂。因为对于一元函数而言,自变量只有一个,但是对多元函数,自变量有两个。为了简化我们的研究,每次可以只让自变量里的一个变量变化,而其他变量保持不变,这时对多元函数的求导,就转化为对一元函数的求导了,我们把这种导数,叫做偏导数。
比如对于上边自变量包含x和y的多元函数,在点(x0,y0)处,固定y=y0,对x求偏导:
fx(x0,y0)=lim△x→0△x△zx=lim△x→0△xf(x0+△x,y0)−f(x0,y0)
在点(x0,y0)处,固定x=x0,对y求偏导:
fy(x0,y0)=lim△y→0△y△zy=lim△y→0△yf(x0,y0+△y)−f(x0,y0)
偏导数也可以用另一种形式表示,比如z对x求偏导,可以表示为:
∂x∂z
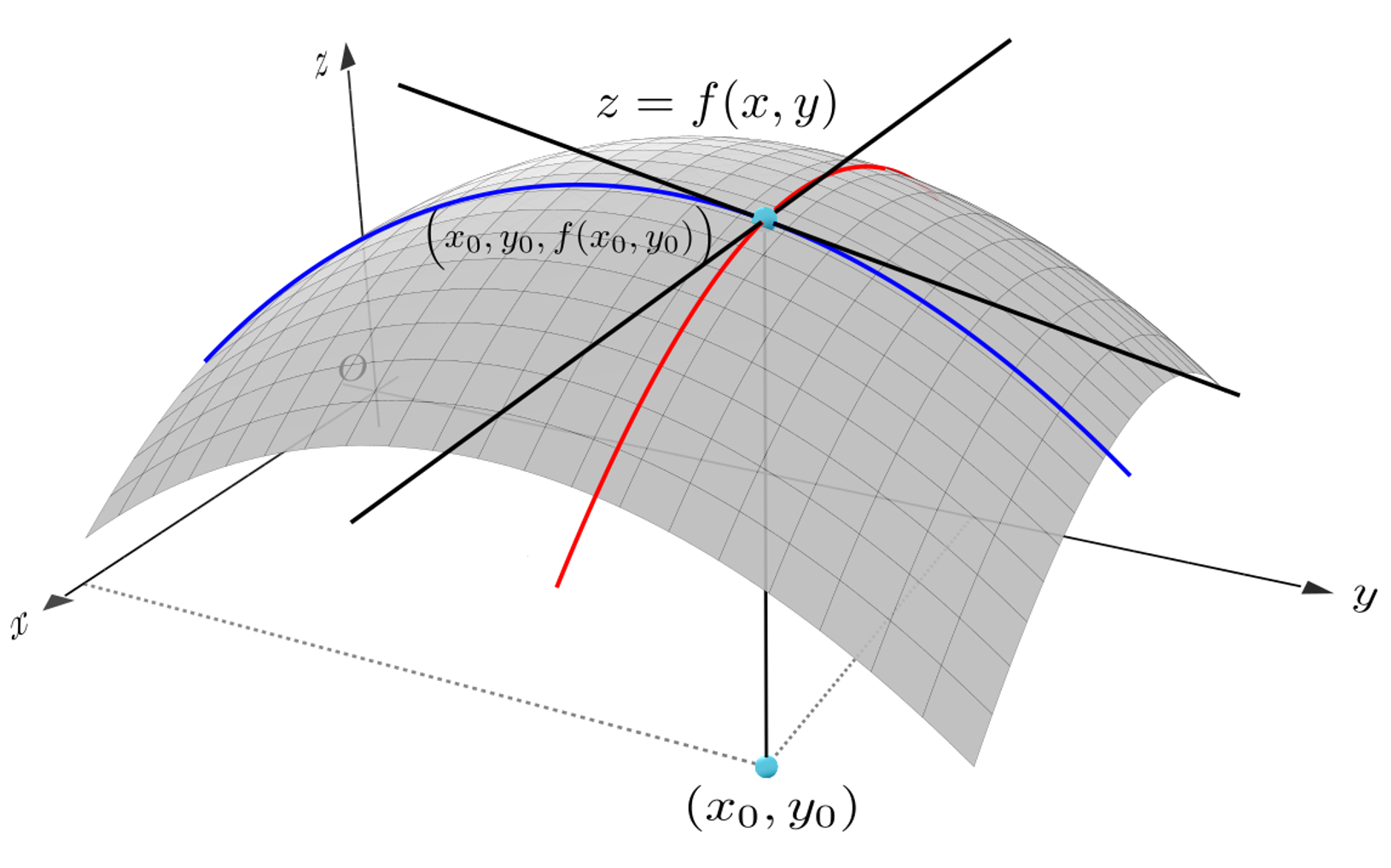
3.6.2 偏导数的几何意义
根据上图可以看出,多元函数的偏导数也和一元函数的导数一样,都是表示切线斜率。
对于偏导数fx(x0,y0)表示的是平面y=y0与曲面z=f(x,y)的交线在x=x0处,z对于x的变化率。
对于偏导数fy(x0,y0)表示的是平面x=x0与曲面z=f(x,y)的交线在y=y0处,z对于y的变化率。